Deformation forecasting model and its modeling method of super high arch dams during initial operation periods
-
摘要: 针对特高拱坝运行初期温度场的非稳定性和时效的非单调增长性,发展变形监测和预报模型,并提出构建方法。通过主成分上的分层聚类法选取代表性温度测点,将其实测值作为温度变量,引入包含徐变及其恢复项的时效变量表达式,论证其表达谷幅变形的能力。进而考虑库水位、实测温度、组合时效等变量,应用增强回归树方法提出特高拱坝运行初期变形监测和预报模型,并通过后向消减变量建立优化模型。分析各变量对变形的边际效应,得出相对影响,借助部分依赖图,辨识变量间相关关系及其对坝体变形的影响规律,揭示变形机制。将该模型应用于某特高拱坝,验证该模型的可行性和有效性;并将结果与支持向量机、多元回归模型进行对比分析,得出该模型具有显著的优越性。Abstract: The dam temperature field has not been stabilized, and the time dependent effect does not increase non-monotonously for super high arch dams during initial operation period. Therefore a special deformation monitoring and forecasting model was developed, and its modeling method was proposed in the study. The key temperature measurement points were chosen by the hierarchical clustering on principal component method, and the corresponding time series were inputted as thermal predictors. The combined time dependent effect, including creep and its restoration, was introduced as time dependent deformation. This time dependent effect was employed to validate its characterization for the valley contraction deformation. Considering the predictor variables such as reservoir water level, adopted measured temperatures, estimated time dependent effect, the simple boosted regression tree (BRT) based dam deformation prediction model was constructed. Through the backward elimination method, a simplified BRT (SBRT) model only including major predictors was obtained. The marginal effects of variables on deformation were analyzed, and the relative influences can be quantitatively analyzed. With the help of partial dependence plot, the correlations among variables and the influences of variables on deformation can be explored, and the deformation mechanism can be revealed. The model was applied to a super high arch dam, and the case study verified the feasibility of the model. The results were compared with those by the support vector machine model and the traditional multiple regression models, which shows the superiority of the developed model.
-
多座200~300 m级特高拱坝蓄水后短期内均监测到上下游谷幅持续收缩,超出了已有工程经验和规律认知[1-2]。如当水库蓄水并水位长时间处于540~560 m高程时,溪洛渡拱坝向上游变形,并表现出非线性和显著时效特征,蓄水完成后谷幅并未收敛,影响拱坝运行初期变形性态。除谷幅变形外,运行初期库水温垂直分层、水泥持续水化导致坝体温度场仍处于非稳定阶段。可见,运行初期高拱坝处于非稳定、非线性的环境和条件下。同时,根据国际大坝委员会的统计资料,运行初期失事大坝超总失事大坝数的一半。如Malpasset拱坝蓄水造成坝基岩体非均匀大变形、坝体溃决,Vajont拱坝蓄水诱发库岸滑坡,库水翻坝而过、大坝失事,两座拱坝从蓄水到发生事故分别只经过了5年和3年[3-4]。可见,建立科学的运行初期安全监测和预报模型,对掌握大坝安全状态、防患于未然意义重大。
变形是监测大坝安全状况的最主要效应量[5-6]。传统统计模型(Hydrostatic Season Time,HST)应用最广泛,但只适用于时效不显著、温度场稳定的运行期[5]。基于实测温度值的模型(Hydrostatic Temperature Time,HTT)采用代表性的温度测点温变作为温度变量,能在一定程度上弥补HST模型的不足[6]。多元回归模型假设变量间独立,效应量是各变量分量的线性叠加,通过变量分离判断各变量对效应量的影响。当变量间多重共线性时,模型精度差。基于数据的非参数方法如神经网络、支持向量机(Support Vector Machines,SVM)能克服变量间共线性的影响,可建立高精度的非线性模型,在近30年得到了大量应用[7-8]。但这些方法也存在难以解释大坝性态的缺陷。增强回归树(Boosted Regression Trees,BRT)方法除有非参数方法的优点外,还能在运算过程中随机抽取数据分析变量对效应量的影响,从而为安全监测和预报模型提供了新途径[9]。
本文研究特高拱坝运行初期变形监测预报模型。通过基于主成分的分层聚类法(Hierarchical Clustering on Principal Components,HCPC)选取代表性温度测点,将其测值作为温度变量;引入包含徐变及其恢复项的时效变量表达式,论证其表达谷幅变形的能力;进而考虑库水位、实测温度、组合时效等变量,应用增强回归树方法提出特高拱坝运行初期变形监测和预报模型,并通过后向消减变量建立优化模型(Simple BRT,SBRT);采用相对影响(Relative Influence, IR)表示各变量对变形的影响,并借助部分依赖图(Partial Dependence Plot,PDP)探寻变量间相关关系及其对坝体变形的影响规律。将该模型应用于某特高拱坝,并将结果与SVM,HST及HTT模型对比分析,验证模型的可靠性和优越性。
1. 监测预报模型
坝体温度变形在拱坝总变形中占较大比重。从力学观点看,温度变形与温度变化呈线性关系,温度变形分量应选择温度计测值作为因子[5]。当坝体和边界设置足够数量的温度计并连续观测时,实测值足以描绘坝体变温场。此时,温度变形分量δT可表示为:
$$ {{\delta} _T} = {b_i}\sum\limits_{i = 1}^{N} {{T_i}} $$ (1) 式中:bi为待定系数;Ti为测点的温度值;N为选用温度计的数量。
时效是运行初期变形的显著特征,其特点是蓄水后急剧变化,而后随运行时间的增长逐步稳定。时效包括刚固地基上坝体徐变、完整岩体徐变及岩体裂隙节理塑性变形等。同时,相关研究也表明,坝体和岩体的徐变在卸荷后有一定的恢复[5, 10]。
徐变和塑性变形引发的时效变形δθ是随时间单调增加的函数,用一阶衰减微分方程的解来描述[5]:
$$ {\delta _{\rm {\theta}} }{\rm{ = }}c\left( {1 - \exp ( - \gamma \theta )} \right) $$ (2) 式中:c,γ均是待定常数;θ=t/100,t为观测日至始测日的天数。
当库水位呈周期性变化时,徐变恢复项δr可表示为[5]:
$$ {\delta _{\rm {r}}}{\rm{ = }}\sum\limits_{i = 1}^{\rm{2}} {\left({d_i}\sin \frac{{2{\text{π}}it}}{{365}}{\rm{ + }}{f_i}\cos \frac{{2{\text{π}}it}}{{365}}\right)} $$ (3) 式中:di,fi均是待定常数,i=1~2,这里取1。
综合式(1)~(3),并考虑水压变形分量可得到高拱坝蓄水后运行初期的变形预报模型为:
$$\delta {\rm{ = }}\sum\limits_{i = 1}^4 {{a_i}{H_i}} + \sum\limits_{i = 1}^N {{b_i}{T_i}} + c\exp ( - \gamma t) + d\sin \frac{{2{\text{π}}t}}{{365}}{\rm{ + }}f\cos \frac{{2{\text{π}}t}}{{365}}{\rm{ + }}g$$ (4) 式中:H为水库水深;g为待定常数。
2. SBRT的构建及实现方法
2.1 基于HCPC的温度因子选取
HTT模型可显著提高复杂温度条件时的模型精度[6]。但对于特高拱坝,埋设的温度计数量众多,如直接选取全部的库水温、坝体温度等实测数据,会引起过多冗余变量和多重共线性,降低模型的鲁棒性。采用HCPC法,依据各点测值的变化规律,将测点分为不同的组,并选取各组中典型测点的温度测值作为模型的温度变量。
PCA的基本原理可参考文献[11]。当PCA和分层聚类均采用欧氏距离度量时,可融合得到HCPC法,从而更好地描述变量间的关系。对于数据集XKI(K为变量个数,I为观测数),PCA的核心思想是采用S个(S<K)不相关的主成分表征原始数据集,这些主成分反映了原始数据集中多变量蕴含信息的本质,其余的主成分则可认为是噪音。在前S个主成分上进行分层聚类,可以获得比在原始变量上聚类更稳健的结果。可见,PCA也是一种去噪方法,可作为聚类分析的预处理步骤。分层聚类基于PCA和多维方差,采用Ward准则作为聚集方法。该准则基于Huygens定理,分解组间、组内方差得到总方差:
$$\sum\limits_{k = 1}^K {\sum\limits_{q = 1}^Q {\sum\limits_{i = 1}^{{I_q}} {{{\left( {{x_{iqk}} - {{\bar x}_k}} \right)}^2}} } } = \sum\limits_{k = 1}^K {\sum\limits_{q = 1}^Q {{I_q}{{\left( {{{\bar x}_{qk}} - {{\bar x}_k}} \right)}^2}} } + \sum\limits_{k = 1}^K {\sum\limits_{q = 1}^Q {\sum\limits_{i = 1}^{{I_q}} {{{\left( {{x_{iqk}} - {{\bar x}_{qk}}} \right)}^2}} } } $$ (5) 式中:xiqk为第q组的变量i在观测点k的值;
${\bar x_k}$ 为各变量在观测点k的平均值;${\bar x_{qk}}$ 为第q组内各变量在观测点k的平均值;Iq为第q组内的观测数。组内方差表征了组内变量的同质性,Ward准则在聚类时使每个步骤中组内方差增长最小,即组间方差减少最小。确定分组数是聚类分析的核心问题。分层聚类本质是一种嵌套分区,最底层上每个变量均是一个小组,最顶层上所有变量都归属同一个大组。可根据组内方差的增长情况判断最优的聚类分组结果。当分组数从(Q−1)到Q时的组间方差的增加值ΔQ远大于从Q到(Q+1)时的增加值Δ(Q+1)时,最优分组数为Q组。可采用两种方法来获得最终的聚类分区,一是保持分层聚类得到的Q个分组;一是借助K-means算法,将分层聚类结果作为初始分区,通过若干次迭代获得改进的分区结果,迭代过程中通过组间方差的比值判断。通常,初始分区不会被完全替换,而是得以改进。
变量的分层聚类分区结果可表示在主成分映射图上或树形图上。
2.2 基于SBRT的模型构建
BRT综合了回归树和Boosting增强算法。通过回归树拟合一组单模型,并使用增强算法组合回归树的输出以计算总体预测值。BRT的核心在于,每一棵树是从之前所有树的残差中学习的,利用残差梯度来优化回归树的集成过程。
回归树基于类似样本组中训练数据的递归划分,将特征空间划分为不同的区域,给每个区域以相应的常数,通过将数据划分至不同区域进而得到预测值,其输出是每个组内观察的输出变量的平均值。回归树每次生成树的子节点只有2个,即递归地二分每个特征,采取平方误差作为评价指标,在每一步选择一个最好的特征来分裂。这样,将输入空间即特征空间划分为有限个单元,并对应以相应的数值。当考虑多个变量时,计算每个变量的最佳节点,并选择导致误差减小最大的节点。因为一个节点中弱相关变量的误差减少一般低于强相关变量,所以算法自动舍弃不相关的变量。Boosting算法基于训练数据生成的多个简单模型,通过集合中的每个模型的输出的加权和实现整体预测。算法的基本思想是让每个学习者适应前一个集合的残差。
回归树和平方误差损失函数时,原始增强算法的主要步骤可总结如下。
用观测的平均值进行预测:
$${F_{\rm{0}}}\left( {{X^j}} \right) = {f_0}\left( {{X^j}} \right) = {\bar y_i}$$ (6) 对于m=1,2,···,M,计算训练集的误差:
$${\tilde y_i} = {y_i} - {F_{m - 1}}\left( {x_j^i} \right)$$ (7) 绘制训练集的随机子样Sm;考虑Sm,基于前一个集合的残差拟合新的回归树:
$$\begin{array}{*{20}{c}} {{{\tilde y}_i} \approx {f_m}\left( {{X^j}} \right),}&{i \in {S_m}} \end{array}$$ (8) 更新集合:
$${F_m}\left( {{X^j}} \right) \Leftarrow {F_{m - 1}}\left( {{X^j}} \right) + {f_m}\left( {{X^j}} \right)$$ (9) Fm是最终的模型。通常认为该过程易于过拟合,因为训练误差随迭代而减小。为了克服这一问题,添加正则化参数
$\upsilon \in \left( {{\rm{0,1}}} \right)$ ,从而上一步可以变换为:$${F_m}\left( {{X^j}} \right) \Leftarrow {F_{m - 1}}\left( {{X^j}} \right) + \upsilon \cdot {f_m}\left( {{X^j}} \right)$$ (10) 已有研究表明,相对较小的正则化参数(υ<0.1)可极大提高泛化能力[9]。通常设较小的正则化参数并考虑多个树,使得误差稳定。随后,使用交叉验证来优化参数。本研究中设定υ=0.001,树的数量上限为10 000。应用十重交叉验证来确定最终集合中树的数量,构建BRT模型。在此基础上,通过后向消减影响较小的变量,优化建立更为稳健的SBRT模型。
2.3 变量相对影响大小的确定
训练过程主要变量被频繁地选取,次要变量被舍弃,变量x
j的IR与它们出现的频率成比例。 $$ I_j^2 = \sum\limits_{{x_j}} {I_t^2} $$ (11) 式中:Ij为变量xj的相对影响。
$I_t^2$ 是在这一节点上xj的改进。变量xj的IR是Boosting算法所有生成树的平均值。根据IR值来确定变量和效应量的关联性。2.4 重要变量的部分依赖图
使用PDP通过边际效应识别变量-效应量间的关系。
${X^j}$ 为变量,在其范围内定义一组等间距值,即${X^j} = x_k^j$ 。对于这些值,模型效应量的平均值计算如下:$$\bar F\left( {x_k^j} \right) = \frac{1}{N}\sum\limits_{i = 1}^N {F\left( {x_i^j,x_i^{jc}} \right)} $$ (12) 式中:
$x_i^{jc}$ 是所有变量而非${X^j}$ 的值。2.5 监测预报模型的实现流程和性能评价
基于SBRT方法的特高拱坝运行初期变形监测和预报模型的实现步骤如下:①监测数据预处理;②基于HCPC选取典型实测温度变量,确定合适的时效变形表达式;③构建BRT模型,通过后向消减建立SBRT模型;④计算各变量的IR,生成部分PDP,判定变量对效应量的影响。
通过平均绝对误差(Mean Absolute Error, eMAE)分析模型的拟合效果,定义如下:
$${e_{{\rm{MAE}}}}{\rm{ = }}\frac{{\displaystyle\sum\limits_{i = 1}^N {\left| {{y_i} - F\left( {x_k^j} \right)} \right|} }}{N}$$ (13) 式中:N为训练或者预测样本集的大小;yi为实测的监测效应量值;F(x)为预测值。
3. 工程应用
3.1 工程和监测概况
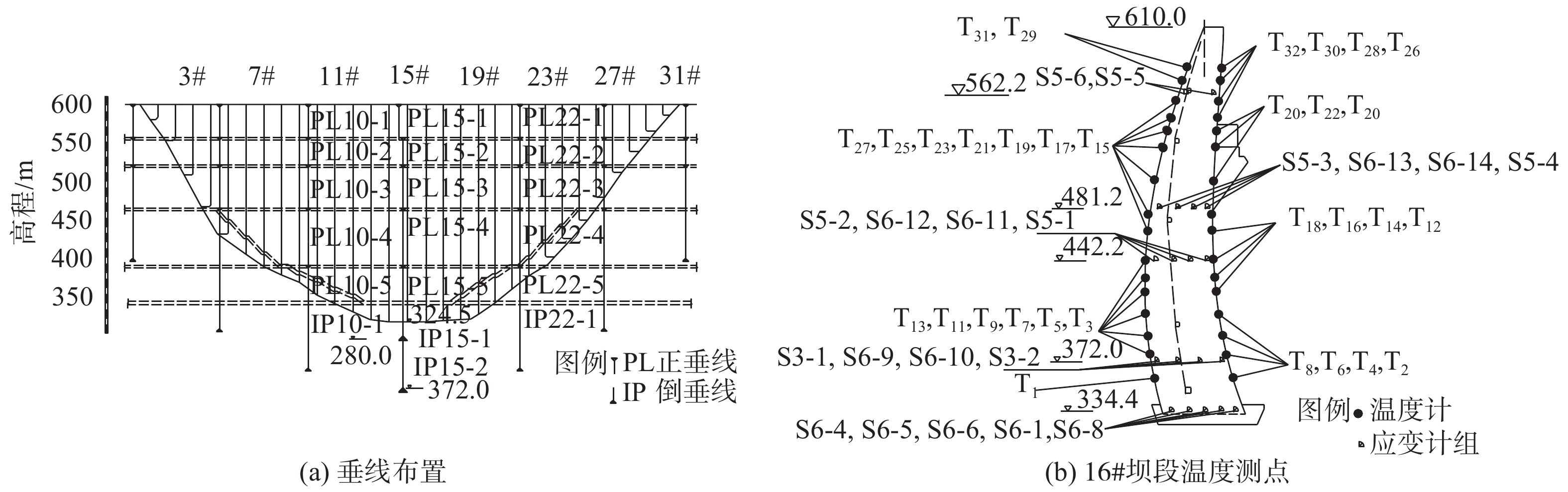
某混凝土双曲拱坝坝顶高程610.0 m,建基面高程324.5 m,共31个坝段。水库的正常蓄水位、死水位和汛限水位分别为600.0,540.0和560.0 m,水库具有年调节能力。坝体变形布设坝体垂线监测系统和坝后桥外观大地测量两个监测系统。在坝体典型高程上、下游面各布置1支温度计观测环境温度,内部则采用应变计组的测温传感器观测内部温度。15#坝段垂线和16#坝段的温度测点布置如图1,其中,T为温度计,S(k-i)表示k向应变计第i个测点。
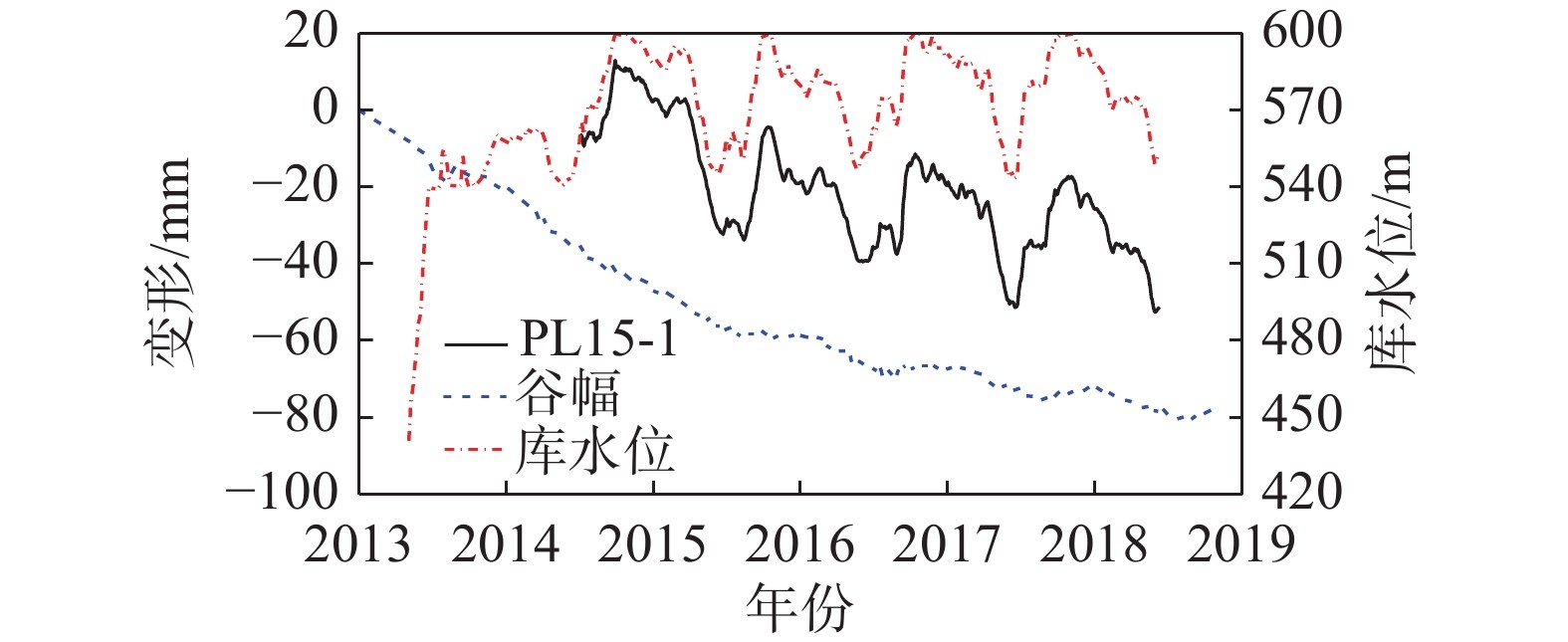
2013年5月4日,导流底孔下闸水库开始蓄水(图2)。2014年3月6日,大坝完成浇筑。2014年9月28日,第一次蓄至正常蓄水位。当前谷幅出现较大变形且仍未稳定(图2)。通过比较15#坝段相同高程两套变形监测系统测值,发现两者在顺河向变位观测值存在3 mm的差值,但变化规律一致[12]。
3.2 变量选取
库水位、温度为每日平均测值,垂线测点的监测频次为2~3 d/次。分析的PL15-1的时间序列为2014年6月—2018年6月,在此期间坝体经历了4次完整的加载和卸荷过程。
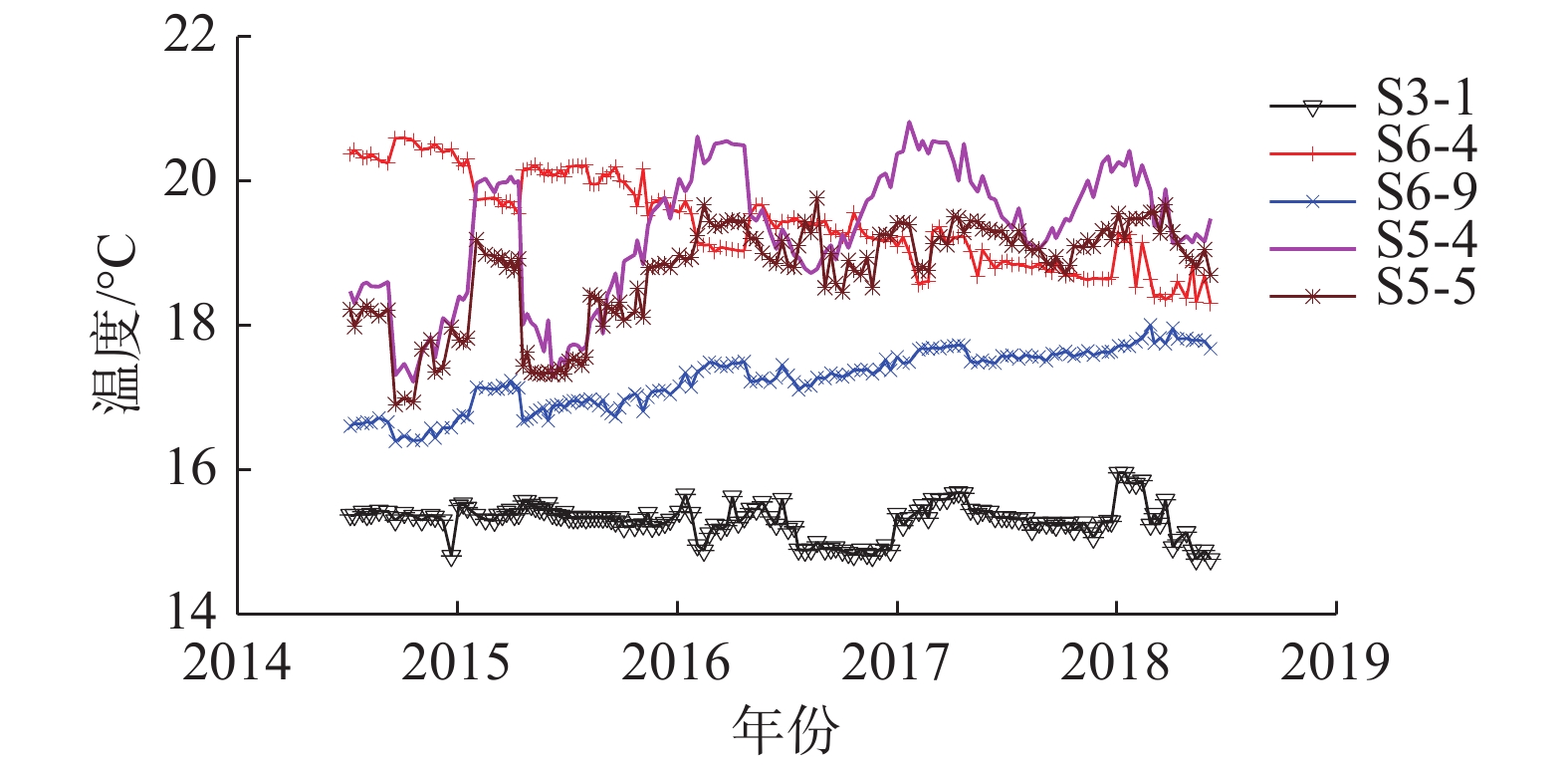
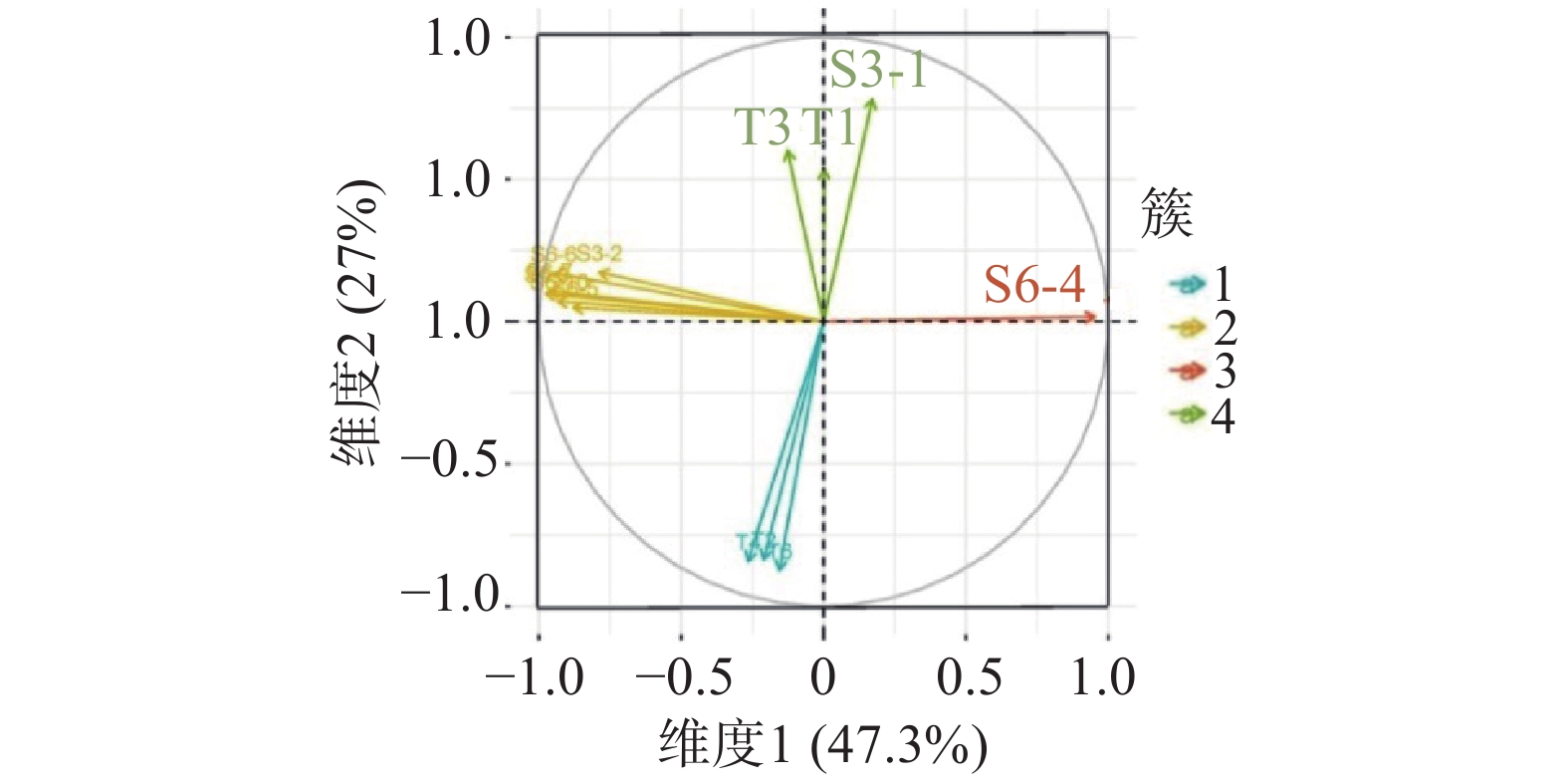
温度变量采用16#坝段实测温度作为相邻15#坝段的数据。典型测点实测温度过程如图3。可看出,高高程内部测点温度仍有上升的趋势,而坝基内部测点温度变化跟位置有关。应用HCPC法,以PL15-5段为例,根据Ward准则对温度测点聚类,最终确定为4类(图4),选取的该垂线段的温度计列于表1,同理,其余垂线段的结果也列于表1。高高程垂线测点模型构建还应考虑其下所有典型温度测点。
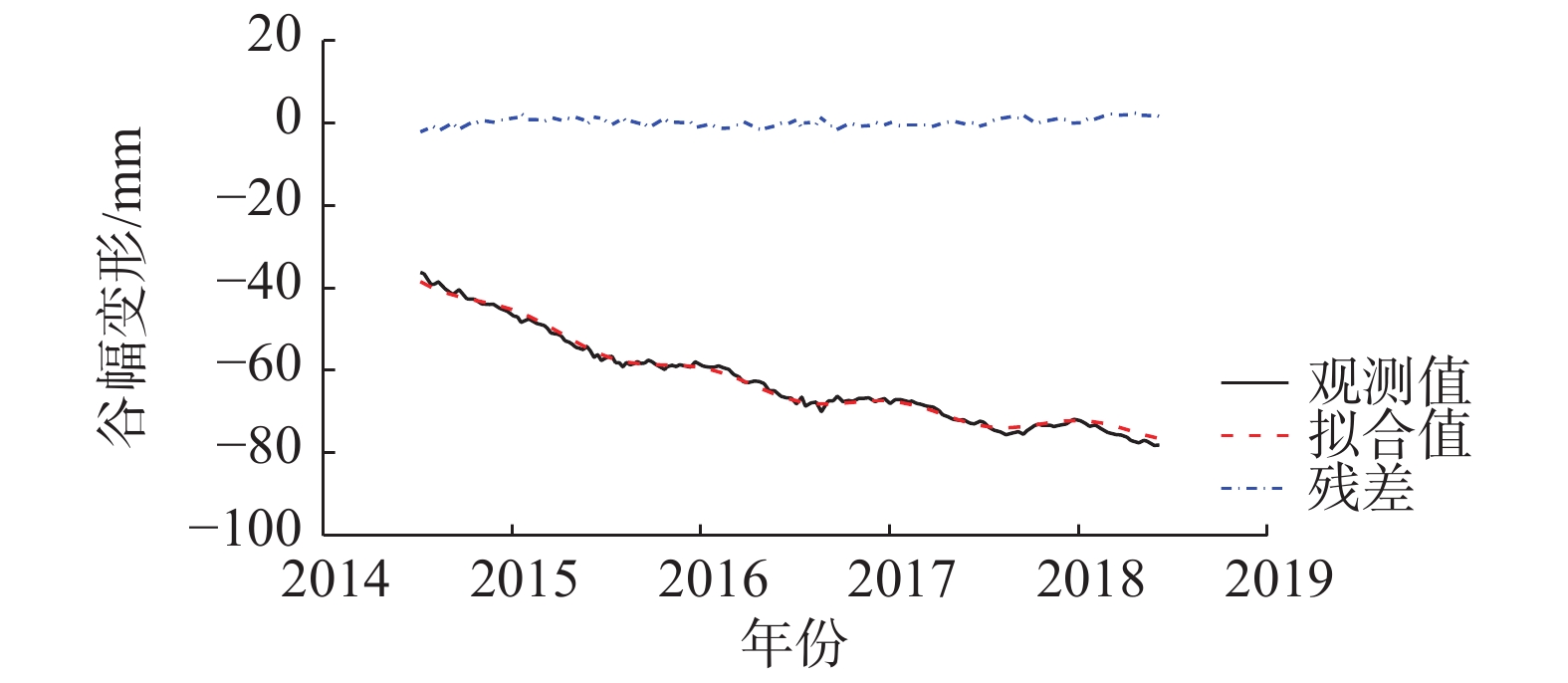
表 1 模型构建考虑的实测温度变量Table 1. Measured temperature variables considered in model construction垂线段 PL15-5 PL15-4 PL15-3 PL15-2 PL15-1 选取的温度计 T6,S3-1,S6-4,S6-9 T14,T15 S5-4,T18 S5-5,T28 T29 自蓄水以来,在坝址上下游侧均观测到了显著的、持续收缩的谷幅变形。如图2,坝肩VDL04测线获得的谷幅变形呈指数函数变化,且存在小的周期性波动。因此,由式(2)和(3)组合表示的时效变量拟合谷幅变形,采用非线性最小二乘法得γ=0.15,R2=0.993,拟合效果如图5。可见,时效变量δθ、δr
还可以较好地表达谷幅变形。最终考虑的变量包括库水位、选取的实测温度(表1)、时效变量δθ和δr。 3.3 模型构建
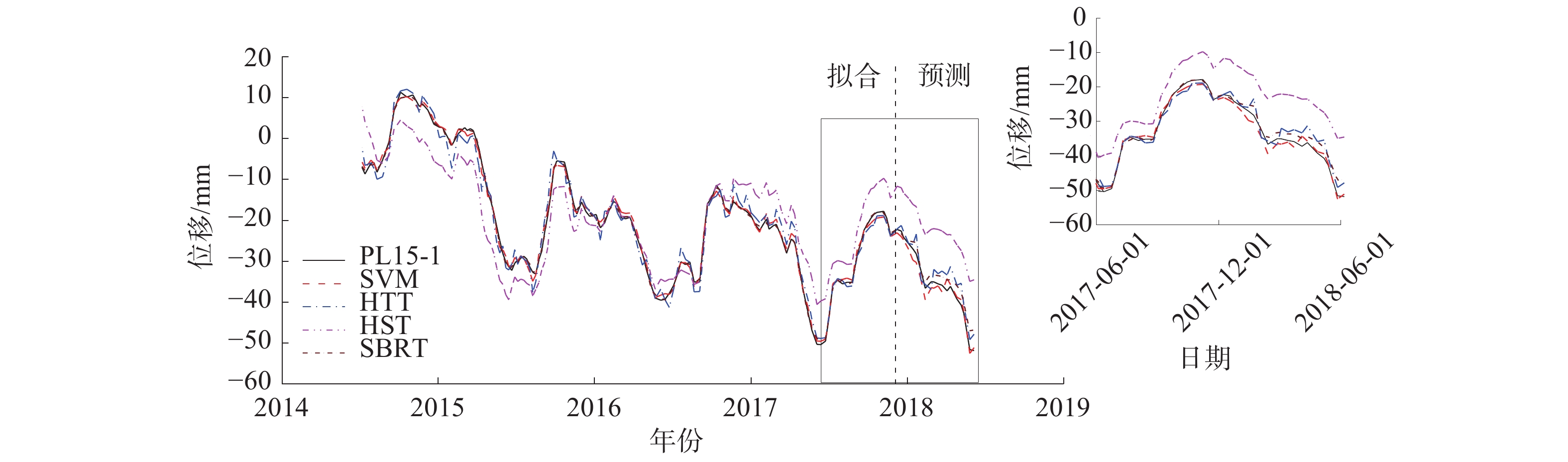
一般地,选取样本总数的10%~20%作为预测集[13],考虑到运行初期的非线性,选取15%作为预测集。SBRT模型构建时的参数按3.2节方法选取。十重交叉验证得到的最优的树的数量为7 050。为对比分析,还构建了SVM,HTT,HST等3种模型,其中,SVM的因子与BRT完全一致。SVM也采用了十重交叉验证优化参数,选择最佳的惩罚因子、不敏感系数取值范围分别为[10, 1 000],[0.000 1, 1],最优值分别为1 000和0.001。HTT和HST采用最小二乘法拟合。HTT模型的实测温度因子与SBRT模型相同。各模型的训练和预测的精度列于表2,SBRT模型最终选取的变量为H,δθ
,δr,S6-9,S6-4和Ta等(其中Ta为空气温度)。各模型的训练和预测效果如图6。 表 2 各模型的训练集和预测集的平均绝对误差Table 2. Comparisons of mean absolute errors among training and prediction sets of constructed models单位:mm 模型 SBRT SVM HTT HST 训练 预测 训练 预测 训练 预测 训练 预测 平均绝对误差 0.42 0.84 0.95 1.49 1.83 3.07 5.96 6.62 3.4 部分依赖图
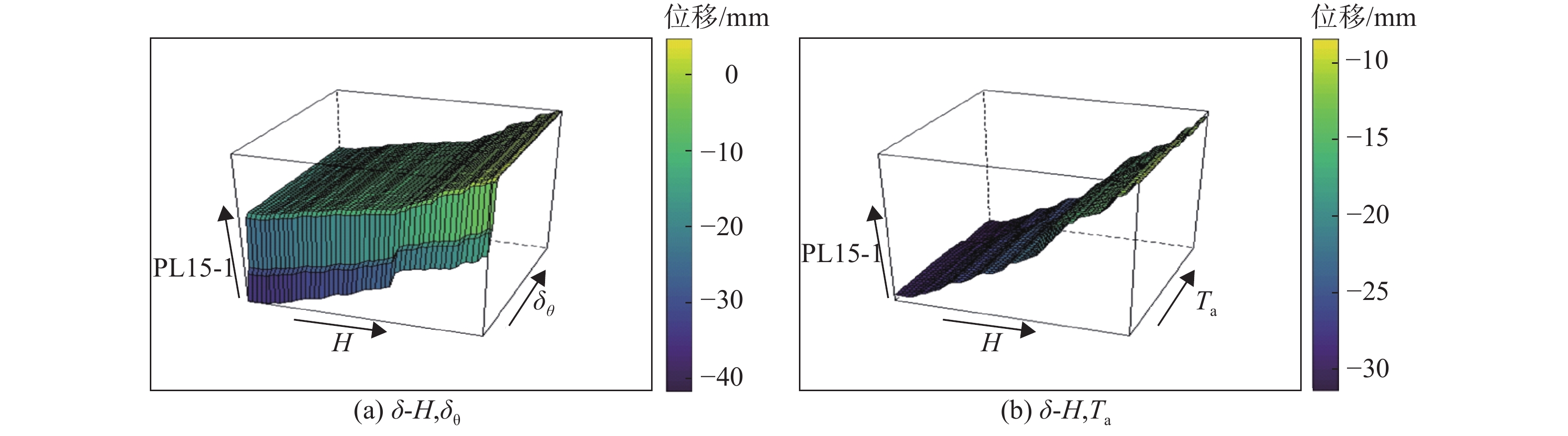
PDP基于模型学习得到每个变量对效应量的边际效应,为此,可通过PDP识别变量-效应量间的关系。PDP可以排除其他变量,仅直观显示一个或一组变量与效应量响应间的关系。因篇幅限制,仅列出了H和δθ,H和Ta与PL15-1的三维PDP关系,如图7。
4. 结果讨论
4.1 变量选取
从图3、表1可看出,388.7 m高程以下库水温基本稳定,温度变幅较小,选取了T6,S3-1,S6-4,S6-9等下游和内部共4个测点;400~480 m高程库水温存在年变化,年变幅小于气温,且与气温存在较大的相位差,内部温度主要受环境温度影响,选取了T14和T15等2个环境温度测点;500~540 m高程库水温存在明显的年变化,但坝体内部水化热温升明显,选取了S5-4,T18,S5-5,T28等下游和内部共4个测点;540 m高程库水温受上游来水温度和气温双重影响,但主要受气温影响,选取了上游测点T29。可见,上游面在温跃层、表温层均选取了典型测点(T15和T29)。各区坝体温度从封拱后都存在温升现象,内部测点主要受水化热控制,以单调温升为主。底高程温度渐趋稳定,高高程受水化热影响仍持续温升,选取的S5-4和S5-5测点(图3)尤为典型。BRT初步选定的变量为19个,SBRT削减了影响较小的变量,仅选取H,δθ,δr,S6-9,S6-4和Ta
等6个变量。 4.2 模型对比分析
由表2可看出,SBRT模型的训练集和测试集精度最高,其次为SVM模型。HTT和HST模型的精度相对较差,HST模型最差。
从SBRT模型及其IR分析结果可知,最主要的影响因素是δθ,H和δr,其值分别为47.15%,27.88%和9.80%。可见,坝体和坝基的徐变及其恢复项对运行初期的变形影响较大,水压荷载次之。对比HTT和HST模型,分析HTT模型能否在一定程度上反映坝体的非稳定温度场,从而改善HST模型的缺陷。
通过非参数方法和多元线性模型对比可知,受非线性时效和非稳定温度场影响,坝体变形表现出显著的非线性,HST和HTT等多元线性模型不适应,其精度不足以准确预测预报。SBRT和SVM均具备较高的精度,但SVM不能较好地联系和分析坝体变形机制,SBRT根据IR判断变量对效应量的影响大小,并使用PDP通过边际效应识别变量对效应量的影响规律。
4.3 变形机制分析
由图7可知,库水位上升时,坝顶变形与库水位之间近似呈线性关系,且变形与库水位变化之间具有同步性、连续性的特征。库水位的多次式影响不显著。
由于坝体、坝基徐变的影响,运行初期坝体整体表现出向上游的变形趋势,2015年6月后变形速率有所减小,但未收敛。加载卸荷引起的弹性位移也有相对较强的影响。考虑到时效能很好地表示谷幅变形,可将坝体总体出现相对向上游变形的特征归结于谷幅变形。此外,坝体内部温度的缓慢回升也使得坝体产生了轻微的向上游变形[14-15]。可见,蓄水初期特高拱坝的变形是一个复杂的非线性过程,其影响因素主要包括时效、库水位、温度回升引起的回弹变形等。
5. 结 语
本文提出了特高拱坝运行初期变形监测和预报模型,得到以下主要结论:
(1)通过HCPC方法选取典型温度测点,以其温度测值作为温度变量,减少了实测温度变量的冗余,温度变量选取结果也反映了环境和坝体内部温度非稳定特征。
(2)引入包含徐变及其恢复项的运行初期时效变量,并对谷幅变形进行了拟合,结果表明时效变量能较好地表征谷幅变形。
(3)提出了基于SBRT方法的运行初期变形监测和预报模型。工程应用表明,SBRT模型具有高拟合和预测精度,并能解释各变量的影响大小;SVM模型次之;HTT和HST模型精度差,不适用于运行初期变形预测。借助变量相对影响和部分依赖图,SBRT模型可直观体现主要变量对变形的影响,有利于特高拱坝运行初期的安全监控和管理。可见,基于SBRT的特高拱坝运行初期变形监测和预警模型具有显著优越性。
-
表 1 模型构建考虑的实测温度变量
Table 1 Measured temperature variables considered in model construction
垂线段 PL15-5 PL15-4 PL15-3 PL15-2 PL15-1 选取的温度计 T6,S3-1,S6-4,S6-9 T14,T15 S5-4,T18 S5-5,T28 T29 表 2 各模型的训练集和预测集的平均绝对误差
Table 2 Comparisons of mean absolute errors among training and prediction sets of constructed models
单位:mm 模型 SBRT SVM HTT HST 训练 预测 训练 预测 训练 预测 训练 预测 平均绝对误差 0.42 0.84 0.95 1.49 1.83 3.07 5.96 6.62 -
[1] 张冲, 王仁坤, 汤雪娟. 溪洛渡特高拱坝蓄水初期工作状态评价[J]. 水利学报,2016,47(1):85-93. (ZHANG Chong, WANG Renkun, TANG Xuejuan. Safety evaluation of Xiluodu ultra-high arch dam during the initial impoundment period[J]. Journal of Hydraulic Engineering, 2016, 47(1): 85-93. (in Chinese) [2] 何柱, 刘耀儒, 杨强, 等. 溪洛渡拱坝谷幅变形机制及变形反演和长期稳定性分析[J]. 岩石力学与工程学报,2018,37(增刊2):4198-4206. (HE Zhu, LIU Yaoru, YANG Qiang, et al. Mechanism of valley deformation of Xiluodu arch dam and back analysis and long-term stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(Suppl2): 4198-4206. (in Chinese) [3] 刘宁. 国内外大坝失事分析研究[M]. 武汉: 湖北科学技术出版社, 2002. LIU Ning. Analysis and research of dam-failure[M]. Wuhan: Hubei Science and Technology Press, 2002. (in Chinese)
[4] 顾冲时, 苏怀智, 王少伟. 高混凝土坝长期变形特性计算模型及监控方法研究进展[J]. 水力发电学报,2016,35(5):1-14. (GU Chongshi, SU Huaizhi, WANG Shaowei. Advances in calculation models and monitoring methods for long-term deformation behavior of concrete dams[J]. Journal of Hydroelectric Engineering, 2016, 35(5): 1-14. (in Chinese) doi: 10.11660/slfdxb.20160501 [5] 顾冲时, 吴中如. 大坝与坝基安全监控理论和方法及其应用[M]. 南京: 河海大学出版社, 2006. GU Chongshi, WU Zhongru. Theory and method of dam and dam foundation safety monitoring and their applications[M]. Nanjing: Hohai University Press, 2006. (in Chinese)
[6] HU J, WU S H. Statistical modeling for deformation analysis of concrete arch dams with influential horizontal cracks[J]. Structural Health Monitoring, 2019, 18(2): 546-562. doi: 10.1177/1475921718760309
[7] SALAZAR F, MORÁN R, TOLEDO M Á, et al. Data-based models for the prediction of dam behaviour: A review and some methodological considerations[J]. Archives of Computational Methods in Engineering, 2017, 24(1): 1-21. doi: 10.1007/s11831-015-9157-9
[8] KANG F, LI J J, DAI J H. Prediction of long-term temperature effect in structural health monitoring of concrete dams using support vector machines with Jaya optimizer and salp swarm algorithms[J]. Advances in Engineering Software, 2019, 131: 60-76. doi: 10.1016/j.advengsoft.2019.03.003
[9] SALAZAR F, TOLEDO M Á, GONZÁLEZ J M, et al. Early detection of anomalies in dam performance: A methodology based on boosted regression trees[J]. Structural Control and Health Monitoring, 2017, 24(11): e2012. doi: 10.1002/stc.2012
[10] 彭卫, 杜时贵. 混凝土徐变效应的计算机分析[J]. 西安公路交通大学学报,1999,19(2):4-5, 9. (PENG Wei, DU Shigui. Computational analysis of concrete creep effect[J]. Journal of Xi'an Highway University, 1999, 19(2): 4-5, 9. (in Chinese) [11] ABDI H, WILLIAMS L J. Principal component analysis[J]. WIREs Computational Statistics, 2010, 2(4): 433-459. doi: 10.1002/wics.101
[12] LI Q B, ZUO Z, HU Y, et al. Smart monitoring of a super high arch dam during the first reservoir-filling phase[J]. Journal of Aerospace Engineering, 2017, 30(2): B4016001.
[13] SALAZAR F, TOLEDO M A, OÑATE E, et al. An empirical comparison of machine learning techniques for dam behaviour modelling[J]. Structural Safety, 2015, 56: 9-17. doi: 10.1016/j.strusafe.2015.05.001
[14] 张国新, 周秋景. 特高拱坝封拱后温度回升及影响研究[J]. 水利学报,2015,46(9):1009-1018. (ZHANG Guoxin, ZHOU Qiujing. Study on temperature recovery after arch sealing of super high arch dams and its influence[J]. Journal of Hydraulic Engineering, 2015, 46(9): 1009-1018. (in Chinese) [15] 高俊, 黄耀英, 万智勇, 等. 含冷却水管混凝土坝温度计埋设位置优选[J]. 水利水运工程学报,2017(3):93-98. (GAO Jun, HUANG Yaoying, WAN Zhiyong, et al. Optimization analysis of setting location of thermometer in concrete dam with cooling water pipes[J]. Hydro-Science and Engineering, 2017(3): 93-98. (in Chinese) -
期刊类型引用(12)
1. 俞扬峰,娄本星,马福恒,叶伟,李星,罗翔. 基于空间面板数据模型的拱坝变形缺失数据处理. 水利水运工程学报. 2024(02): 135-142 .  本站查看
本站查看
2. 胡江,苏荟. 水工结构变形预测模型构建与解释. 水利水运工程学报. 2024(02): 125-134 .  本站查看
本站查看
3. 朱宝强,陈宇龙,韩继宗,彭浩. 某300 m级特高拱坝运行初期渗流特性分析. 水电与新能源. 2024(10): 55-59 .  百度学术
百度学术
4. 周心怡,胡蕾,张启灵. 考虑谷幅收缩变形的高拱坝多源信息融合安全评判. 长江科学院院报. 2023(01): 87-93 .  百度学术
百度学术
5. 魏攀哲,赵引. 岩体劣化对谷幅变形及高拱坝安全性的影响. 水利水运工程学报. 2023(02): 104-112 .  本站查看
本站查看
6. 葛盼猛,陈波,陈伟楠,朱明远. 基于OWOA-RFWSVR-DLM的高寒区混凝土坝变形预测模型. 长江科学院院报. 2023(05): 153-159+165 .  百度学术
百度学术
7. 胡江,王春红,李星. 改进的特高拱坝分区变形预测模型. 水力发电学报. 2023(07): 69-83 .  百度学术
百度学术
8. 王文娟,纪丁愈,李云祯. 特高拱坝施工期谷幅变形演化规律. 水利水运工程学报. 2022(03): 82-89 .  本站查看
本站查看
9. 胡江,张吉康,余梦雪,马福恒,肖文素. 深挖方膨胀土渠道边坡变形特征分析与预测. 水利水运工程学报. 2021(04): 1-9 .  本站查看
本站查看
10. 辛长虹,赵引. 考虑非饱和渗流的谷幅变形对高拱坝影响分析. 水利水运工程学报. 2021(04): 36-45 .  本站查看
本站查看
11. 周仁练,苏怀智,韩彰,徐朗,刘明凯. 混凝土坝变形的长期预测模型与应用. 水力发电学报. 2021(09): 122-131 .  百度学术
百度学术
12. 黄永涛,刘晓青,季威,王雪红. HCM-PSO-GRU组合预测模型在大坝变形预测中的应用. 水电能源科学. 2021(12): 120-123+61 .  百度学术
百度学术
其他类型引用(4)



 Email Alerts
Email Alerts RSS
RSS
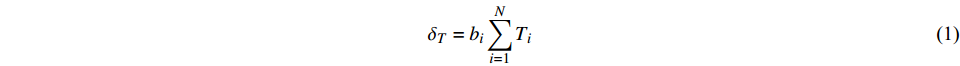
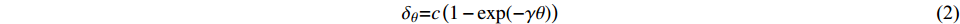
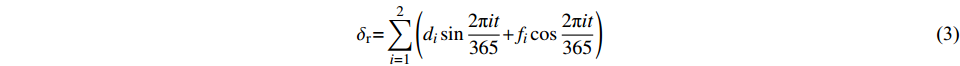
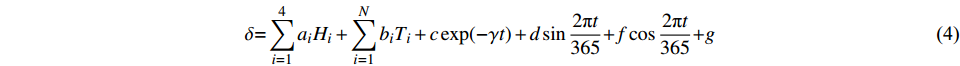
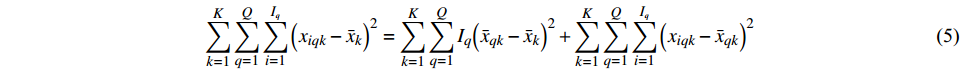
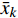

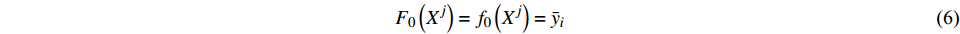
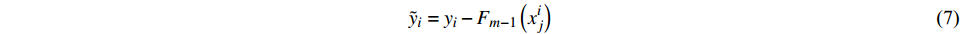
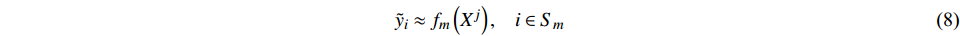
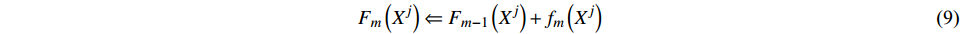
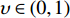
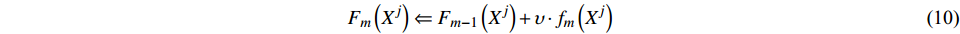
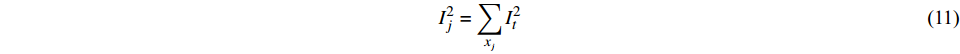
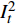
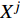
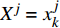
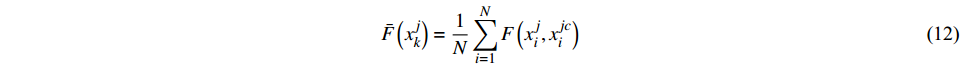
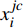
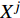
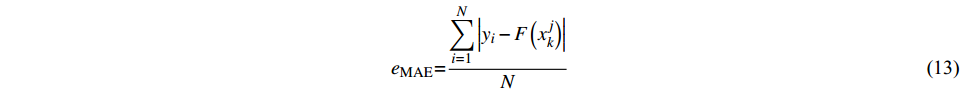
 下载:
下载: