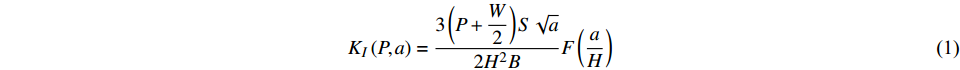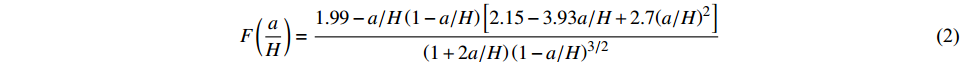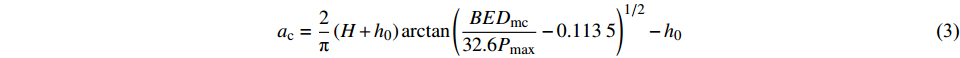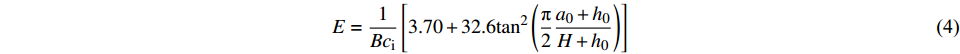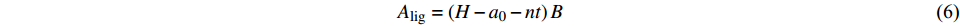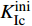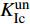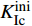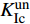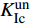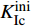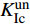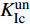Email Alerts
RSS
Effect of internal crack defects on fracture properties of concrete
-
摘要: 为研究混凝土梁内部贯穿裂缝缺陷对其断裂性能的影响，设计了含不同裂缝缺陷混凝土梁的三点弯曲断裂试验，研究不同长度、位置及数量的水平裂缝缺陷对混凝土断裂性能的影响。通过试验测得的P-Dm曲线以及相关试验数据计算得到含不同裂缝缺陷的混凝土断裂参数与断裂能。对比结果可知：混凝土三点弯曲梁的起裂荷载和起裂韧度受水平裂缝缺陷参数变化的影响较小，而失稳荷载和失稳韧度受水平裂缝缺陷的影响较大；水平裂缝越长，试验测得其失稳荷载越小，计算得到的失稳韧度和断裂能也越小。水平裂缝距离试件的底部越近，试验测得其失稳荷载越小，计算得到的失稳韧度和断裂能也越小。水平裂缝数量越多，试验测得其失稳荷载越小，计算得到的失稳韧度越小，断裂能也越小。该现象表明混凝土试件中含线性缺陷导致材料的缺失量越大，其完全断裂所消耗的能量越小，且测得的断裂参数值也越小。Abstract: Concrete beams with different types of horizontal crack defect were designed and tested through the three-point bending test to investigate the influence of internal crack defect on the fracture behavior of concrete. The effects of different lengths, locations, and numbers of horizontal crack defects on the fracture performance of concrete were analyzed. The fracture parameters and fracture energy of the concrete within different crack defects were calculated and compared on the basis of P-Dm and related test data. Results show that the initial cracking load and initiation fracture toughness of the concrete beams were slightly affected by the internal horizontal crack defects, whereas unstable load and fracture toughness were seriously affected by the additional horizontal crack defects. A large horizontal crack length and a small distance between the horizontal crack and the bottom of the beam corresponded to a small carrying capacity of the beam and a small unstable fracture toughness and fracture energy. The more the horizontal cracks in the concrete beams were, the smaller the unstable load and the unstable fracture toughness were and the smaller the fracture energy was. This phenomenon shows that the larger the material loss caused by crack defects in the concrete beams, the smaller the energy consumed by complete fracture and the smaller the fracture parameters measured.
-
混凝土是现代土木工程中主要的建筑用材，因其自身特性及其各种因素引起的缺陷，对混凝土结构的安全性能有着重要影响[1-2]。裂缝作为混凝土结构内部最常见的缺陷会影响结构的力学承载性能。因此，研究混凝土材料中裂缝缺陷对断裂特性的影响具有重要意义。
断裂力学应用于分析混凝土材料断裂过程以来，带裂缝的混凝土试件包括中央带缺口的三点弯曲梁[3-4]、带初始裂缝的楔入劈拉试件[5-7]以及紧凑拉伸试件[8]随即成为主要的混凝土材料断裂力学性能测试试件。20世纪80年代，徐世烺与Reinhardt等提出了双K断裂模型[9-11]，模型通过引入混凝土材料的起裂和失稳韧度描述裂缝在混凝土材料中断裂的全过程，并提出测试水工混凝土断裂韧度的一般方法[12]。该测试方法被广泛用于工程中混凝土材料断裂力学行为的测试。
近年来，一些学者对缺陷影响材料断裂力学行为进行了研究。胡少伟等[13]利用内部预制孔洞缺陷的楔入劈拉试件分析了混凝土断裂力学测试试验中试件内部缺陷对其断裂力学测试结果的影响，认为当裂缝经过缺陷时会降低相关参数，当其远离缺陷区域时，则影响较小。胡少伟等[14]对含多条预置裂缝的混凝土三点弯曲试验梁的断裂过程进行了测试，试验结果得到次缝对试件测试中的结果具有重大影响。孙国有等[15]将细观空洞的扩张与I-II复合型裂缝相结合并推导出其相应的断裂参数。
本文基于混凝土梁的三点弯曲断裂试验，在试件内部构建不同参数的贯穿裂缝缺陷，通过试验获得的断裂特征曲线结合双K断裂模型计算获得其断裂参数与断裂能，并对计算结果进行对比分析，从而得到混凝土试件内部含裂缝缺陷及缺陷参数对断裂测试结果的影响。
1. 试验概况
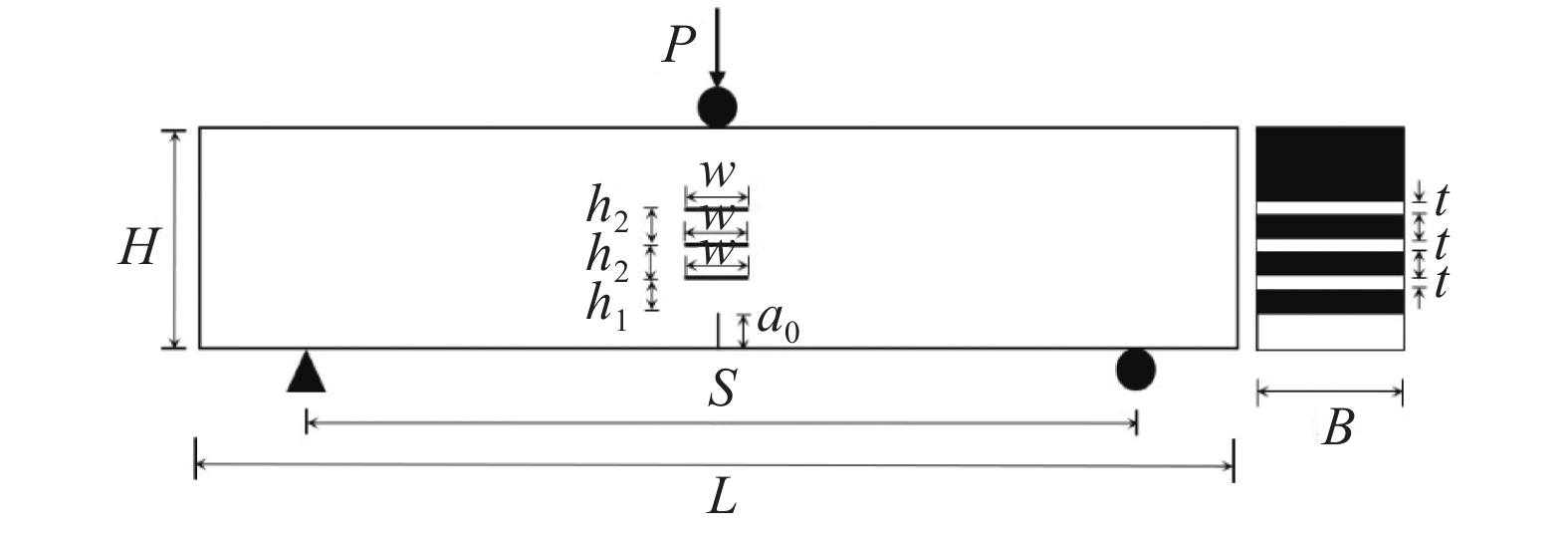
试验设计了10组共30个标准三点弯曲梁试件(S/H=4)，试件尺寸均为L×H×B=1 000 mm×200 mm×120 mm，其中含有n个水平裂缝缺陷，试件形式如图1所示。图中h1为边缘裂缝尖端至第1个内部裂缝缺陷中心的距离，h2为两相邻内部裂缝缺陷的距离，其中内部裂缝缺陷中心均在边缘裂缝延长线上，w为内部裂缝缺陷的长度，a0为边缘缝高度（本试验中设为40 mm），混凝土三点弯曲梁试件的裂缝设计参数见表1。
表 1 试件设计参数Table 1. Design parameters of specimens试件编号 w/mm n h1/mm h2/mm TPB-W1-x 60 1 40 - TPB-W2-x 80 1 40 - TPB-W3-x 100 1 40 - TPB-W4-x 120 1 40 - TPB-H1-x 60 1 20 - TPB-H2-x 60 1 40 - TPB-H3-x 60 1 60 - TPB-H4-x 60 1 80 - TPB-N1-x 60 0 - - TPB-N2-x 60 1 40 - TPB-N3-x 60 2 40 20 TPB-N4-x 60 3 20 20 注：试件编号中，TPB代表三点弯曲梁试验；W，H，N分别代表含不同长度w、间距h1和h2以及数量n的水平裂缝缺陷的试件；x = 1，2，3，代表相同参数的试件各有3个。 试件采用的混凝土由42.5普通硅酸盐水泥、最大粒径为20 mm的石灰岩碎石和天然河砂配制而成，配合比为水泥∶砂∶石∶水=1∶1.225∶2.485∶ 0.440。混凝土混合料在振动下浇注到木模中，试件边缘预制缝以及内部裂缝缺陷分别采用厚3 mm、一端为30°V型和两端均为30°V型的不锈钢板预埋，钢板在初凝后终凝前拔出。混凝土标准立方体试件28 d龄期抗压强度、抗拉强度、杨氏模量和泊松比分别为：fc=46.7 MPa，ft=3.46 MPa，e=33.0 GPa和μ=0.2。
混凝土三点弯曲梁试件的断裂测试试验在20 t电子伺服万能压力机上进行，试验现场装置如图2所示，试验中压力机的垂直加载速率小于10 N/s，试验加载前进行预加载以确保仪器及测试传感装置的准确连接。试验中所有试验数据采用DH5902动态数据采集仪采集，采集的试验数据包括：由压力传感器获取的外加垂直荷载、由竖向位移计获取的试件中心竖向位移、由夹式引伸计获取的竖缝口张口位移、由应变片获取的竖缝裂尖应变和横缝上端应变（图3）。
试件的破坏形态和断裂路径如图4所示。可见水平裂缝缺陷在裂缝扩展路径上，且裂缝穿过水平裂缝缺陷后仍保持I型的断裂模式扩展路径。
2. 混凝土三点弯曲梁断裂性能参数计算方法
2.1 断裂参数计算方法
根据文献[9-11]，并结合《水工混凝土断裂试验规程》（DL/T 5332—2005）计算三点弯曲梁试件的断裂韧度。
$$ {K_I}\left( {P,a} \right) = \dfrac{{3\left( {P + \dfrac{W}{2}} \right)S\sqrt a }}{{2{H^2}B}}F\left( {\dfrac{a}{H}} \right) $$ (1) $$F\left( {\frac{a}{H}} \right) = \frac{{1.99 - a/H\left( {1 - a/H} \right)\left[ {2.15 - 3.93a/H + 2.7{{\left( {a/H} \right)}^2}} \right]}}{{\left( {1 + 2a/H} \right){{\left( {1 - a/H} \right)}^{3/2}}}}$$ (2) 式中：P为外加荷载值；W为试件支座间梁的自重，由试件总重量乘以S
/ L计算得到；S为试件两支座间的跨度；a为裂缝长度；H，B和L分别为试件的高度、厚度和长度。 根据双K断裂准则[11]，计算混凝土起裂韧度Kini时，仅需将起裂荷载Pini和边缘预制缝长度a0代入上述公式即可；计算混凝土失稳韧度Kun时，将失稳荷载Pun和临界有效裂缝长度ac代入上述公式即可。其中，ac按下式计算：
$${a_{\rm{c}}} = \frac{2}{{\text{π}}}\left( {H + {h_0}} \right)\arctan {\left( {\frac{{BE{D_{{\rm{mc}}}}}}{{32.6{P_{\max }}}} - 0.113\;5} \right)^{1/2}} - {h_0}$$ (3) 式中：h0为钢片刀口厚度；E为计算弹性模量；Dmc为临界裂缝张口位移，即试件P-Dm曲线中峰值荷载Pmax所对应的值。其中，E按下式计算：
$$E = \frac{1}{{B{c_{\rm{i}}}}}\left[ {3.70 + 32.6{{\tan }^2}\left( {\frac{{\text{π}}}{2}\frac{{{a_0} + {h_0}}}{{H + {h_0}}}} \right)} \right]$$ (4) 式中：ci为试件初始Dm/P值，由P- Dm曲线上升直线段上任一点的Dm和P计算可得。
2.2 断裂能计算方法
根据三点弯曲梁试验测得的荷载-位移全过程曲线，采用RILEM(国际材料和结构试验室联合会)推荐的公式[16]计算混凝土的断裂能。
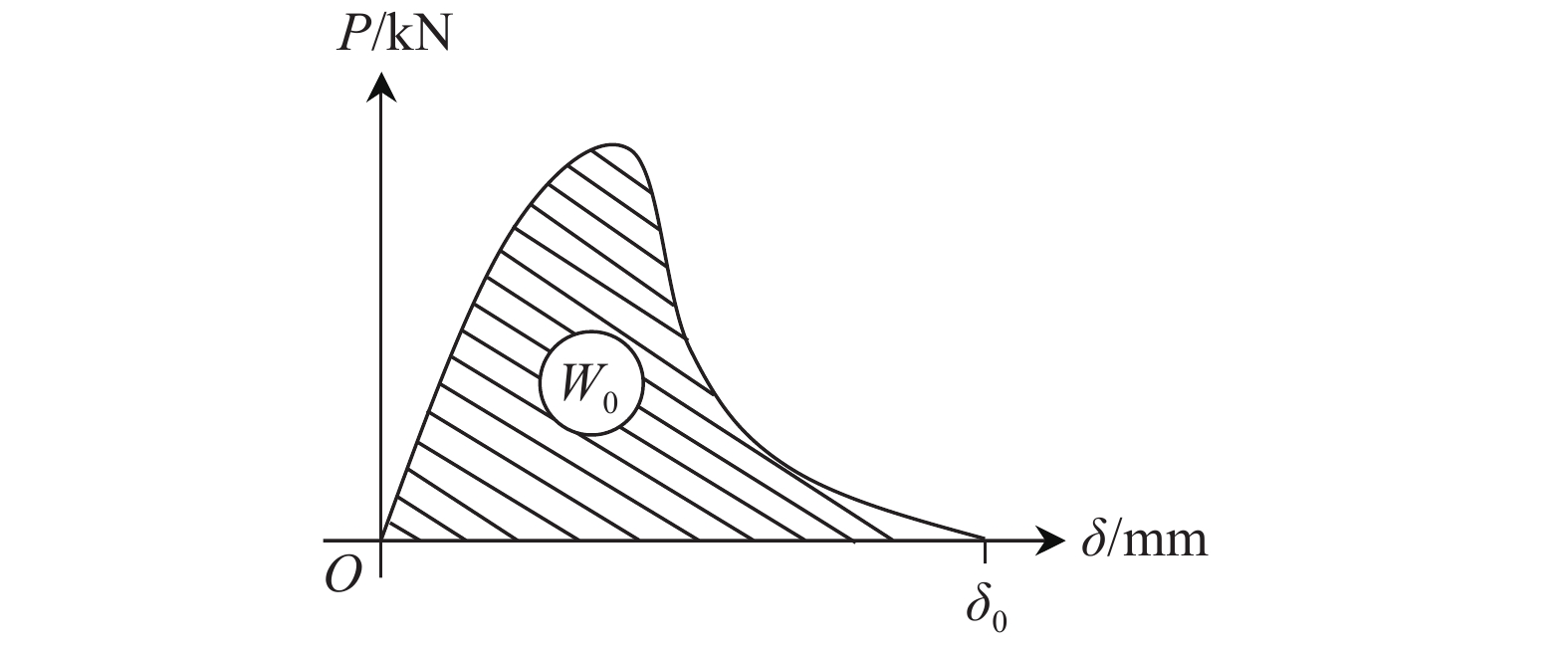
$${G_{\rm{f}}} = \left( {{W_0} + mg{\delta _0}} \right)/{A_{{\rm{lig}}}}$$ (5) 式中：W0为荷载-位移（P-δ）曲线下所围图形的面积（图5）；δ0为梁完全断裂时的加载点位移；m为支座间梁的质量；g为重力加速度，取为9.81 m/s2；Alig为混凝土梁断裂带在垂直于梁轴平面上的投影面积。Alig按下式计算：
$${A_{{\rm{lig}}}} = \left( {H - {a_0} - nt} \right)B$$ (6) 式中：H和B分别为梁的高度和厚度；a0为边缘缝高度；n为水平裂缝缺陷数量；t为水平缺陷厚度。
3. 水平裂缝缺陷对混凝土断裂性能的影响
3.1 水平裂缝缺陷长度对混凝土断裂性能的影响
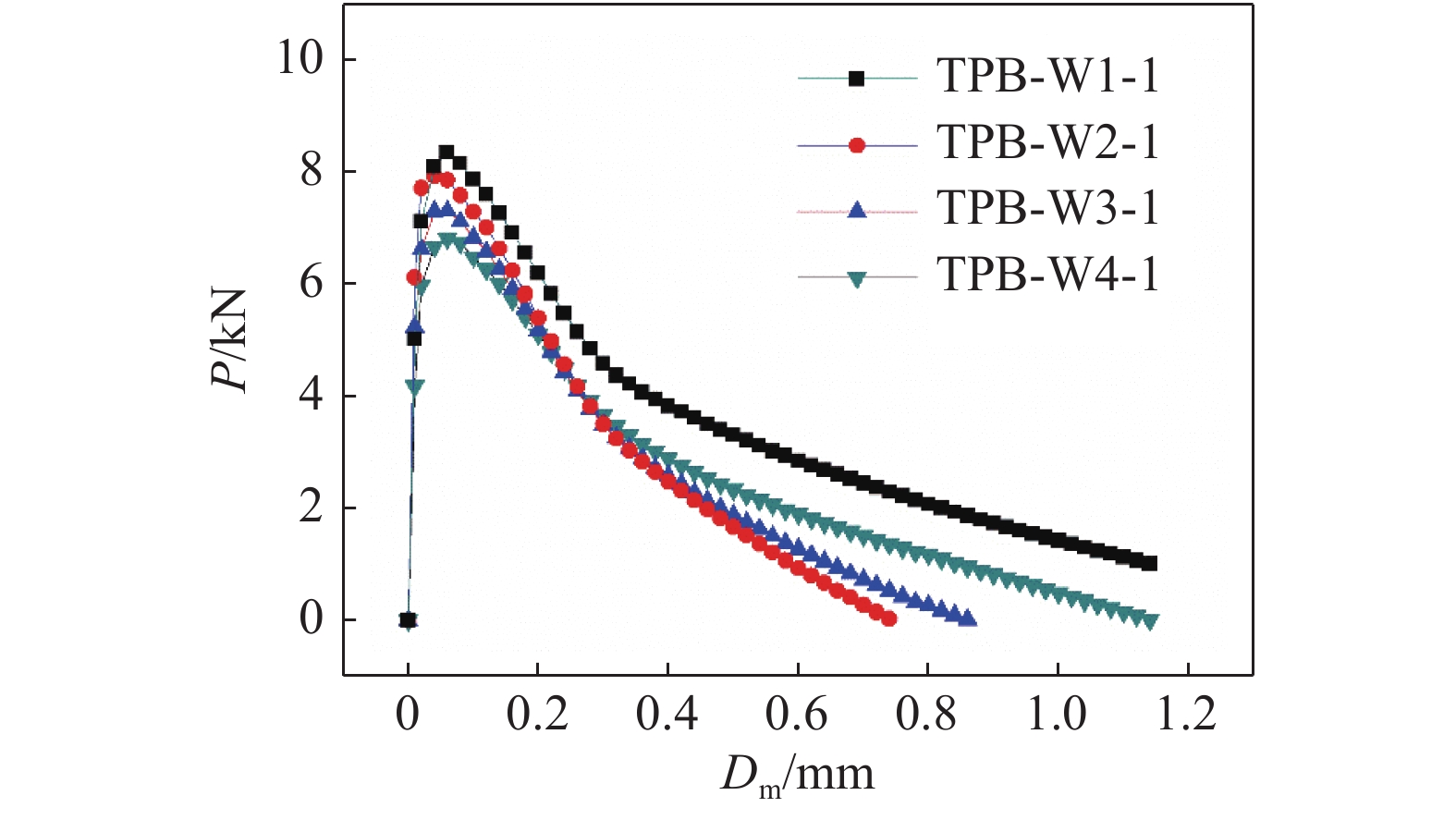
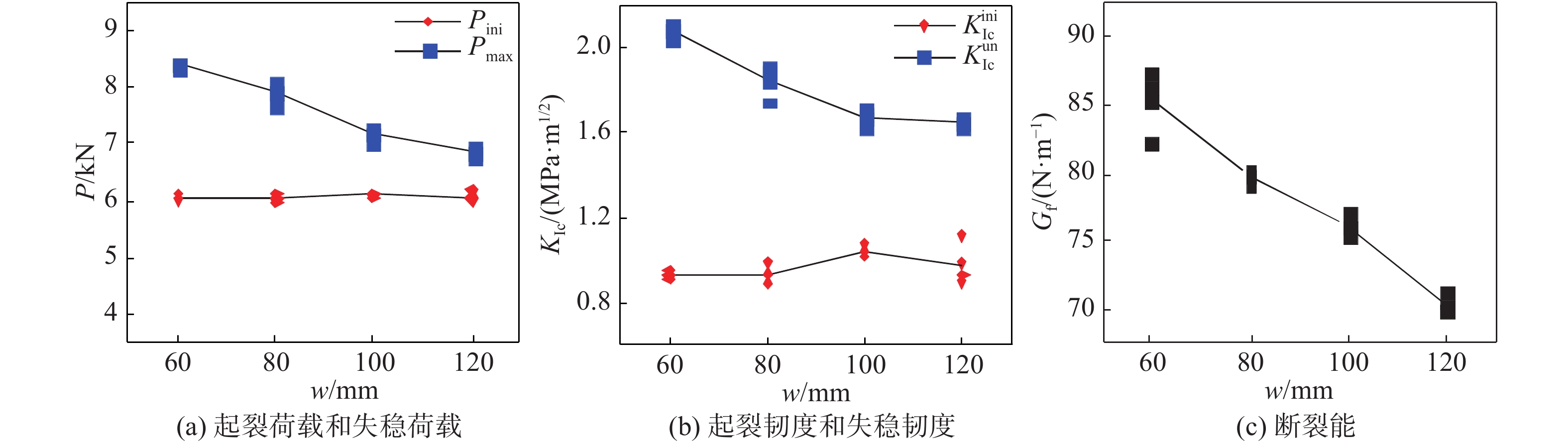
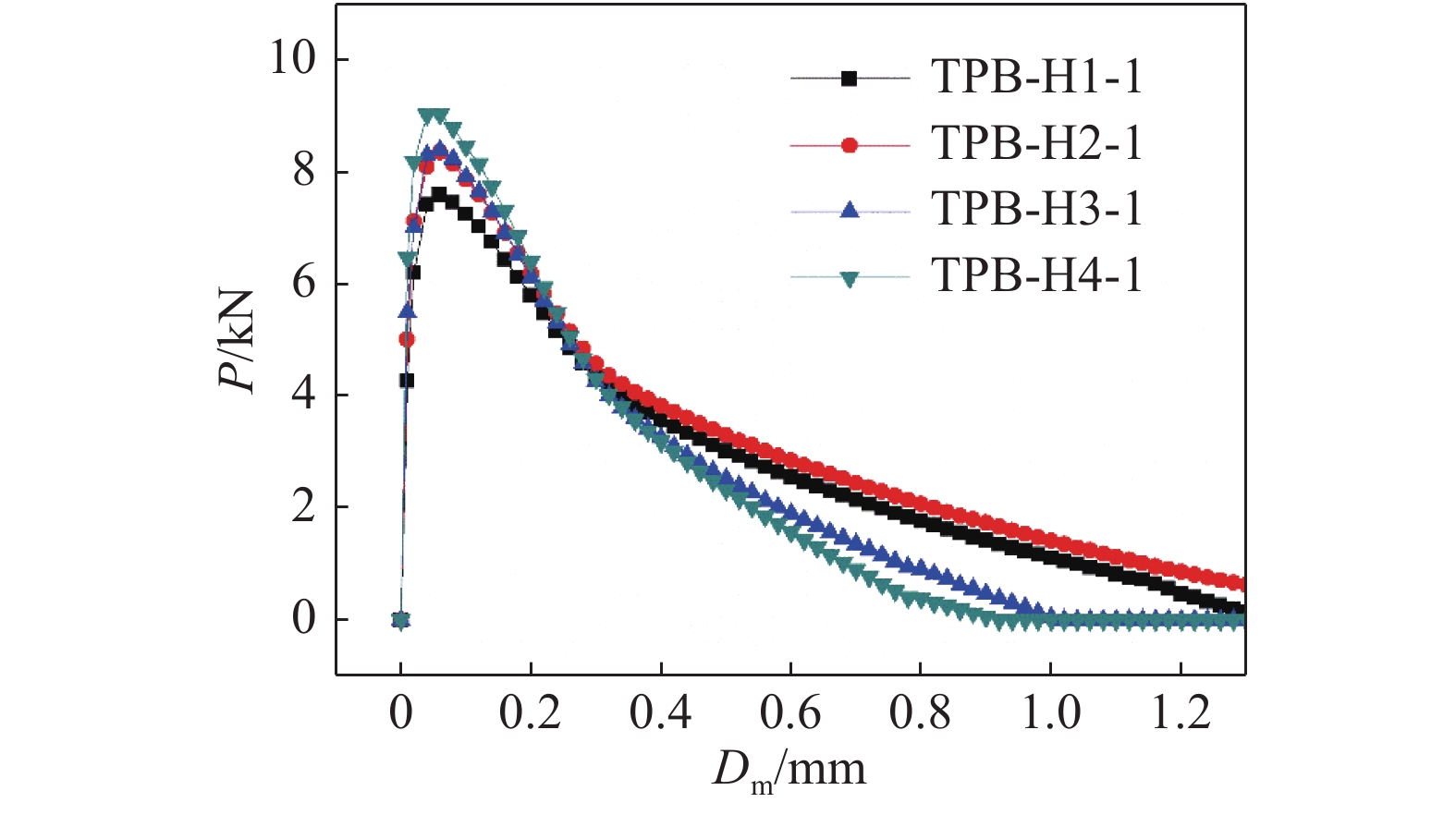
图6给出了混凝土梁内部含不同长度水平裂缝缺陷的P-Dm曲线。可见，各组试件的P-Dm曲线规律相似，并且与无缺陷梁的曲线相似，即试件的断裂过程依然呈现出典型的三阶段式，分别为线弹性阶段、稳定扩展阶段和失稳扩展阶段。第1阶段，混凝土梁中未出现裂纹，荷载与裂缝口张开位移呈线性关系；第2阶段，随着荷载的增大，混凝土梁开始出现微裂纹并且形成断裂过程区，裂缝的张口位移增加速度加快，裂缝稳定扩展，P-Dm曲线呈非线性增长；第3阶段，混凝土梁达到极限承载能力，试件中裂缝迅速扩展最终导致其完全断裂失效，在P-Dm曲线上表现为荷载突然降低同时张口位移迅速增加。由测得的P-Dm曲线，曲线峰值前的线性段至非线性段的拐点对应的荷载为起裂荷载Pini（同时也是预制缝尖端P-ε曲线上应变最大值对应的荷载值），峰值对应的荷载以及裂缝口张开位移分别为失稳荷载Pmax和临界张口位移Dmc，同时根据式(1)~ (6)计算可得起裂韧度、失稳韧度以及断裂能。图7给出了计算所得的断裂参数随水平裂缝长度的变化。随着水平裂缝缺陷长度从60 mm增至120 mm，测试的混凝土梁起裂荷载Pini保持约为6 kN不变，起裂韧度
$K_{{\rm{Ic}}}^{{\rm{ini}}}$ 约为1 MPa·m1/2保持不变，而试件的失稳荷载Pmax从8.39 kN减到6.87 kN，减小了18.1%，失稳韧度$K_{{\rm{Ic}}}^{{\rm{un}}}$ 从2.08 MPa·m1/2降至1.65 MPa·m1/2，降低约20%；断裂能Gf从85.29 N/m降至70.43 N/m，降低了17.4%。计算结果表明，试件内部的水平裂缝缺陷对混凝土三点弯曲梁试件的起裂荷载和起裂韧度影响较小，但会加速试件失稳，并且水平裂缝的长度越长，裂缝扩展过程进入失稳破坏阶段越早。由试验测得的Pini/Pmax从0.72增大到0.88可知，水平裂缝缺陷的存在及其长度的增大使得断裂测试中试件断裂过程中的脆性也进一步增大。3.2 水平裂缝缺陷位置对混凝土断裂性能的影响
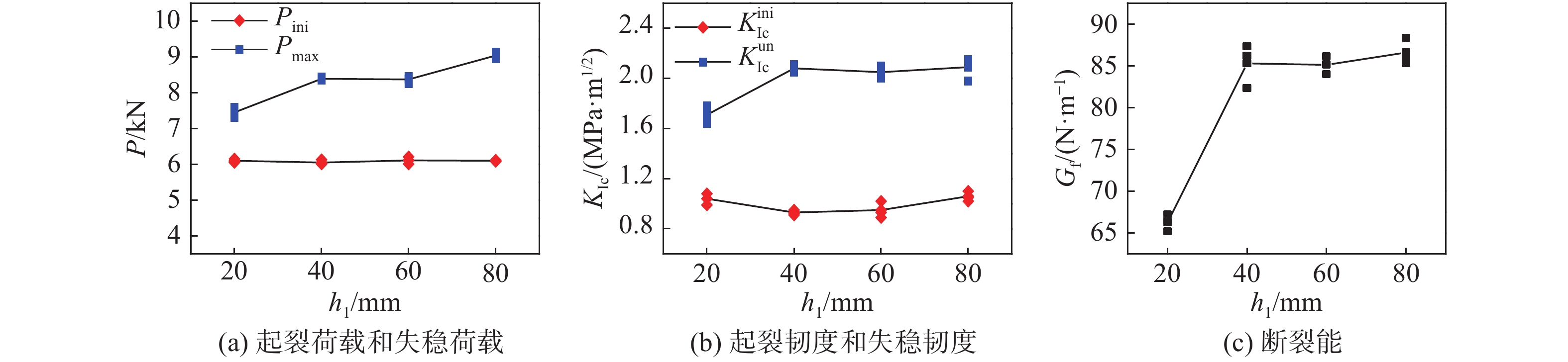
图8给出了含不同位置水平裂缝试件的P-Dm曲线。由图8可知，各组试件的P-Dm曲线呈相似规律，也与无水平裂缝缺陷试样的结果相似，各组试件的断裂过程表征出线弹性、裂缝稳定扩展和裂缝失稳扩展阶段。图9给出了计算所得的断裂参数随水平裂缝位置的变化。由图9可知，由于水平裂缝位置不同，断裂参数有所差异，具体表现为：水平裂缝缺陷位置h1从80 mm降至20 mm，试件的起裂荷载Pini保持在6.05~6.11 kN，计算获得的起裂韧度
$K_{{\rm{Ic}}}^{{\rm{ini}}}$ 保持在0.93~1.06 MPa·m1/2，而测得的失稳荷载Pmax从9.04 kN降至7.45 kN，减少约17.6%，失稳韧度$K_{{\rm{Ic}}}^{{\rm{un}}}$ 从2.09 MPa·m1/2减小到1.71 MPa·m1/2，约减小18.2%，试验测得断裂能Gf从86.59 N/m降至66.26 N/m，减小约23.5%。试验结果表明水平裂缝缺陷与边缘预制缝尖距离h1越小，Pmax和$K_{{\rm{Ic}}}^{{\rm{un}}}$ 越小，试件中裂缝进入失稳扩展阶段越快。又由Pini/Pmax从0.67增大到0.82可知，水平裂缝缺陷的存在及其距离h1的减小，试件的脆性不断增大，测得的断裂参数也越小。3.3 水平裂缝缺陷数量对混凝土断裂性能的影响
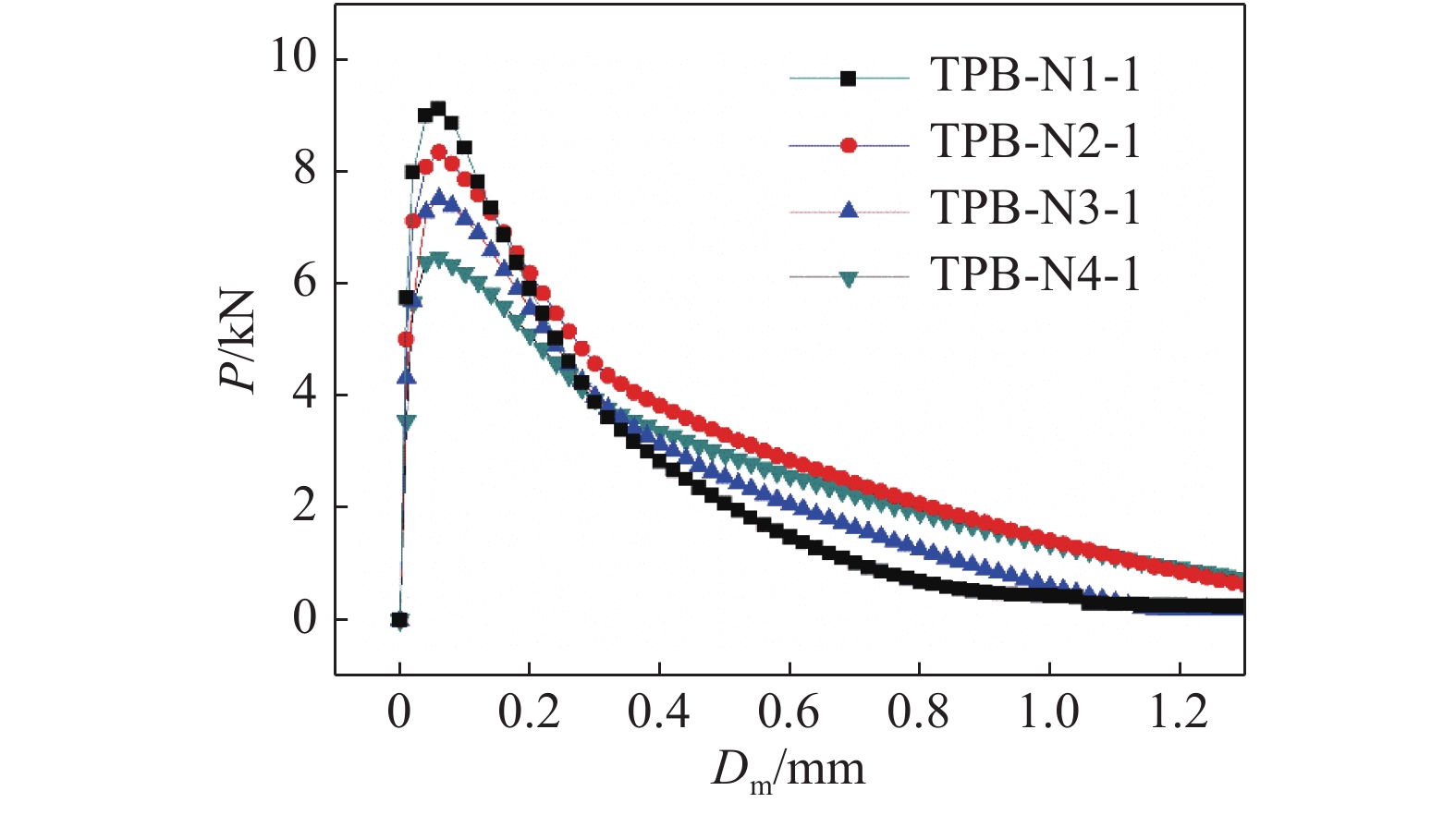
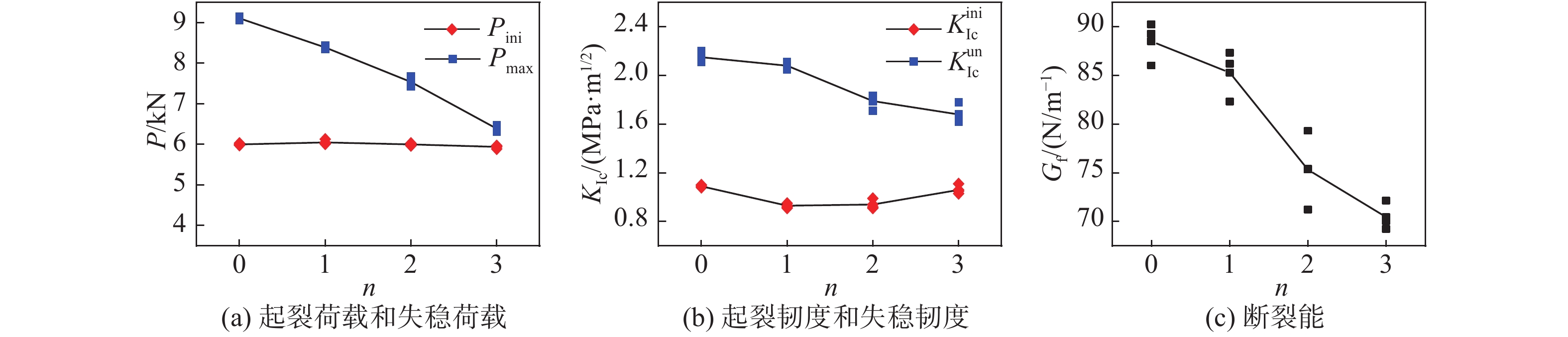
图10给出了含不同水平裂缝缺陷数量的试件的P-Dm曲线。由图可知各组试件的P-Dm曲线呈相似规律，各组试件的断裂过程仍分为3个阶段。图11给出了计算所得的断裂参数随水平裂缝数量的变化。随着水平裂缝缺陷数量由0增加至3，试件的起裂荷载Pini为5.94~6.05 kN，起裂韧度
$K_{{\rm{Ic}}}^{{\rm{ini}}}$ 为0.93~1.09 MPa·m1/2，而试件的失稳荷载Pmax从9.11 kN减到6.39 kN，失稳韧度$K_{{\rm{Ic}}}^{{\rm{un}}}$ 从2.15 MPa·m1/2降至1.68 MPa·m1/2，降低了21.9%，断裂能Gf从88.5 N/m降至70.45 N/m，降低20.4%。试验结果表明，由于水平裂缝缺陷的存在及其数量的增多，Pmax和$K_{{\rm{Ic}}}^{{\rm{un}}}$ 均减小，Pini/Pmax从0.66增大到0.93，试件更早进入失稳断裂过程，混凝土试件的脆性也不断增大。![]()
图 11 断裂参数随水平裂缝数量变化曲线Figure 11. Fracture parameters versus number of horizontal cracks4. 结 语
试验设计了含不同类型水平裂缝缺陷的混凝土梁的三点弯曲断裂试验，主要研究不同长度、位置及数量的水平裂缝缺陷对混凝土断裂性能的影响。依据试验中测得的P-Dm曲线以及相关试验数据计算得到含不同裂缝缺陷混凝土断裂参数与断裂能，对比分析不同参量试件的测试结果，得到以下主要结论：
（1）混凝土内部的水平裂缝缺陷对三点弯曲梁试件的起裂荷载和起裂韧度测试结果影响较小，但是对失稳荷载和失稳韧度的测试结果影响较大。
（2）对含60，80，100和120 mm长度的水平裂缝缺陷的混凝土三点弯曲梁试件进行测试，结果表明断裂韧度和断裂能随裂缝缺陷长度的增加而降低，且裂缝长度由60 mm增至120 mm时，失稳韧度降低约20%，断裂能降低约17.4%。
（3）对距边缘预置缝缝尖20，40，60和80 mm水平裂缝缺陷的混凝土三点弯曲梁试件进行测试，结果表明断裂韧度和断裂能随裂缝缺陷距离的降低而降低，且距离位置由80 mm减至20 mm时，失稳韧度降低约18.2%，断裂能降低约23.5%。
（4）对含不同数量水平裂缝缺陷的混凝土三点弯曲梁试件进行测试，结果表明断裂韧度和断裂能随着裂缝缺陷数量的增加而降低，且裂缝数量由0增加至3时，失稳韧度降低约21.9%，断裂能降低约20.4%。
（5）裂缝缺陷长度、位置和数量对混凝土断裂测试结果具有显著影响，后续研究还需对裂缝缺陷的宽度、角度等参数作进一步分析。同时，针对含裂缝缺陷的楔入劈裂试件和紧凑拉伸试件的断裂测试结果需进一步进行试验研究分析。
-
![]()
图 11 断裂参数随水平裂缝数量变化曲线
Figure 11. Fracture parameters versus number of horizontal cracks
表 1 试件设计参数
Table 1 Design parameters of specimens
试件编号 w/mm n h1/mm h2/mm TPB-W1-x 60 1 40 - TPB-W2-x 80 1 40 - TPB-W3-x 100 1 40 - TPB-W4-x 120 1 40 - TPB-H1-x 60 1 20 - TPB-H2-x 60 1 40 - TPB-H3-x 60 1 60 - TPB-H4-x 60 1 80 - TPB-N1-x 60 0 - - TPB-N2-x 60 1 40 - TPB-N3-x 60 2 40 20 TPB-N4-x 60 3 20 20 注：试件编号中，TPB代表三点弯曲梁试验；W，H，N分别代表含不同长度w、间距h1和h2以及数量n的水平裂缝缺陷的试件；x = 1，2，3，代表相同参数的试件各有3个。 
下载: 导出CSV
-
[1] 吴中如, 徐波, 顾冲时, 等. 大坝服役状态的合评判方法[J]. 中国科学: 技术科学,2012,55(8):2300-2312. (WU Zhongru, XU Bo, GU Chongshi, et al. Comprehensive evaluation methods for dam service status[J]. Science China Technological Sciences, 2012, 55(8): 2300-2312. (in Chinese) doi: 10.1007/s11431-012-4907-5 [2] KAPLAN M F. Crack propagation and the fracture of concrete[J]. Journal Proceedings, 1961, 58(11): 591-610.
[3] 尹阳阳, 胡少伟, 王宇航. 自重对混凝土三点弯曲梁断裂性能的影响[J]. 工程力学,2019,36(7):48-56, 108. (YIN Yangyang, HU Shaowei, WANG Yuhang. Influence of self-weight on the fracture properties of three-point bending concrete beams[J]. Engineering Mechanics, 2019, 36(7): 48-56, 108. (in Chinese) [4] LI T, XIAO J Z, ZHANG Y M, et al. Fracture behavior of recycled aggregate concrete under three-point bending[J]. Cement and Concrete Composites, 2019, 104: 103353. doi: 10.1016/j.cemconcomp.2019.103353
[5] XIAO J Z, SCHNEIDER H, DÖNNECKE C, et al. Wedge splitting test on fracture behaviour of ultra high strength concrete[J]. Construction and Building Materials, 2004, 18(6): 359-365. doi: 10.1016/j.conbuildmat.2004.04.016
[6] 胡少伟, 胡鑫, 范冰. 混凝土缺陷形状对楔入劈拉断裂性能的影响[J]. 水电能源科学,2019,37(8):110-113. (HU Shaowei, HU Xin, FAN Bing. Effect of defect shape on fracture characteristics of concrete wedge splitting[J]. Water Resources and Power, 2019, 37(8): 110-113. (in Chinese) [7] 胡少伟, 徐爱卿. 非标准混凝土楔入劈拉试件高宽比影响分析[J]. 硅酸盐学报,2015,43(10):1492-1499. (HU Shaowei, XU Aiqing. Effect analysis on fracture morphology of non-standard concrete wedge splitting tests by different height to width ratio[J]. Journal of the Chinese Ceramic Society, 2015, 43(10): 1492-1499. (in Chinese) [8] 李庆华, 种法澄, 张麒, 等. 改进的圆形紧凑拉伸法研究混凝土双G断裂参数[J]. 水利学报,2018,49(4):474-482. (LI Qinghua, CHONG Facheng, ZHANG Qi, et al. Study of double-G fracture parameters using modified round compact tension method[J]. Journal of Hydraulic Engineering, 2018, 49(4): 474-482. (in Chinese) [9] XU S L, REINHARDT H W. A simplified method for determining double-K fracture parameters for three-point bending tests[J]. International Journal of Fracture, 2000, 104(2): 181-209. doi: 10.1023/A:1007676716549
[10] XU S L, REINHARDT H W. Determination of double-K criterion for crack propagation in quasi-brittle fracture part I: experimental investigation of crack propagation[J]. International Journal of Fracture, 1999, 98(2): 111-149. doi: 10.1023/A:1018668929989
[11] 徐世烺, 赵国藩. 混凝土结构裂缝扩展的双K断裂准则[J]. 土木工程学报,1992,25(2):32-38. (XU Shilang, ZHAO Guofan. A double-K fracture criterion for the crack propagation in concrete structures[J]. China Civil Engineering Journal, 1992, 25(2): 32-38. (in Chinese) [12] 中华人民共和国国家发展和改革委员会. 水工混凝土断裂试验规程: DL/T 5332—2005[S]. 北京: 中国电力出版社, 2006. National Development and Reform Commission. Norm for fracture test of hydraulic concrete: DL/T 5332—2005[S]. Beijing: China Electric Power Press, 2006. (in Chinese)
[13] 胡少伟, 胡鑫. 含空洞缺陷混凝土试件楔入劈拉性能分析[J]. 水利水运工程学报,2017(1):1-9. (HU Shaowei, HU Xin. Experimental studies and performance analysis of wedge splitting for concrete specimens with cavity defects[J]. Hydro-Science and Engineering, 2017(1): 1-9. (in Chinese) [14] 胡少伟, 尹阳阳, 王强. 双缝混凝土三点弯曲梁断裂性能试验[J]. 河海大学学报(自然科学版),2019,47(3):265-270. (HU Shaowei, YIN Yangyang, WANG Qiang. Experimental study on the fracture properties of three-point bending concrete beam with double cracks[J]. Journal of Hohai University (Natural Sciences), 2019, 47(3): 265-270. (in Chinese) [15] 孙国有, 薛继良, 兰清生, 等. 空洞扩张与I-II复合型裂纹的断裂参量[J]. 浙江大学学报(自然科学版),1994,28(1):1-8. (SUN Guoyou, XUE Jiliang, LAN Qingsheng, et al. Void growth and fracture criteria of cracks of mixed I and II modes[J]. Journal of Zhejiang University (Natural Science), 1994, 28(1): 1-8. (in Chinese) [16] RILEM Technical Committee (50-FMC). Determination of the fracture energy of mortar and concrete by means of three-point bend tests on notched beams[J]. Materials and Structures, 1985, 18(4): 287-290.
-
期刊类型引用(4)
1. 张继良，王颖，江泽安. 基于机器视觉的水利枢纽工程混凝土缺陷红外勘测方法. 水利技术监督. 2024(09): 10-13+21 . 
百度学术
2. 孙拴虎，李琪，张新蕾，符惠萍，张悦，韩小龙. 基于道床板温度裂缝的治理探究. 甘肃科技纵横. 2023(02): 38-40+66 . 百度学术
3. 肖艳，张从从，韦爱群. 水闸中出现的典型问题及对应措施研究. 陕西水利. 2021(04): 204-206 . 百度学术
4. 江宏玲. 质量监管信息化系统应用于现浇板裂缝防治的探究. 工程质量. 2021(06): 34-36+41 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 861
- HTML全文浏览量: 436
- PDF下载量: 21
- 被引次数: 8
