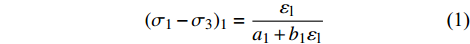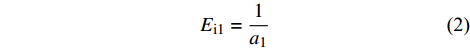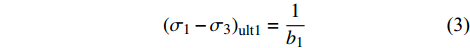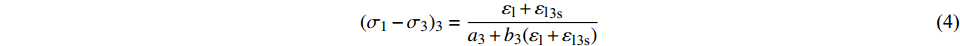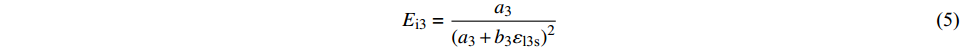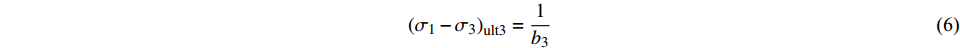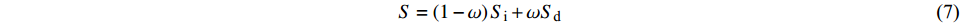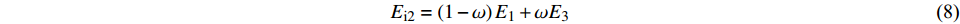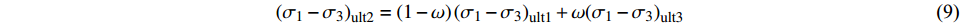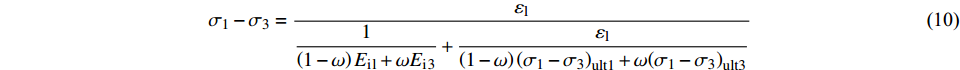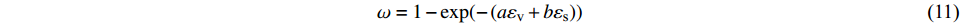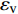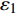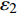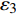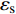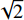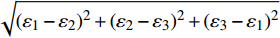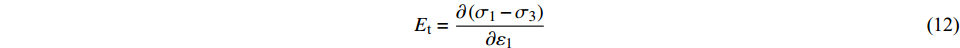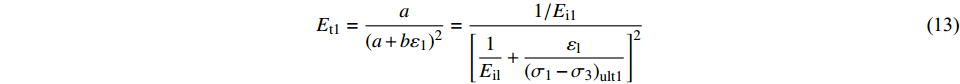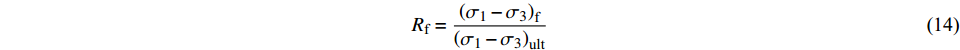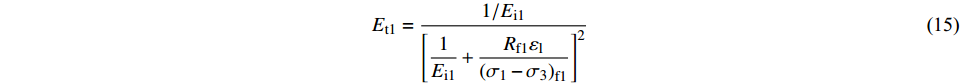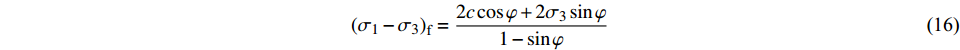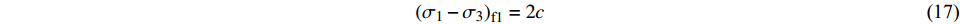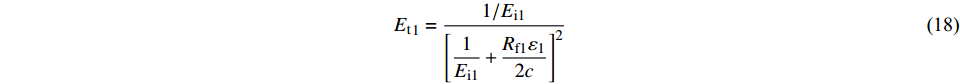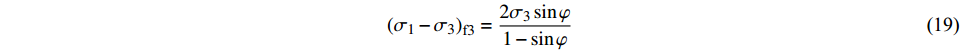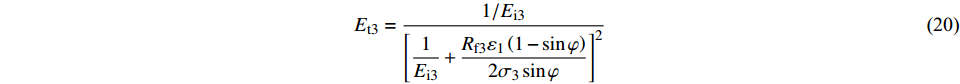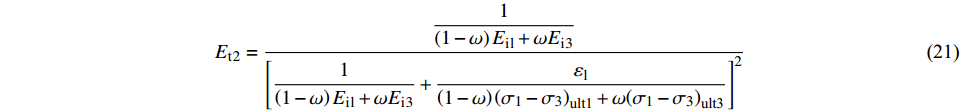Research on modified Duncan-Chang Model for strong structured clay
-
摘要: 土体的力学特性受结构性影响十分显著,结构性越强,破坏后变形越大,对实际工程影响越显著。目前对结构性土的特殊工程性质已有广泛认识,但如何用数学方法准确描述其强度和变形间的关系仍是主要研究内容。对分布在云南昭通地区的强结构性黏土进行了试验研究,结果表明:其结构屈服应力高达800 kPa,属于典型的强结构性土。根据常规三轴试验的应力-应变关系,将强结构性黏土的剪切变形划分为结构未破坏阶段、结构逐渐破坏阶段和结构完全破坏阶段;基于破坏过程,对传统邓肯-张模型进行修正,引入损伤比参数,建立适用于强结构性黏土的修正邓肯-张本构模型。对模型中的初始剪切模量、主应力差渐进值和剪切模量参数进行推导分析,各参数值与试验的土体剪切变形规律相符合;对已有结构性土的试验数据进行拟合分析,结果表明该修正模型可以较好地描述强结构性黏土的应力-应变特性规律。Abstract: The mechanical properties of soil are significantly influenced by the structure: the stronger the structure is, the greater the deformation of the soil damage is, and the more significant the impact on the actual project is. At present, the special engineering properties of structural soil have been widely understood, but how to accurately describe the relationship between strength and deformation by mathematical methods is still the main research content. In this research, an experimental study is carried out on the strong structural clay distributed in Zhaotong, Yunnan. The results show that the structural yield stress is as high as 800 kPa, which is a typical strong structured soil. According to the stress-strain relationship of the conventional triaxial tests, the shear deformation of strong structural clay is divided into structural non-failure stage, structural gradual failure stage and structural complete failure stage. Based on the failure process, the traditional Duncan-Chang model is modified and the damage ratio parameter is introduced to establish a modified Duncan-Chang constitutive model suitable for strong structural clay. The initial shear modulus, the asymptotic value of the principal stress difference and the shear modulus parameters in the model are deduced and analyzed, and the parameter values are consistent with the shear deformation law of the experimental soil. Through fitting and analyzing the experimental data of existing structured soil, the results show that the modified model can better describe the stress-strain characteristics of strong structural clay.
-
结构性是天然沉积土的固有特性,主要包括矿物组分、土颗粒的大小和排列方式、孔隙的大小和分布及单元间的连接方式。结构性的强弱体现于土体结构性破坏前后力学性质的差异,结构性未破坏的土体具有良好的工程性质,当结构性破坏后,其强度大幅度减小,变形量急剧增加,对实际工程产生很大影响。
目前对结构性土的工程特性已有一定的认识,但如何用数学方法准确描述其强度和变形的关系仍是目前的主要研究内容。不少学者针对结构性土,从不同角度出发建立了相关的本构模型并提出一些新的结构性参数。如沈珠江[1]基于损伤力学概念,提出了考虑土体结构性破损过程的损伤力学模型和非线性损伤力学模型;谢定义等[2]基于结构性土的一维固结压缩试验提出了反映土体结构性的综合结构势(mp);刘恩龙等[3]基于大量结构性土的强度试验数据,引入剪切抗力贡献参数,并考虑土体破损机理的二元介质模型概念,建立了结构性土的强度准则;Kavvadas等[4]基于已有的边界模型概念,引入土体结构性新参数,建立了结构性土的本构模型;陶虎等[5]以构度指标定量评价了黄土结构强弱及结构性参数随加载变化的规律,将结构性参数引入邓肯-张模型中,建立了预测结构性土发展的本构模型。
建立土的本构模型是为了更好反映土体的强度和变形关系。邓肯-张模型因土体参数容易确定,且能较好反映土体应力-应变关系而被广泛应用于数值分析,但由于该模型是基于重塑土建立的,并不适用于结构性土体。一些学者对邓肯-张模型进行了改进:王立忠等[6]将结构性土体的剪切变形特性分为3个线性变化阶段,建立了修正邓肯-张模型,用以反映结构性土的应力-应变关系;陈昌禄等[7]引入文献[2]提出的综合结构势概念、考虑剪应力和球应力的影响,对适用于结构性黄土的邓肯-张修正模型进行了研究;杨爱武等[8]考虑了围压和偏应力的影响,建立了适用于天津海积软土的修正邓肯-张模型;谷建晓等[9]基于结构性邓肯-张模型,提出了一种计算损伤参数的方法,以反映红黏土应力-应变在不同阶段的发展规律;孙谷雨等[10]建立了以温度、围压为影响因素的冻结粉质黏土邓肯-张本构模型,能较好反映不同围压、温度条件下粉质黏土的强度和变形特性;张琰等[11]研究了压实黏土在三轴压缩、拉伸及从压缩到反向拉伸状态下的应力应变特性,并在此基础上对邓肯-张模型的应用范围进行扩展。
以上相关修正模型主要针对土体的应力-应变关系进行,对相关参数的适用性并未进行深入分析。另外,土体是在天然条件下沉积形成的,其结构性受矿物成分、颗粒大小、沉积年代和上覆荷载等多种因素的影响[12],不同地区土体的结构性有显著差异,所表现出的力学特性也有所不同。因此,本文针对昭通地区广泛分布的强结构性黏土进行一系列室内试验,分析一维固结压缩特性和三轴剪切特性,基于强结构性黏土的应力-应变关系,引入损伤比概念,对传统邓肯-张模型进行修正,使其能更好描述强结构性黏土的应力-应变关系,并对修正后模型相关参数的适用性进行了进一步推导分析。
1. 试验方法及试验结果
试验用土取自昭通市昭阳区,取样深度约20 m,属第三系湖积层。依据JTG 3430—2020《公路土工试验规程》[13]对土样进行了基本物理性质、矿物组分和粒径的测定,根据规范GB 50021—2001《岩土勘察规范》[14]可判定为黏土。为了分析土体的力学特性,对试样进行了一维固结压缩试验和常规三轴剪切试验。一维固结压缩试验采用WG型三联杠杆一维固结仪加载方式按照JTG 3430—2020《公路土工试验规程》[13]采用分级加载,施加1.0 kPa 荷载使试样压缩稳定,稳定后施加第一级荷载,加荷比为1∶1。固结压力按 12.5→25→50→100→200→400→800→1 000→1 200→1 400→1 600→3 200 kPa的顺序逐级加载,每级荷载持续时间为24 h。三轴剪切试验采用三轴应变式控制仪,使试样在围压分别为50、100、200、400、600、800、1 000、1 200和1 400 kPa下固结,试验步骤参照JTG 3430—2020《公路土工试验规程》[13]进行。
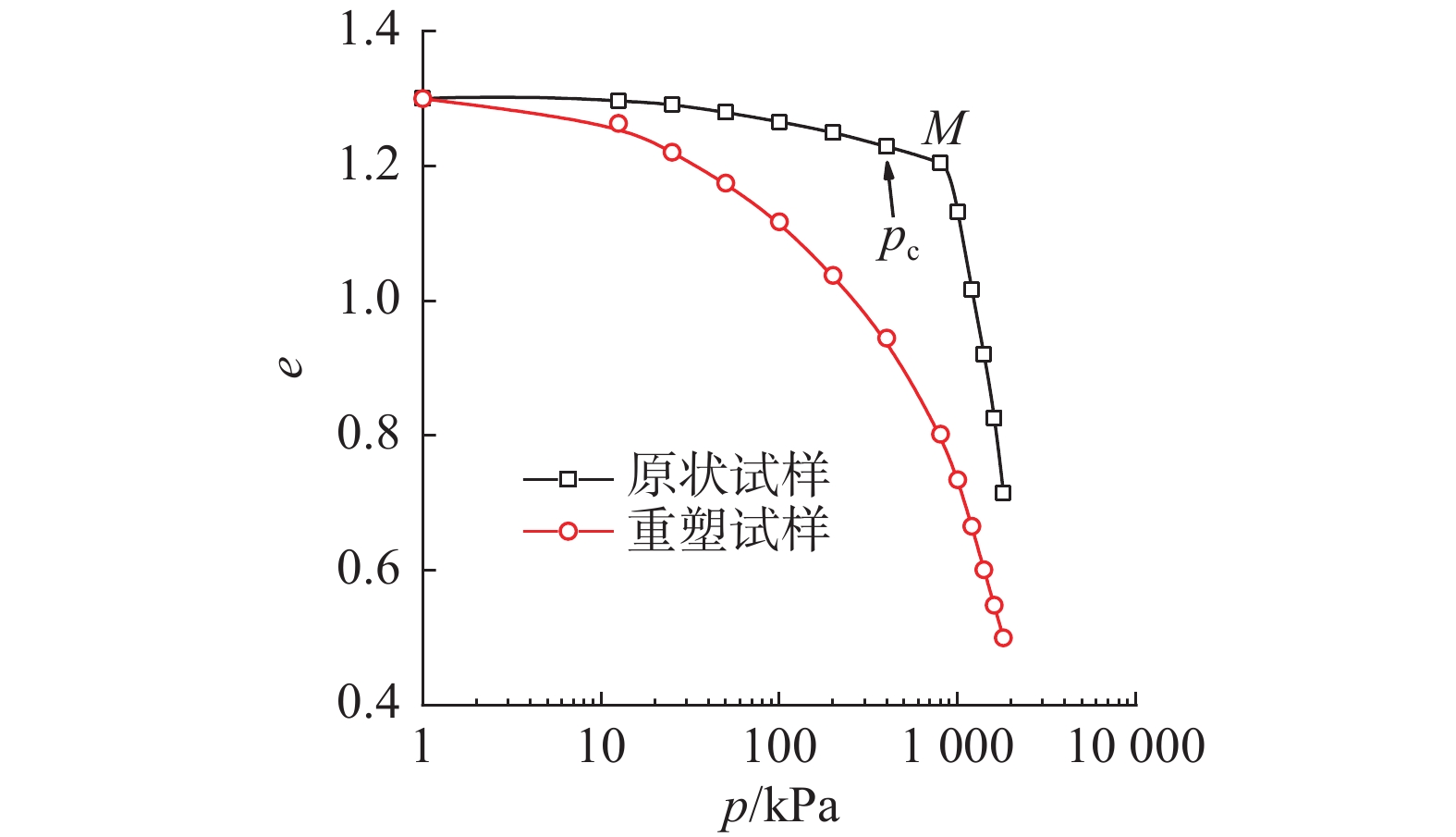
原状土和重塑土的一维压缩曲线如图1所示。由图1可以看出,原状土的e-lgp曲线可近似看作由两条相交直线组成,交点处对应的固结压力约为800 kPa;在固结压力小于800 kPa时,单位应力增量下孔隙体积变化量较小,当固结压力大于800 kPa时,单位应力增量下土体孔隙体积急剧减小。重塑土的e-lgp曲线为一条连续光滑的曲线,无明显的转折点,且位于原状土e-lgp曲线下方。随着固结压力的增加原状土的e-lgp曲线与重塑土逐渐趋于重合。
已有研究显示该区域晚中新世到上新世期间土体的沉积环境相对稳定[15],这表明土体的先期固结压力与已有上覆土重接近,且根据取样深度可知,土体的上覆土压力Pc≈400 kPa,远远小于e-lgp曲线交点处对应的固结压力800 kPa(图1)。综合以上分析可知:该黏土为一种典型的强结构性土。图中交点M对应的固结压力即为土体的结构屈服应力,约为800 kPa。因此,在小于结构屈服应力的固结压力作用下,土的强结构性使得土体在外荷载作用下产生的变形量十分微小,对应的孔隙变化量也非常小,结构破坏前的压缩指数cc约为0.03;当固结压力大于结构屈服应力后,支撑土体框架的结构发生破坏,土体孔隙体积在较小的应力增量下大幅度降低,e-lgp曲线逐渐趋于重塑土,此时的土体压缩指数cc'约为1.4,是结构性破坏前的4倍多。洪振舜等[16]对日本强结构性硅藻土的研究也得到了类似结论。
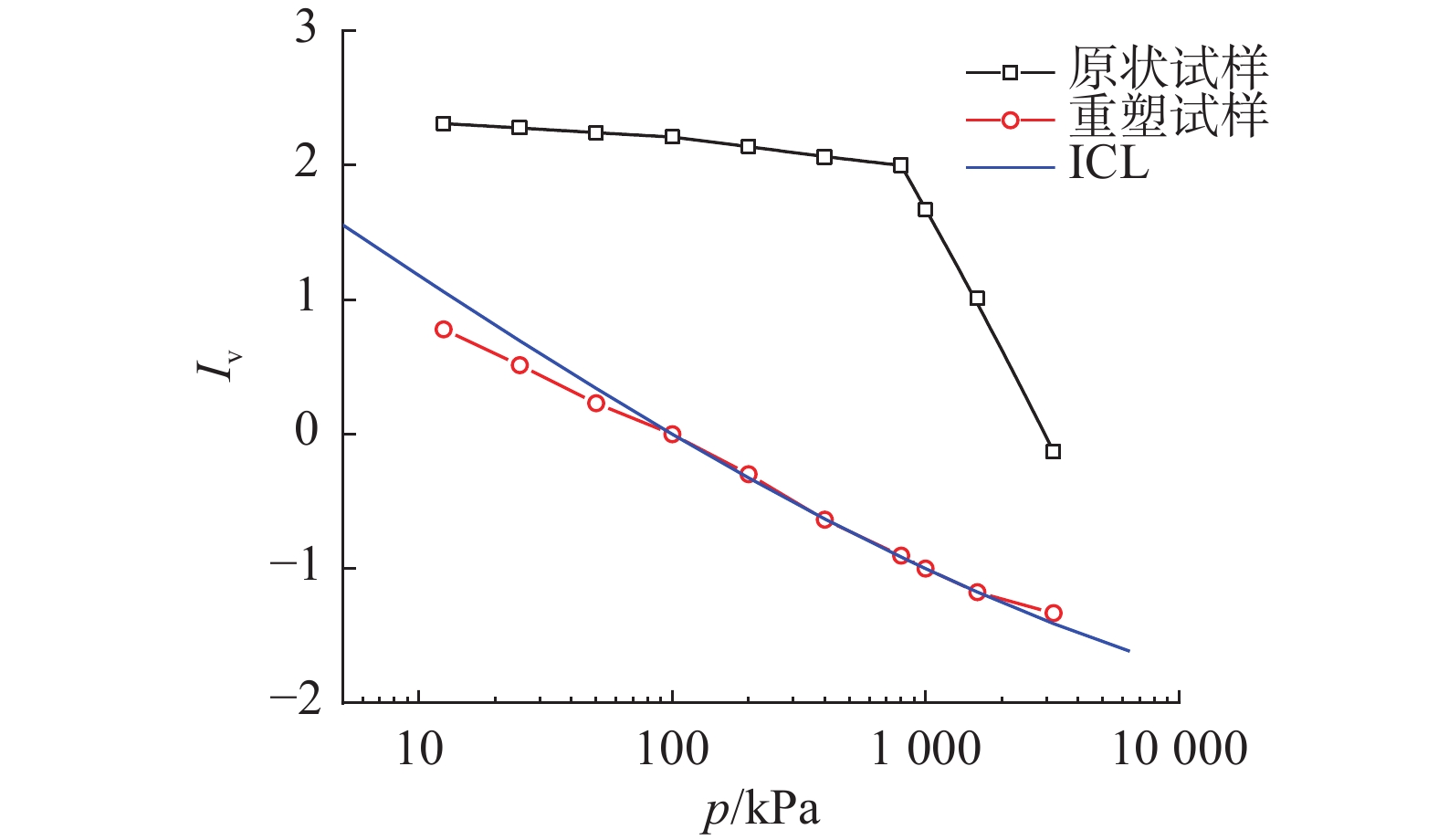
为进一步分析该黏土结构性强弱,利用Burland[17]提出的固有压缩曲线(ICL)来评估该土的结构性。强结构性黏土的原状试样和重塑试样的Iv-lgp曲线如图2所示。可以看出,重塑试样的孔隙指数可在固结压力大于100 kPa后与固有压缩曲线(ICL)基本重合。由于强结构性的影响,原状试样的Iv-lgp曲线位于ICL曲线上方,固结压力小于800 kPa时土体孔隙指数变化量较小,当固结压力大于800 kPa后,孔隙指数显著减小,且逐渐趋于ICL曲线,这表明该黏土具有较强的结构性。
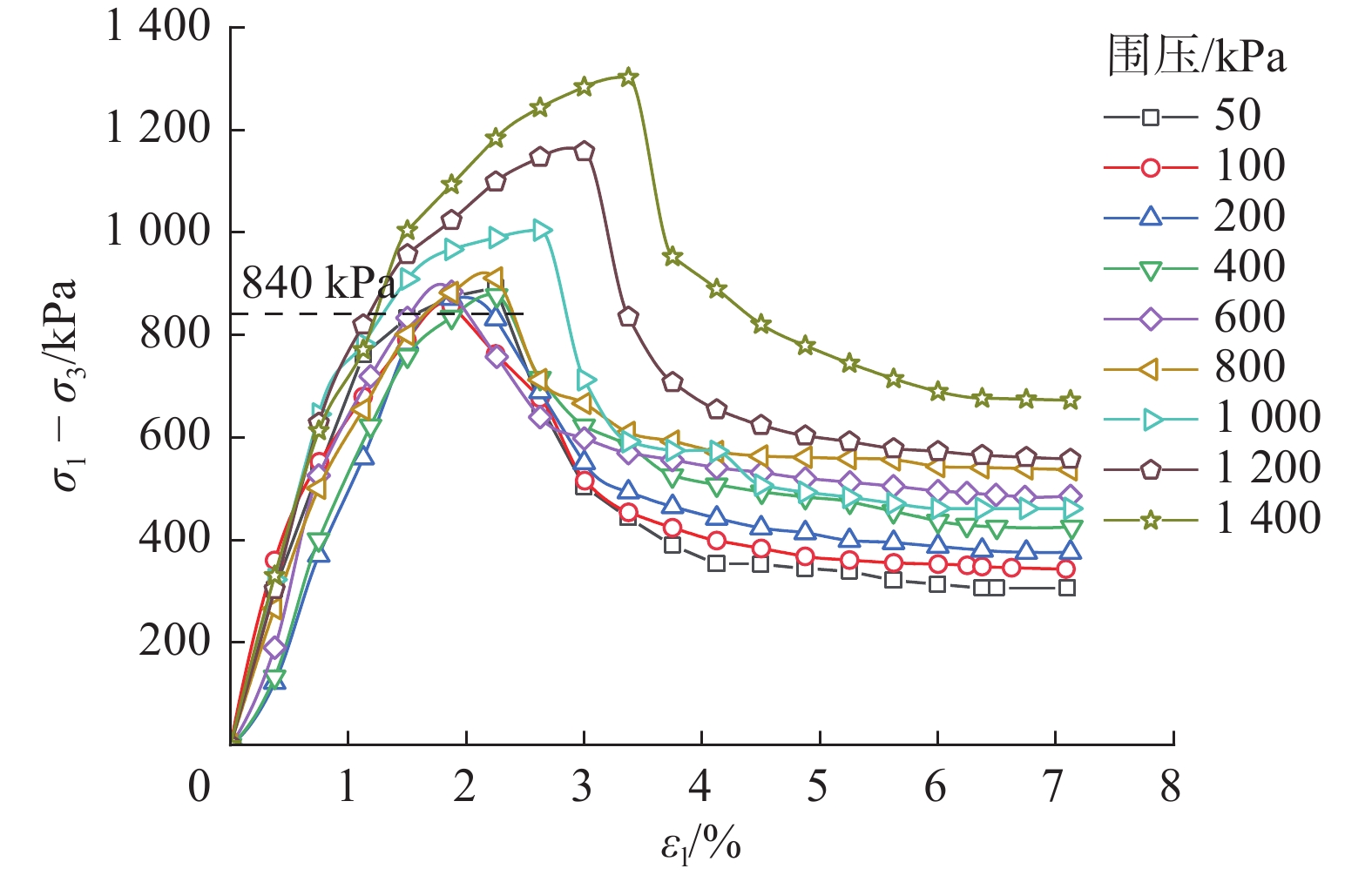
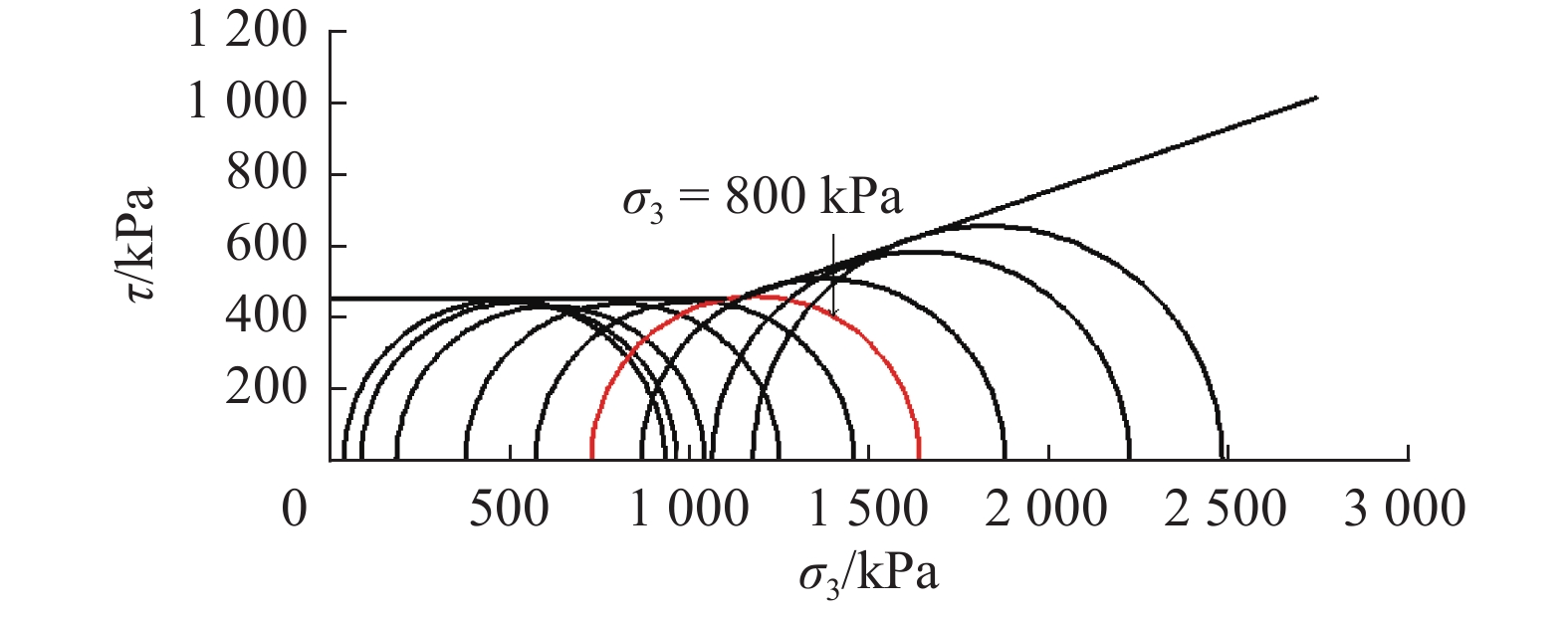
常规三轴剪切试验得到原状土在不同围压下强结构性黏土的应力-应变关系见图3。由图3可见,加载初期,试验在不同围压下的应力随应变的增加几乎呈线性增大,当应力增加到峰值后,应力随应变急剧减小,随着应变的继续增加,应力逐渐趋于平稳,应力-应变关系曲线均为应变软化型;压力小于等于800 kPa时,各级围压下试样的主应力差峰值在850 kPa左右,当固结围压大于800 kPa后,主应力差峰值随固结围压的增加而增大。图4为强结构性黏土的总应力强度包线图,可见强结构性黏土的强度包线由两条直线组成,当固结压力小于等于800 kPa时,剪切强度随固结围压的增加保持不变,强度包线为一条平行于x轴的直线,当固结压力超过800 kPa后,剪切强度随固结围压的增加而增大,强度包线为一条过原点的斜直线。
由于土体结构屈服应力为800 kPa,当固结围压小于结构屈服强度时,试样破坏时的剪切强度取决于结构性所产生的抵抗能力,与固结围压无关,破坏时对应的主应力差峰值为定值,强度包线为水平直线;当固结压力大于结构屈服应力值时,土体的结构性破坏,剪切强度随固结围压的增加而增大,强度包线为一条过原点的斜直线。常规三轴剪切试验结果也再次证明了该土具有较强的结构性。
2. 考虑强结构性的修正邓肯-张模型研究
2.1 基于邓肯-张模型的昭通黏土应力-应变关系研究
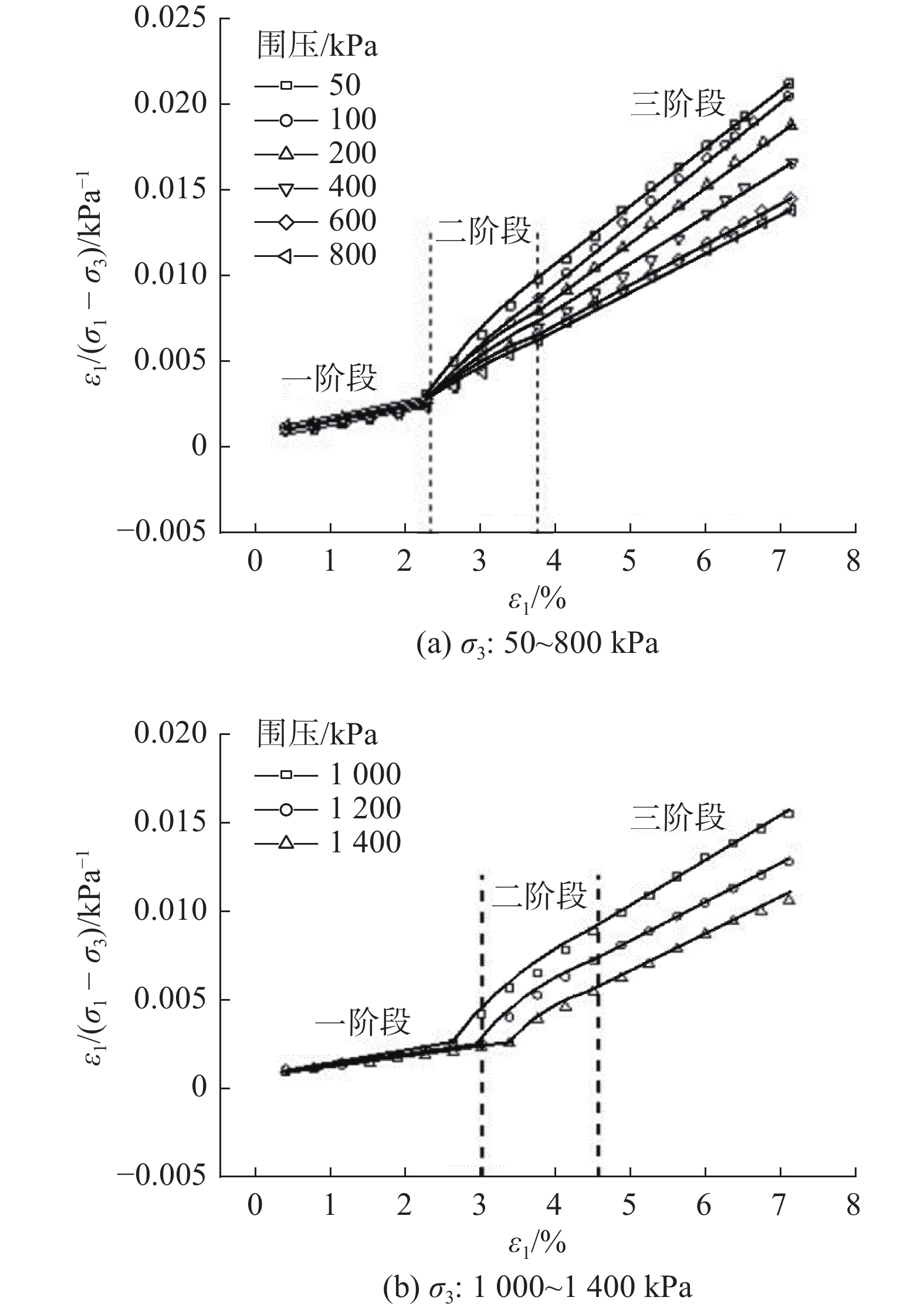
图5为强结构性黏土εl /(σ1−σ3)-εl关系曲线。由图5可知:当σ3≤结构屈服应力时,土体破坏对应的应变均为定值(约为2.25%);当σ3>结构屈服应力时,土体破坏对应的应变随固结压力的增加而右移。此外,由图5还可以发现,无论围压是否大于土体的固结屈服应力,强结构黏土的εl /(σ1−σ3)-εl关系曲线均不是由单一直线构成。结合结构性土体实际破坏规律,将土体的εl /(σ1−σ3)-εl关系曲线划分为3个阶段。第一阶段为结构未破坏阶段,此时土体的变形为弹性变形,土的应力-应变关系较为明确,εl /(σ1−σ3)-εl关系曲线为直线;第二阶段为结构性破坏阶段,主应力差值陡降,土体产生的变形为弹塑性变形,此时的应力随应变的增加呈非线性变化,εl /(σ1−σ3)-εl关系曲线呈类似指数函数变化;第三阶段为土体结构性完全破坏后,土体的变形主要为塑性变形,对应εl/(σ1−σ3)-εl关系曲线为一条直线。传统邓肯-张模型仅适用于εl /(σ1−σ3)-εl曲线为单一直线的应力-应变关系。强结构性黏土并不适用于邓肯-张模型[18]。为了使邓肯-张模型能更好地适用于强结构性黏土,有必要对其进行修正。
根据图5的划分结果,把强结构性黏土的应力-应变关系分为3个阶段进行分析处理,其εl/(σ1−σ3)-εl关系简化图如图6所示。引入损伤比概念,对邓肯-张模型进行修正,建立适用于强结构性黏土的本构模型。具体方法如下:
(1)在荷载作用下,当土体处于第一阶段时,强结构性黏土的应力-应变关系为与y轴相交的斜直线,此时,该阶段可以用传统的邓肯-张模型进行表示,即:
$$ {({\sigma _1} - {\sigma _3})_1} = \frac{{{\varepsilon _{\text{l}}}_{}}}{{{a_1} + {b_1}{\varepsilon _{\text{l}}}_{}}} $$ (1) 式中:(σ1−σ3)1为第一阶段的主应力差值;εl为应变值;a1和b1分别为第一阶段εl/(σ1−σ3)-εl关系曲线对应的截距和斜率。
根据土体应力应变双曲线关系[19],第一阶段的初始剪切模量Ei1和主应力差渐进值(σ1−σ3) ult1可以表示为:
$$ {E_{{\text{i}}1}} = \frac{1}{{{a_1}}} $$ (2) $$ {\left( {{\sigma _1} - {\sigma _3}} \right)_{{\text{ult}}1}} = \frac{1}{{{b_1}}} $$ (3) (2)由图6可以看出,土体第三阶段直线斜率较第一阶段大,此时土体的截距为负值,即当εl →∞时,a3<0,根据E3=1/a3计算得出的土体初始剪切模量为负值,与实际不符。基于此,第三阶段土体可单独进行处理分析。根据常规三轴试验的应力-应变关系曲线可明确得出土体初始进入第三阶段时对应的应变εl3s,该值即为常数。因此,第三阶段的应变可以表示为εl3=εl1+εl3s,则土体的应力-应变关系为:
$$ {({\sigma _1} - {\sigma _3})_3} = \frac{{{\varepsilon _{\text{l}}} + {\varepsilon _{\text{l}}}_{{\text{3s}}}}}{{{a_3} + {b_3}({\varepsilon _{\text{l}}} + {\varepsilon _{\text{l}}}_{{\text{3s}}})}} $$ (4) 当εl→0时,根据式(4)可得出土体处于第三阶段的初始剪切模量:
$$ {E_{{\text{i}}3}} = \frac{{{a_3}}}{{{{\left( {{a_3} + {b_3}{\varepsilon _{{\text{l3s}}}}} \right)}^2}}} $$ (5) 式(4)可以改写为:
$$ {({\sigma _1} - {\sigma _3})_3} = \frac{1}{{\dfrac{{{a_3}}}{{{\varepsilon _{\text{l}}} + {\varepsilon _{\text{l}}}_{3{\text{s}}}}} + {b_3}}} $$ 当ε1→∞时,可得第三阶段土体的主应力差渐进值:
$$ {\left( {{\sigma _1} - {\sigma _3}} \right)_{{\text{ult}}3}} = \frac{1}{{{b_3}}} $$ (6) (3)对于第二阶段,土体结构处于逐渐破坏阶段,是由原状土到重塑土的过渡阶段,该阶段土体的εl/(σ1−σ3) 随εl呈现非线性变化,根据双曲线方法无法得出该阶段土体的初始剪切模量和主应力差渐进值。对此,引入土体损伤比概念[6],即土体在外荷载作用下发生的变形过程可以看作是由原状土体向重塑土体变化的过程,而整个过程中土体的力学性质可由原状试样和重塑试样的特性反映,表达式如下:
$$ S = \left( {1 - \omega } \right){S_{\text{i}}} + \omega {S_{\text{d}}} $$ (7) 式中:ω为损伤比,即为损伤部分在土体中所占的比重;S为原状土过渡到损伤土(扰动土、重塑土)的特性;Si表示原状土体的特性;Sd表示损伤土(扰动土、重塑土)的特性。
根据式(5)可知,对于强结构性黏土,原状土体过渡到重塑土的初始剪切模量Ei2可表示为:
$$ {E_{{\text{i}}2}} = \left( {1 - \omega } \right){E_1} + \omega {E_3} $$ (8) 第二阶段的主应力差渐进值(σ1−σ3) ult2可表示为:
$$ {\left( {{\sigma _1} - {\sigma _3}} \right)_{{\text{ult}}2}} = \left( {1 - \omega } \right){\left( {{\sigma _1} - {\sigma _3}} \right)_{{\text{ult}}1}} + \omega {\left( {{\sigma _1} - {\sigma _3}} \right)_{{\text{ult}}3}} $$ (9) 因此,第二阶段的应力-应变关系曲线可表示为:
$$ {\sigma _1} - {\sigma _3} = \dfrac{{{\varepsilon _{\rm{l}}}}}{{\dfrac{1}{{\left( {1 - \omega } \right){E_{\rm{i}}}_{\rm{l}} + \omega {E_{\rm{i}}}_{\rm{3}}}} + \dfrac{{{\varepsilon _{\rm{l}}}}}{{\left( {1 - \omega } \right){{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{ult}}1}} + \omega {{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{ult}}3}}}}}} $$ (10) 沈珠江[1]建议土体的损伤比ω可按下式计算:
$$ \omega = 1 - \exp ( - \left( {a{\varepsilon _{\text{v}}} + b{\varepsilon _{\text{s}}}} \right) )$$ (11) 式中:
$ {\varepsilon }_{\mathrm{v}} $ =$ {\varepsilon }_{1} $ +$ {\varepsilon }_{2} $ +$ {\varepsilon }_{3} $ ,$ {\varepsilon }_{\mathrm{s}} $ =(1/$ \sqrt{2} $ )$ \sqrt{{({\varepsilon }_{1}-{\varepsilon }_{2})}^{2}+{({\varepsilon }_{2}-{\varepsilon }_{3})}^{2}+{({\varepsilon }_{3}-{\varepsilon }_{1})}^{2}} $ ,其中参数a和b可通过室内一维压缩试验和无侧限抗压试验进行测定。初始剪切模量为土体在剪切开始时的应力增量和应变增量的比值。第一阶段土体变形以弹性为主,单位荷载增量下土体的变形增量较小,因此其初始剪切模量较大;第三阶段土体结构与重塑土结构类似,土体变形以塑性为主,因此该阶段土体的初始剪切模量较小;第二阶段土体处于结构性破坏而未完全破坏的过程,因此该阶段土体的初始剪切模量较第一阶段小但大于第三阶段,即:Ei1> Ei2 >Ei3,与实际土体的剪切模量相符。
土体的主应力差渐进值为应变趋近于无穷大时主应力差值可达到的最大值。(σ1−σ3)ult1为第一阶段的主应力差渐进值,即为土体弹性范围内可达到的最大主应力差;(σ1−σ3)ult2为第二阶段的主应力差渐进值,即为土体在结构性逐渐破坏过程中可达到的最大主应力差;第三阶段的主应力差渐进值为(σ1−σ3)ult3,可认为该值为土体结构性完全破坏后的残余强度极限值。
2.2 修正邓肯-张模型各阶段剪切模量对比
土体的剪切模量为应力增量与应变增量的比值,可表示为:
$$ {E_{\text{t}}} = \frac{{\partial \left( {{\sigma _1} - {\sigma _3}} \right)}}{{\partial {\varepsilon _1}}} $$ (12) 土体的压缩剪切破坏过程,是原状土向重塑土转变的过程。对应土体各阶段的剪切模量也有所差异。对于土体第一阶段,其剪切模量Et1可以表示为:
$$ {E_{{\rm{t}}1}} = \dfrac{a}{{{{\left( {a + b{\varepsilon _1}} \right)}^2}}} = \dfrac{{1/{E_{{\rm{i}}1}}}}{{{{\left[ { {\dfrac{1}{{{E_{{\rm{il}}}}}}} + \dfrac{{{\varepsilon _{\rm{l}}}}}{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{ult}}1}}}}} \right]}^2}}} $$ (13) 整个剪切过程中土体的破坏比可表示为:
$$ {R_{\text{f}}} = \frac{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{\text{f}}}}}{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\text{ult}}}}}} $$ (14) 式中:(σ1−σ3)f为土体破坏时的主应力差值。
将破坏比代入式(13),则第一阶段土体剪切模量可以表示为:
$$ {E_{{\rm{t1}}}} = \dfrac{{1/{E_{{\rm{i}}1}}}}{{{{\left[ { {\dfrac{1}{{{E_{{\rm{i}}1}}}}} + \dfrac{{{R_{{\rm{f}}1}}{\varepsilon _{\rm{l}}}}}{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{f1}}}}}}} \right]}^2}}} $$ (15) 根据摩尔-库伦破坏准则可知,土体发生破坏时,主应力差可以表示为:
$$ {\left( {{\sigma _1} - {\sigma _3}} \right)_{\text{f}}} = \frac{{2c\cos \varphi + 2{\sigma _3}\sin \varphi }}{{1 - \sin \varphi }} $$ (16) 土体处于第一阶段时,强度包络线为一条平行于x轴的直线,此时土体破坏时的主应力差值只与土体黏聚力有关,可以表示为:
$$ {\left( {{\sigma _1} - {\sigma _3}} \right)_{{\text{f}}1}} = 2c $$ (17) 将式(17)代入式(15),则第一阶段剪切模量为:
$$ {E_{\rm{t}}}_1 = \dfrac{{1/{E_{{\rm{i}}1}}}}{{{{\left[ { {\dfrac{1}{{{E_{{\rm{i1}}}}}}} + \dfrac{{{R_{{\rm{f}}1}}{\varepsilon _1}}}{{2c}}} \right]}^2}}} $$ (18) 当土体处于第三阶段时,摩尔应力圆随围压的增加而增大,对应土体的强度包络线为一条过原点的直线,表明此时土体已经进入重塑土阶段,此时土体破坏时的主应力差可以表示为:
$$ {\left( {{\sigma _1} - {\sigma _3}} \right)_{{\text{f}}3}} = \frac{{2{\sigma _3}\sin \varphi }}{{1 - \sin \varphi }} $$ (19) 因此,强结构性土体的第三阶段剪切模量可以表示为:
$$ {E_{{\rm{t3}}}} = \dfrac{{1/{E_{{\rm{i3}}}}}}{{{{\left[ { {\dfrac{1}{{{E_{{\rm{i}}3}}}}} + \dfrac{{{R_{{\rm{f}}3}}{\varepsilon _1}\left( {1 - \sin \varphi } \right)}}{{2{\sigma _3}\sin \varphi }}} \right]}^2}}} $$ (20) 土体第二阶段,是原状土过渡到重塑土阶段,由于各级围压跨度较大,第二阶段在包线图中并不明显。因此,根据式(10)可得到土体在第二阶段的剪切模量:
$$ {E_{\text{t}}}_2 = \dfrac{{\dfrac{1}{{\left( {1 - \omega } \right){E_{\text{i}}}_{\text{l}} + \omega {E_{\text{i}}}_3}}}}{{{{\left[ {\dfrac{1}{{\left( {1 - \omega } \right){E_{\text{i}}}_{\text{l}} + \omega {E_{\text{i}}}_3}} + \dfrac{{{\varepsilon _{\text{l}}}}}{{\left( {1 - \omega } \right){{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\text{ult1}}}} + \omega {{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\text{ult3}}}}}}} \right]}^2}}} $$ (21) 各阶段土体的剪切模量是逐渐变化的。第一阶段土体结构性未发生破坏,其应力随应变呈线性增大而后开始减缓,该阶段土体的剪切模量随应变的增加逐渐减小;第二阶段土体结构性逐渐破坏,由原状土向重塑土过渡,随应变增加土体强度开始降低,此时土体的剪切模量值也逐渐降低;第三阶段土体结构性完全破坏,应力随应变增加趋于定值,其剪切模量逐渐减小。相较于邓肯-张模型得出的剪切模量计算方法,根据本修正方法得出的剪切模量值更符合土体剪切破坏过程中土体的变形规律。
3. 修正邓肯-张模型适用性重塑土验证
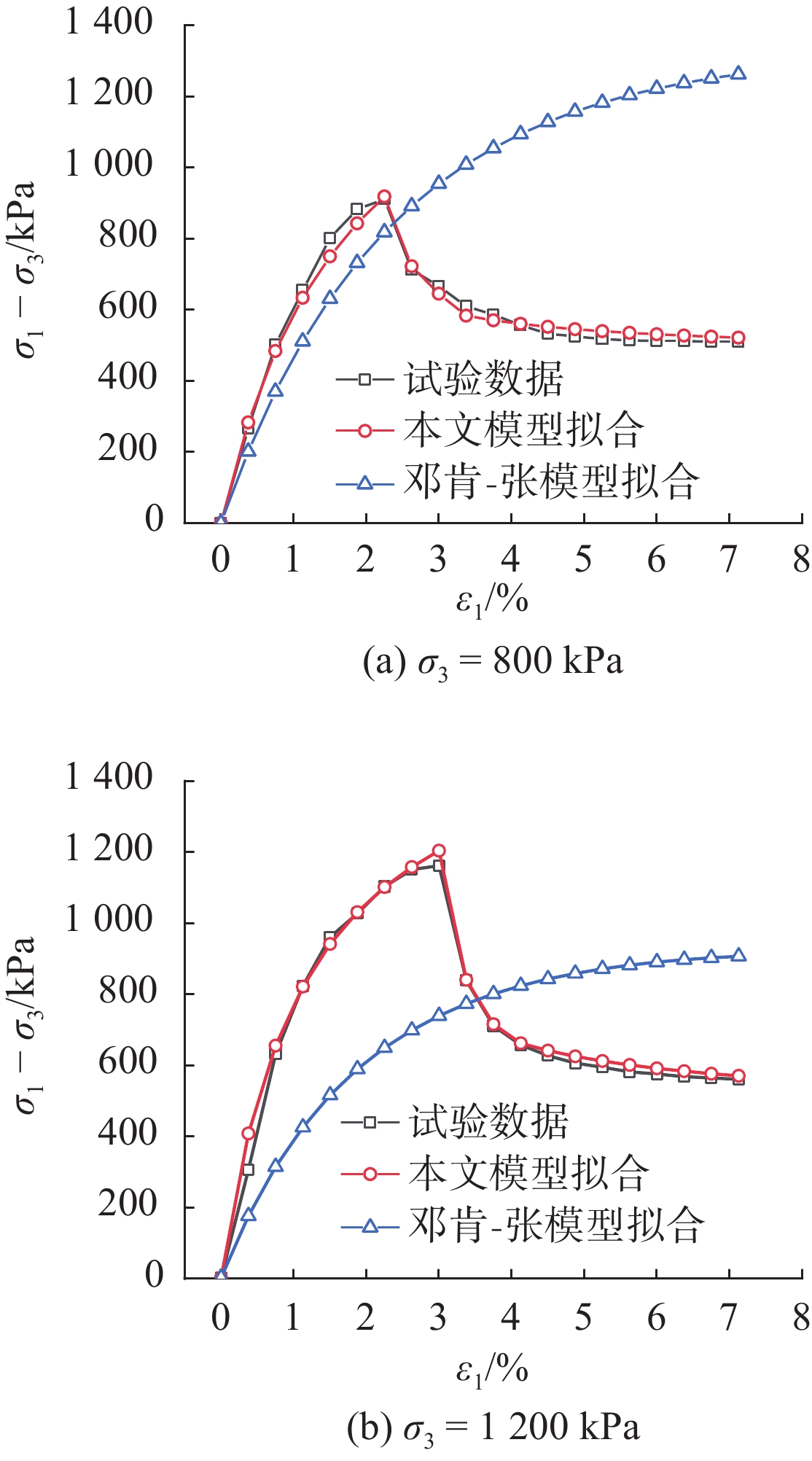
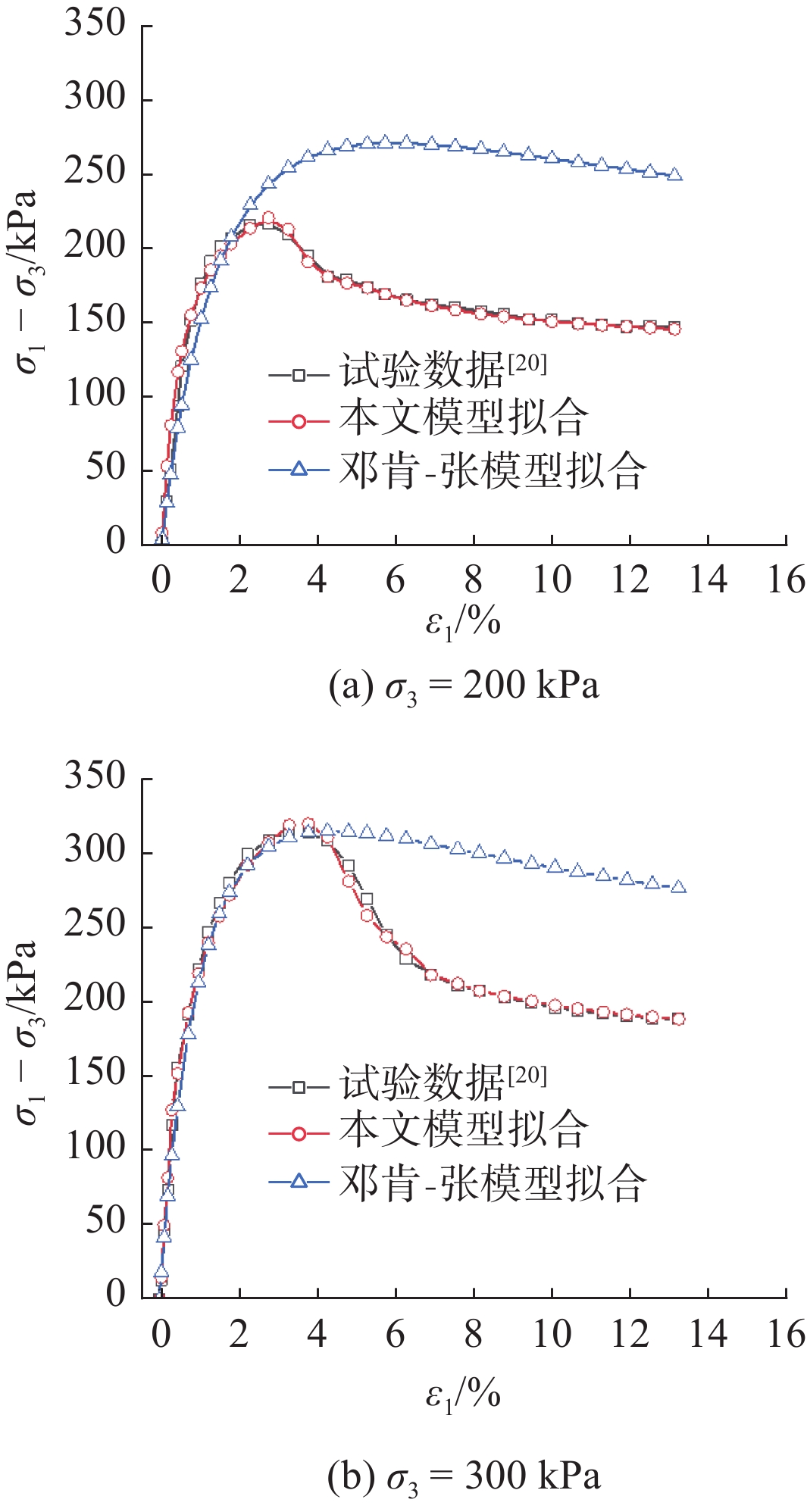
为了验证该模型的适用性,分别以湛江组结构性黏土[20]、火山泥岩[21]和本文结构性黏土的常规三轴试验试验结果为基础,选择两个不同围压下的应力-应变关系曲线,将本文邓肯-张修正模型与邓肯-张模型和试验实测数据进行拟合对比分析,如图7~9所示。根据拟合情况可以看出:(1)对于昭通强结构性黏土,在土体结构破坏前后,邓肯-张模型拟合的应力应变-关系与试验实测数据有较大差距,本模型拟合结果与试验数据具有较高的符合度;(2)对于湛江结构性黏土,在土体结构破坏前,本文修正模型和邓肯-张模型拟合结果与实测数据都具有较好的拟合度,但结构破坏后,本文修正模型拟合度更高;(3)火山泥岩在围压3 000 kPa时的拟合情况与湛江黏土类似,围压为9 500 kPa时,土体结构破坏前邓肯-张模型拟合度较本文修正模型拟合度低,土体结构破坏后两个模型的拟合度接近。总体而言,本文修正模型较邓肯-张模型更适用于强结构性黏土。
4. 结 语
本文以昭通强结构性黏土为研究对象,进行了一维固结压缩试验和常规三轴剪切试验,确定了该黏土的结构屈服应力,并基于应力-应变关系,引入损伤比概念,对邓肯-张模型进行修正,建立了适用于强结构性黏土的邓肯-张修正模型。研究得出主要结论如下:
(1)昭通地区的天然沉积黏土具有极强的结构性,结构屈服应力高达800 kPa,e-lgp曲线在结构屈服应力前后由两条斜率不同的直线组成,原状土的Iv-lgp曲线显著高于ICL曲线。不同围压下的应力-应变关系曲线表现出明显的峰值,在应力大于结构屈服压力后强度大幅度减小。
(2)强结构性黏土的εl /(σ1−σ3) 随应变的变化规律可以划分为3个阶段,分别对应土体结构性完好、结构性逐渐破坏和结构性完全破坏3个阶段。
(3)在本文修正邓肯-张模型中,土体3个阶段的初始剪切模量有Ei1> Ei2 >Ei3的关系,各阶段的剪切模量随应变的增加而变化,与试验数据中强结构性土的剪切变形规律相符。利用本模型拟合的应力-应变关系与实际试验得出的应力-应变关系具有很高的拟合度,这表明修正后的邓肯-张模型能更好地适用于强结构性黏土。
本模型是基于常规三轴剪切试验得出的,因此该模型并未考虑土体体积应变的影响,考虑体积变形条件下土体的应力-应变关系是下一步研究的主要内容。
-
-
[1] 沈珠江. 结构性粘土的弹塑性损伤模型[J]. 岩土工程学报,1993,15(3):21-28. (SHEN Zhujiang. An eiasto-piastic damage model for cemented clays[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3): 21-28. (in Chinese) doi: 10.3321/j.issn:1000-4548.1993.03.003 [2] 谢定义, 齐吉琳. 土结构性及其定量化参数研究的新途径[J]. 岩土工程学报,1999,21(6):651-656. (XIE Dingyi, QI Jilin. Soil structure characteristics and new approach in research on its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 651-656. (in Chinese) doi: 10.3321/j.issn:1000-4548.1999.06.003 [3] 刘恩龙, 沈珠江. 结构性土强度准则探讨[J]. 工程力学,2007,24(2):50-55. (LIU Enlong, SHEN Zhujiang. Investagation on strength criterion for the structured soils[J]. Engineering Mechanics, 2007, 24(2): 50-55. (in Chinese) doi: 10.3969/j.issn.1000-4750.2007.02.009 [4] KAVVADAS M, AMOROSI A. A constitutive model for structured soils[J]. Géotechnique, 2000, 50(3): 263-273.
[5] 陶虎, 李雅娴, 陶洋, 等. 基于结构性参数的黄土边坡地质灾害定量评价[J]. 人民长江,2017,48(增刊1):211-214, 219. (TAO Hu, LI Yaxian, TAO Yang, et al. Quantitative evaluation of geological hazards of loess slope based on structural parameters[J]. Yangtze River, 2017, 48(Suppl1): 211-214, 219. (in Chinese) [6] 王立忠, 赵志远, 李玲玲. 考虑土体结构性的修正邓肯-张模型[J]. 水利学报,2004,35(1):83-89. (WANG Lizhong, ZHAO Zhiyuan, LI Lingling. Non-linear elastic model considering soil structural damage[J]. Journal of Hydraulic Engineering, 2004, 35(1): 83-89. (in Chinese) doi: 10.3321/j.issn:0559-9350.2004.01.016 [7] 陈昌禄, 邵生俊, 马林. 考虑黄土结构性的修正邓肯-张模型研究[J]. 西北农林科技大学学报(自然科学版),2011,39(11):223-228. (CHEN Changlu, SHAO Shengjun, MA Lin. Study on modified Duncan-Chang model considering loess structural[J]. Journal of Northwest A & F University (Natural Science Edition), 2011, 39(11): 223-228. (in Chinese) [8] 杨爱武, 梁超. 基于邓肯-张模型的结构性软土应力应变关系研究[J]. 水文地质工程地质,2014,41(4):75-79, 86. (YANG Aiwu, LIANG Chao. A study of the stress-strain relationship of structural soft soil based on the Duncan-Chang model[J]. Hydrogeology & Engineering Geology, 2014, 41(4): 75-79, 86. (in Chinese) [9] 谷建晓, 范理云, 吕海波, 等. 基于修正邓肯-张模型模拟红黏土应力-应变关系[J]. 桂林理工大学学报,2020,40(2):351-357. (GU Jianxiao, FAN Liyun, LÜ Haibo, et al. Simulation of the stress-strain curves of red clay based on modified Duncan-Chang model[J]. Journal of Guilin University of Technology, 2020, 40(2): 351-357. (in Chinese) doi: 10.3969/j.issn.1674-9057.2020.02.013 [10] 孙谷雨, 杨平, 刘贯荣. 南京地区冻结粉质黏土邓肯–张模型参数试验研究[J]. 岩石力学与工程学报,2014,33(增刊1):2989-2995. (SUN Guyu, YANG Ping, LIU Guanrong. Experimental test on constitutive relationship of Nanjing frozen silty clay considering Duncan-Chang model[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Suppl1): 2989-2995. (in Chinese) [11] 张琰, 张丙印, 李广信, 等. 压实黏土拉压组合三轴试验和扩展邓肯张模型[J]. 岩土工程学报,2010,32(7):999-1004. (ZHANG Yan, ZHANG Bingyin, LI Guangxin, et al. Combined tension-compression triaxial tests and extended Duncan-Chang model of compacted clay[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 999-1004. (in Chinese) [12] 龚晓南, 熊传祥, 项可祥, 等. 粘土结构性对其力学性质的影响及形成原因分析[J]. 水利学报,2000,31(10):43-47. (GONG Xiaonan, XIONG Chuanxiang, XIANG Kexiang, et al. The formation of clay structure and its influence on mechanical characteristics of clay[J]. Journal of Hydraulic Engineering, 2000, 31(10): 43-47. (in Chinese) doi: 10.3321/j.issn:0559-9350.2000.10.007 [13] 中华人民共和国交通运输部. 公路土工试验规程: JTG 3430—2020[S]. 北京: 人民交通出版社, 2020. Ministry of Transport of the People’s Republic of China. Test methods of soils for highway engineering: JTG 3430—2020[S]. Beijing: China Communications Press, 2020. (in Chinese)
[14] 中华人民共和国建设部. 岩土工程勘察规范: GB 50021—2001[S]. 北京: 中国建筑工业出版社, 2004. Ministry of Construction of the People’s Republic of China. Code for investigation of geotechnical engineering: GB 50021—2001[S]. Beijing: China Architecture & Building Press, 2004. (in Chinese)
[15] 李佩, 张春霞, 郭正堂, 等. 晚中新世-上新世中国西南昭通盆地粘土矿物学组合特征及南亚季风演化[C]∥2018年中国地球科学联合学术年会论文集. 北京: 中国和平出版社, 2018: 5-6. LI Pei, ZHANG Chunxia, GUO Zhengtang, et al. Characteristics of clay mineralogical assemblage and South Asian monsoon evolution in Zhaotong Basin, Southwest China from late Miocene to Pliocene[C]∥Proceedings of the 2018 China Joint academic Conference of Geosciences. Beijing: China Peace Publishing House, 2018: 5-6. (in Chinese)
[16] 洪振舜, 立石义孝, 邓永锋. 强结构性天然沉积土的强度变形特性[J]. 岩土力学,2004,25(8):1201-1204. (HONG Zhenshun, TATEISHI Yoshitaka, DENG Yongfeng. Mechanical behavior of a strongly-structured natural sedimentary soil[J]. Rock and Soil Mechanics, 2004, 25(8): 1201-1204. (in Chinese) doi: 10.3969/j.issn.1000-7598.2004.08.005 [17] BURLAND J B. On the compressibility and shear strength of natural clays[J]. Géotechnique, 1990, 40(3): 329-378.
[18] DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(5): 1629-1653. doi: 10.1061/JSFEAQ.0001458
[19] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004. LI Guangxin. Advanced soil mechanics[M]. Beijing: Tsinghua University Press, 2004. (in Chinese)
[20] 张诚厚. 两种结构性粘土的土工特性[J]. 水利水运科学研究,1983(4):68-74. (ZHANG Chenghou. Geotechnical properties of two kinds of structural clay[J]. Journal of Nanjing Hydraulic Research Institute, 1983(4): 68-74. (in Chinese) [21] LEROUEIL S, VAUGHAN P R. The general and congruent effects of structure in natural soils and weak rocks[J]. Géotechnique, 1990, 40(3): 467-488.
-
期刊类型引用(3)
1. 邱恩喜,潘宏宇,何巧玲,孙希望,万旭升,张蕊,王知深. 冻融条件下冰碛土力学特性试验及模型研究. 工程地质学报. 2024(03): 772-784 .  百度学术
百度学术
2. 李顺. 基于修正邓肯-张模型的沥青混凝土坝体应力变形分析. 江苏工程职业技术学院学报. 2024(02): 6-14 .  百度学术
百度学术
3. 丁旭升,张凌凯,樊培培. 不同排水方式的湿陷性黄土力学特性试验及邓肯-张模型的改进. 水利水电科技进展. 2024(06): 20-26+40 .  百度学术
百度学术
其他类型引用(6)



 Email Alerts
Email Alerts RSS
RSS
 下载:
下载: