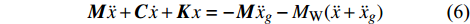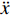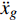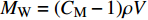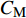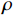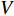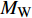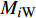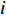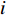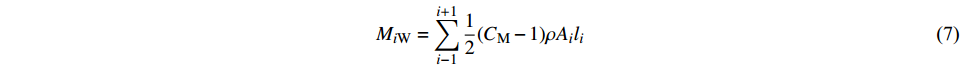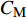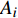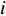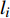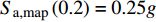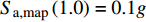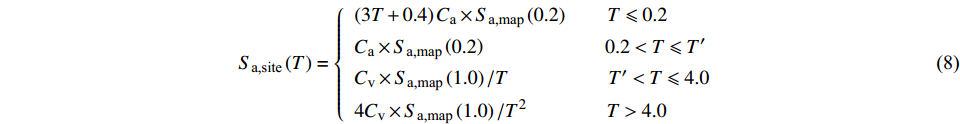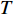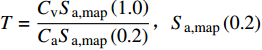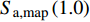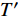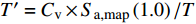Seismic fragility of offshore wind turbine considering scour depth
-
摘要: 在地震和波浪等复杂环境荷载作用下,海上风机的桩周冲刷和地震动水压力会显著影响海上风机的动力响应。建立了考虑地震动水压力及桩周冲刷效应的海上风机非线性动力计算模型,首先基于场地相关反应谱选取了34条地震动记录,通过多条带分析方法获取了不同工况下海上风机的地震易损性曲线,进一步讨论了地震动水压力和冲刷深度对海上风机地震易损性的影响。研究表明:在一般设防烈度下,冲刷深度对海上风机受到地震荷载作用时能否正常工作有显著影响,对风机发生永久性破坏概率的影响较小;而动水压力对海上风机4种极限状态下的地震易损性的影响均较小。海上风机易损性分析可为海上风机的抗震设计提供一定的理论指导,并具工程应用价值。Abstract: The geological conditions in the eastern coastal areas of China are complex, and the saturated soft clay around the offshore wind turbine foundation may be affected by the local erosion and dynamic water pressure conditions around the pile under the cyclic action of earthquake and waves. In this study, a nonlinear dynamic model of offshore wind turbine considering earthquake hydraulic pressure and scour effects was established. A total of 34 earthquake records were selected based on the site target response spectrum. Based on the multi-band analysis method, the seismic vulnerability curves of offshore wind turbine under various working conditions were obtained, and the influence of earthquake hydro-dynamic pressure and scour depth on the seismic vulnerability of offshore wind turbines was discussed further. The results indicate that under the seismic fortification intensity, the scour depth has a significant impact on the normal operation of offshore wind turbine under seismic load, but has marginal effect on the permanent failure of wind turbine. By comparison, the hydrodynamic pressure has little effect on the seismic vulnerability under different limit states. The vulnerability analysis of offshore wind turbine can serve as a guidance for the seismic design of offshore wind turbine.
-
Keywords:
- scour /
- hydrodynamic pressure /
- pile foundation /
- seismic fragility /
- offshore wind turbine
-
我国海上风力发电逐步进入快速化发展、规模化开发的阶段,海上风电场多建设在我国沿海地区,而我国地处欧亚地震带和环太平洋地震带交汇处,地震活动频繁,在过去几十年间,渤海、黄海、东海和东南沿海区域的6级以上强震达50多次,最大震级可达7.5级[1]。目前海上风机发展的主要趋势为单机容量和机身的大型化,对风机的抗震性能提出了更高的要求。
地震易损性分析能够有效表征结构物在地震荷载作用下的安全裕度,已有大量学者针对桥梁[2-4]和建筑物[5-6]的地震易损性展开了研究,而有关海上风机的地震易损性研究较少。Nuta[7]基于IDA法建立了加拿大地区风机钢塔架结构的地震易损性曲线;Patil等[8]针对1.65 MW的风机塔架结构进行了地震易损性分析,研究表明地基倾覆极限状态最为关键且近场地震更容易引起风机的破坏。苑晨阳[9]基于MSA法对停机状态下和正常运行状态下的风机进行了地震易损性分析,结果表明风机在停机状态下遭遇地震时更容易发生破坏。以上研究均假设风机塔筒底部直接固定在地面上,忽略了风机基础与土体的相互作用。De Risi等[10]采用非线性Winkler地基梁模型、阻抗函数和固定约束分别模拟海上风机的桩-土相互作用,研究表明采用阻抗函数或固定约束考虑桩-土相互作用时会低估风机在地震作用下的破坏概率。Kim等[11]采用非线性Winkler地基梁模型对海上风机进行地震易损性分析,指出仅采用弹簧较难模拟地震荷载作用下桩-土之间复杂的动力相互作用。
综上所述,现有的海上风机地震易损性研究中大多对风机基础进行了简化,未能精确模拟风机基础与海床的动力相互作用。近年来,冲刷对海上风机动力响应的影响引起了国内外众多学者的广泛关注,如刘红军等[12-13]研究表明冲刷深度会显著增加风机的动力响应,冲刷深度对海上风机地震易损性的影响仍需进一步研究。此外,根据Mo等[14]的研究,动水压力对风机地震易损性的影响也不可忽视。
本文以江苏响水沿海某风电场的1.5 MW风机结构为依托[15],建立了考虑地震和冲刷联合作用的海上风机模型,讨论冲刷深度及动水压力对海上风机地震易损性的影响。
1. 基于MSA的地震易损性分析
地震易损性分析是一种基于概率的结构抗震性能评估方法。易损性曲线表示在对应地震动强度指标(
$ {I}_{\mathrm{M}} $ )下结构破坏或达到某一极限状态的概率,一般采用地震动峰值速度(Peak Ground Velocity,PGV)、地震动峰值加速度(Peak Ground Acceleration,PGA)和对应结构基本周期的谱加速度(Sa)作为指标。根据所选的强度指标,假设在对应$ {I}_{\mathrm{M}} $ 下结构破坏的概率服从对数正态分布[16],即$ \mathrm{l}\mathrm{n}(x/\theta )/\beta\sim\mathrm{N}\left(\mathrm{0,1}\right) $ ,结构易损性方程表示为:$$ {p_{\text{f}}}\left( {{I_{\text{M}}} = x} \right) = \varPhi \left( {\frac{{\ln\dfrac{x}{\theta}}}{\beta }} \right)$$ (1) 式中:
$ {p}_{\mathrm{f}}({I}_{\mathrm{M}}=x) $ 为某地震波的地震动强度指标$ {I}_{\mathrm{M}}=x $ 时结构发生破坏的概率;$ \varPhi \left(\right) $ 为标准正态分布的累计分布函数;$ \theta $ 为易损性方程的中值,即破坏概率为50%时地震动强度指标$ {I}_{\mathrm{M}} $ 的值;$\; \beta $ 为$ \mathrm{l}\mathrm{n}{I}_{\mathrm{M}} $ 的标准差。在多条带分析法(Multiple Stripe Analysis)中,易损性方程参数估计是在离散的
$ {I}_{\mathrm{M}} $ 值下获取的,对应每一个$ {I}_{\mathrm{M}} $ 值会输入一系列不同的地震波进行结构分析,统计得到该$ {I}_{\mathrm{M}} $ 值水平下输入地震波导致结构破坏或超过某一设定极限状态的地震波数量,并假设每条地震波导致结构破坏或超过某一设定极限状态的概率是相互独立的。因此,可以假设在$ {I}_{\mathrm{M}}={x}_{j} $ 时输入$ {n}_{j} $ 条地震波,其中$ {z}_{j} $ 条地震波导致结构破坏或超过某一极限状态的概率服从二项分布,可表示为:$$ {P_j} = \left( {\begin{array}{*{20}{c}} {{n_{_j}}} \\ {{{\textit{z}}_j}} \end{array}} \right){p_j}^{{{\textit{z}}_j}}{\left( {1 - {p_j}} \right)^{{n_j} - {{\textit{z}}_j}}} $$ (2) 式中:
$ {p}_{j} $ 为$ {I}_{\mathrm{M}}={x}_{j} $ 时某一条地震波导致结构发生破坏的概率,即易损性方程(1)。根据结构分析的计算结果,采用最大似然估计法估计易损性方程的参数$ \theta 、\beta $ ,进一步得到使结构发生最大破坏概率的易损性方程,似然函数表示为:$$ L\left( {\theta ,\beta } \right) = \prod\limits_{j = 1}^m {\left( {\begin{array}{*{20}{c}} {{n_j}} \\ {{{\textit{z}}_j}} \end{array}} \right)} {p_j}^{{{\textit{z}}_j}}{\left( {1 - {p_i}} \right)^{{n_j} - {{\textit{z}}_j}}} $$ (3) 代入式(1)可得:
$$ L\left( {\theta ,\beta } \right) = \prod\limits_{j = 1}^m {\left( {\begin{array}{*{20}{c}} {{n_j}} \\ {{{\textit{z}}_j}} \end{array}} \right)} \varPhi {\left( {\frac{{\ln \frac{x_j}{\theta}}}{\beta }} \right)^{{{\textit{z}}_j}}}{\left[ {1 - \varPhi \left( {\frac{{\ln\frac{x_j}{\theta}}}{\beta }} \right)} \right]^{{n_j} - {{\textit{z}}_j}}} $$ (4) 式中:m为地震动强度指标
$ {I}_{\mathrm{M}} $ 的数量;$ \displaystyle\prod $ 表示连乘,由于$ \mathrm{l}\mathrm{n}L(\theta ,\beta ) $ 与$ \mathrm{l}\mathrm{n}L(\theta ,\beta ) $ 有相同的最大值点,$ \theta 、\beta $ 的最大似然估计为:$$ \left\{ {\hat \theta ,\hat \beta } \right\}{\text{ = }}\mathop {{\text{arg max}}}\limits_{\theta ,\beta } \sum\limits_{j = 1}^m {\left\{ {\ln \left( {\begin{array}{*{20}{c}} {{n_j}} \\ {{{\textit{z}}_j}} \end{array}} \right) + {{\textit{z}}_j}\ln \left[ {\varPhi \left( {\frac{{\ln \frac{x_j}{\theta}}}{\beta }} \right)} \right]} \right.} \left. { + \left( {{n_j} - {{\textit{z}}_j}} \right)\ln \left[ {1 - \varPhi \left( {\frac{{\ln \frac{x_j}{\theta}}}{\beta }} \right)} \right]} \right\}$$ (5) 2. 海上风机数值模型与地震动选取
2.1 数值模型与动水压力计算
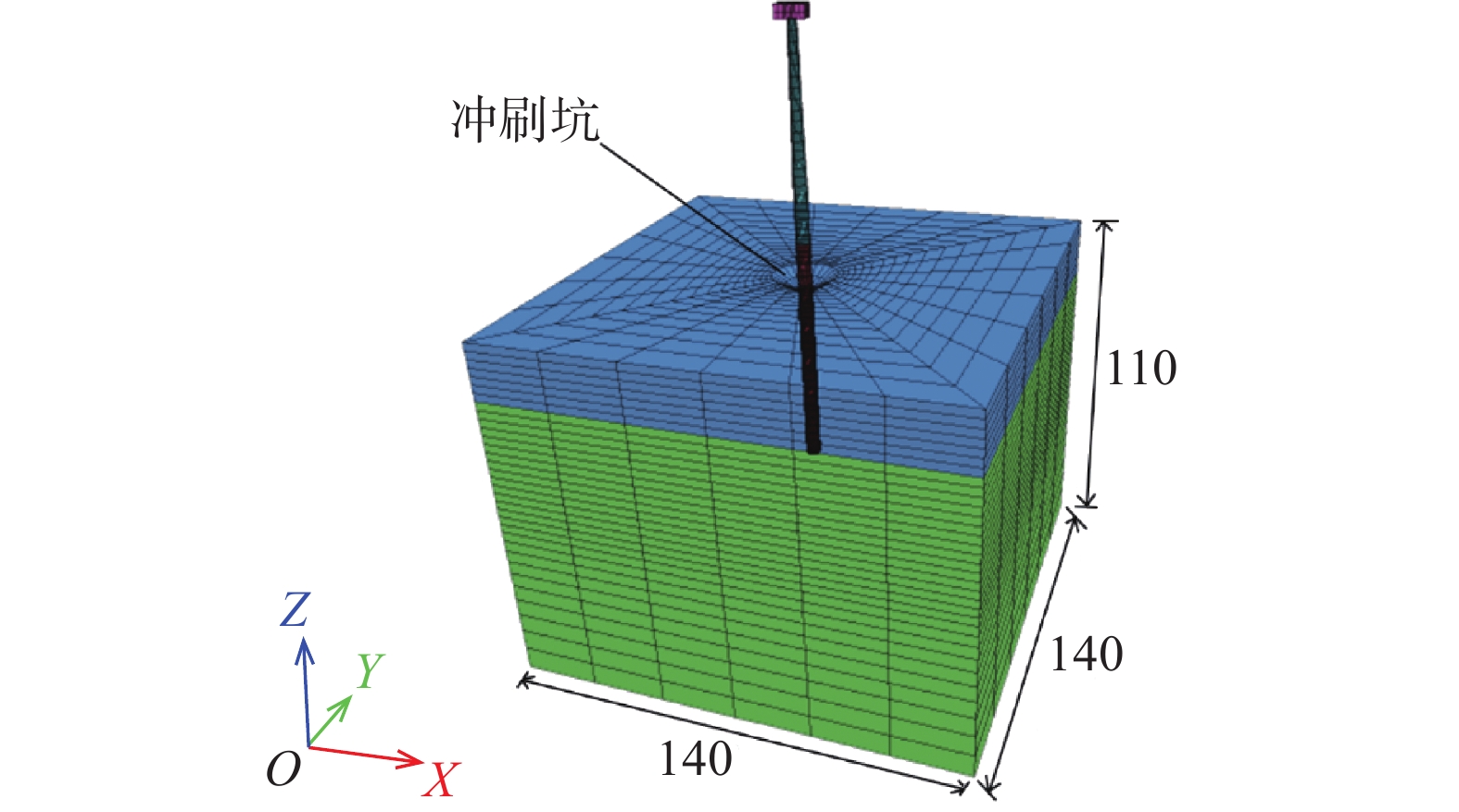
Patil等[8]研究表明,将机舱、轮毂和叶片整体进行简化对结构物前25阶模态的模态质量参与系数影响很小,可忽略不计。因此,将风机的数值模型简化为机舱、塔筒和桩基础3部分,其中将风机塔顶的机舱、轮毂和叶片整体简化为4 m×4 m×9 m的实体,通过质量等效方式将风机叶片和轮毂的质量附加在机舱的等效实体上;将塔筒简化为变截面的实心圆柱,分为上、中、下三段,详细参数见表1。 桩基础采用大直径钢管桩,桩径为4 m,壁厚0.045 m,桩总长70 m,入土深60 m,进入持力层深度为42 m,上覆软黏土18 m,桩与土层参数见表2。已有研究[17]表明在冲刷坑的尺寸参数中,冲刷深度的影响最大,而冲刷坑坡度通常为30°~44°[18],因此,本文将主要研究冲刷深度对海上风机地震动力响应的影响,取冲刷坑底部宽度为0,坡角取30°。为了同时满足计算精度和计算效率的需求,土体水平方向的长度取140 m,桩底以下持力层深度为50 m,土层总厚度为110 m,并对桩周网格进行加密,土体底部及边界的网格密度成比例递减。在模型底部输入地震波加速度时程曲线模拟地震荷载,采用附加质量法计算地震引起的动水压力。地震和冲刷联合作用海上风机数值模型如图1所示,模型单元数为13 536,节点数为14 645。机舱、塔筒和桩基础采用弹性本构,桩-土的接触面采用Coulomb摩擦模型。采用无质量地基地震动输入,在土体侧向施加自由场边界,底部直接施加应力时程。以瑞利阻尼叠加滞后阻尼模拟土体特性,瑞利阻尼参数为0.05和4.74,滞后阻尼使用sig4模型。
表 1 风机构件参数Table 1. Parameters of turbine序号 构件名称 尺寸 等效密度/(kg·m−3) 1 机舱 4 m×4 m×9 m 720 2 塔筒(上段) $ \varphi $ (3.4~2.6) m×30 m 180 3 塔筒(中段) $ \varphi $ (4.0~3.4) m×30 m 173 4 塔筒(下段) $ \varphi $ 4.0 m×10 m 264 表 2 数值模型的材料参数Table 2. Material parameters of numerical model材料名称 密度/
(kg·m−3)弹性模量/
kPa泊松比 黏聚力/
kPa内摩擦角/° Q345钢 7 850 2.06×108 0.27 − − 黏土 724 2.18×103 0.38 10 2.4 粉砂 1 130 8.00×104 0.33 0 22 在考虑动水压力时,结构物的动力平衡方程可表示为:
$$ {\boldsymbol{M}}\ddot{x}+{\boldsymbol{C}}\dot{x}+{\boldsymbol{K}}x=-{\boldsymbol{M}}{\ddot{x}}_{g}-{{{M}}}_{\mathrm{W}}(\ddot{x}+{\ddot{x}}_{g}) $$ (6) 式中:M、C、K分别为结构质量矩阵、阻尼矩阵、刚度矩阵;
$ \dot{x} $ 和$ \ddot{x} $ 分别为弹性运动速度和加速度;$ {\ddot{x}}_{g} $ 为刚性振动加速度;$ {M}_{\mathrm{W}}=({C}_{\mathrm{M}}-1)\rho V $ ,$ {C}_{\mathrm{M}} $ 为惯性力系数,$ \;\rho $ 为水的密度,$ V $ 为分析柱体的单位体积。由于模型在空间上为离散单元,可将动水压力的等效附加质量
$ {M}_{\mathrm{W}} $ 沿高度方向离散为$ {M}_{i\mathrm{W}} $ ,并作用在相应的结构物节点$ i $ 上,且假设相邻节点之间水与结构物的相对速度不变,即节点$ i $ 上的附加质量为相邻单元附加质量一半之和,即$$ {M}_{i\mathrm{W}}=\sum\limits _{i-1}^{i+1}\frac{1}{2}({C}_{\mathrm{M}}-1)\rho {A}_{i}{l}_{i} $$ (7) 式中:
$ {C}_{\mathrm{M}} $ 取2.0;$ {A}_{i} $ 为节点$ i $ 处的横截面积;$ {l}_{i} $ 为将结构物沿高度方向划分的单元长度。在海上风机的地震易损性研究中,其在地震作用下极限状态的定义尚未达到统一的标准。参考以往研究[7-8,10,14,19],并综合现有的海上风机地震易损性分析[7-12],本文中4种极限状态对应的临界响应值见表3,其中第四极限状态计算材料为Q345钢。
表 3 极限状态指标Table 3. Index of the limit state极限状态代号 极限状态标准 临界响应值 DS1 塔顶最大位移超过1.25% 塔身高度 0.925 m DS2 桩顶转角超过0.5° 0.5° DS3 震后塔顶最大位移超过1%塔身高度 0.74 m DS4 材料超过弹性极限对应的截面弯矩 158 MN·m 2.2 地震波选择与工况组合
由于场地条件、震级和震源等因素的不确定性,地震荷载是一种具有极大随机性的荷载形式。Elnashai等[20]指出选取地震波的震级波动范围应在0.6内且震源深度应在20~40 km;Hancock等[21]认为在进行结构地震动响应分析时,选取的地震波应与场地目标谱相匹配。本文根据DNV规范[22]和ISO 19901规范[23]中的规定,场地等级取E,并按ISO 19901规范中给出的重现期为1 000年的中国近海地震谱加速度地图,分别取
$ {S}_{\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{p}}\left(0.2\right)=0.25 g$ 和$ {S}_{\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{p}}\left(1.0\right)=0.1 g$ ,由式(8)计算近海软弱黏土场地条件的设计反应谱。$$ {S_{{\text{a,site}}}}\left( T \right) = \left\{ {\begin{array}{*{20}{l}} {\left( {3T + 0.4} \right){C_{\text{a}}} \times {S_{{\text{a,map}}}}\left( {0.2} \right)\qquad T \leqslant 0.2} \\ {{C_{\text{a}}} \times {S_{{\text{a,map}}}}\left( {0.2} \right)\qquad\qquad\qquad0.2 < T \leqslant {T'}} \\ {{C_{\text{v}}} \times {S_{{\text{a,map}}}}\left( {1.0} \right)/T\qquad\qquad\quad{T'} < T \leqslant 4.0} \\ {4{C_{\text{v}}} \times {S_{{\text{a,map}}}}\left( {1.0} \right)/{T^2}\qquad\qquad T > 4.0} \end{array}} \right. $$ (8) 式中:
$ T $ 为周期,可表示为$ T=\dfrac{{C}_{\mathrm{v}}{S}_{\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{p}}\left(1.0\right)}{{C}_{\mathrm{a}}{S}_{\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{p}}\left(0.2\right)},{S}_{\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{p}}\left(0.2\right) $ 和$ {S}_{\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{p}}\left(1.0\right) $ 分别表示振动周期为0.2 s和1.0 s时的地震加速度谱峰值,Ca和Cv为场地系数,根据场地等级 E 分别取1.0和1.8;$ {T}' $ 为临界周期,表示为${T}'={C}_{\mathrm{v}}\times {S}_{\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{p}}\left(1.0\right)/T$ 。为了模拟地震动的随机性,在进行地震易损性分析时需要选取大量的地震波,而现有研究表明在地震波数量达到32~36条时,基于MSA法的海上风机易损性分析即可达到一定精度[9]。因此,本文根据计算得到的设计反应谱,以及震源深度、震级波动范围,在太平洋地震工程研究中心(Peer)网站[24]上选取了34条地震记录,取比例因子为0.6,使得选取地震记录的平均加速度响应谱符合目标谱,对比结果如图2所示。
选取不同的水深和冲刷深度,讨论动水压力和冲刷深度对地震易损性的影响。选取2倍桩径为极限冲刷深度[12],3种工况组合如下:工况1的水深和局部冲刷深度Sd均为0;工况2的水深和局部冲刷深度Sd分别为10和0 m;工况2的水深和局部冲刷深度Sd分别为10和8 m。
3. 海上风机地震易损性分析
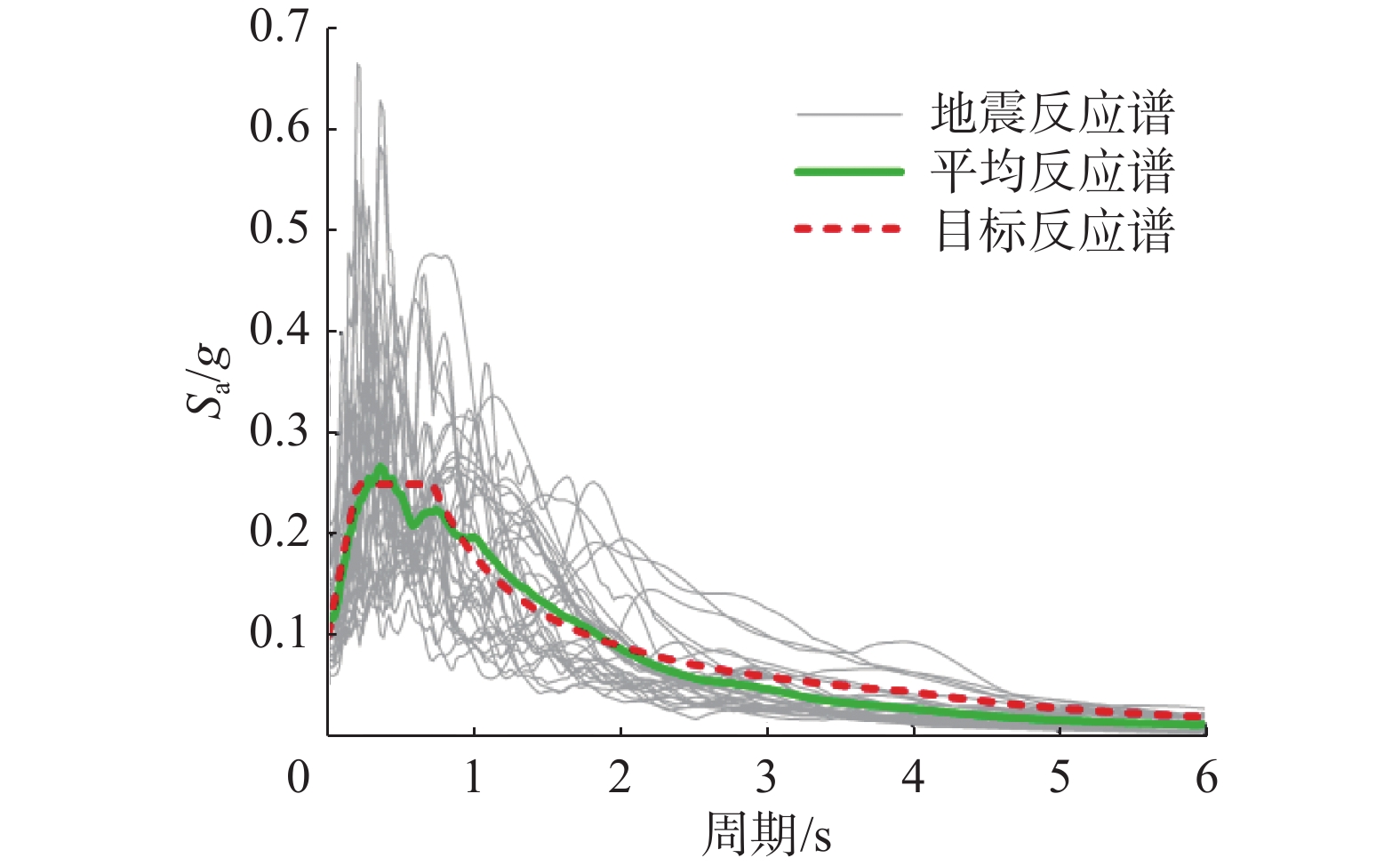
将选取的34条地震波分别调整其峰值加速度为0.2g、0.4g、0.6g、0.8g、1.0g和1.2g,在对应峰值加速度下分别计算不同工况的海上风机地震动响应,并记录对应的塔顶位移、桩顶转角、风机最大弯矩及震后累计位移,对比得到的目标响应和极限状态指标,并将分析结果代入式(5)。以第一强度指标为例,如图3所示为海上风机在不同峰值加速度幅值的不同地震波作用下的塔顶最大位移响应。其中红色虚线为DS1对应的塔顶位移,当塔顶位移超过红色虚线时,则风机达到第一极限状态,即发生“破坏”。易损性参数如表4所示。建立各极限状态指标下风机的地震易损性曲线,如图4所示。
表 4 海上风机地震易损性参数Table 4. Seismic vulnerability parameters of offshore wind turbine极限状态 工况 θ β 塔顶最大位移超过
1.25%塔身高度1 −0.59 0.72 2 −0.61 0.71 3 −0.90 0.69 桩顶转角超过0.5° 1 0.64 1.07 2 0.64 1.07 3 0.27 1.25 震后塔顶最大位移超过
1%塔身高度1 1.32 1.53 2 1.18 1.43 3 0.95 1.32 材料超过弹性极限
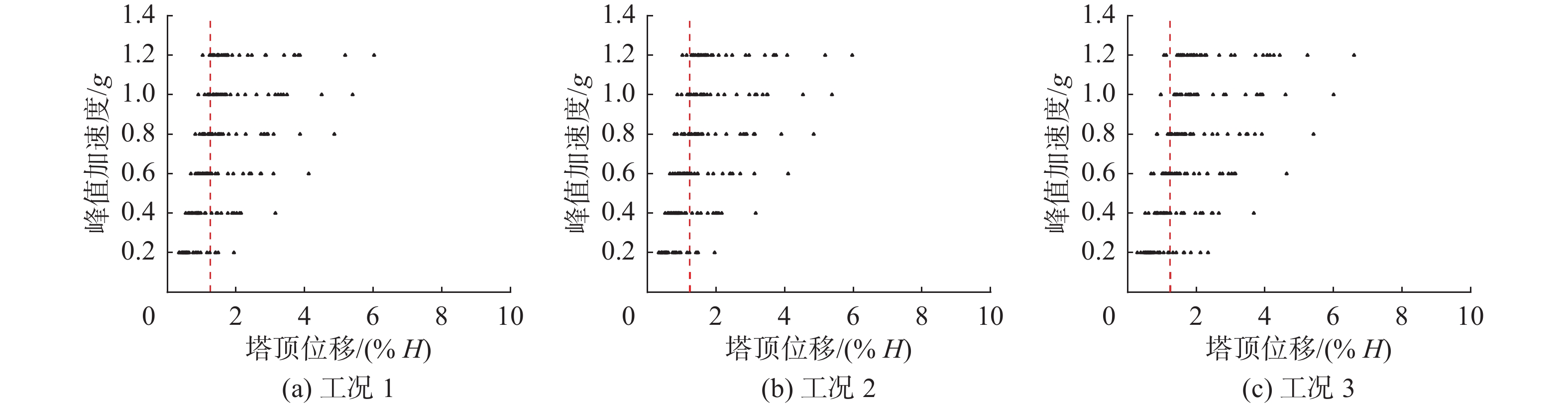
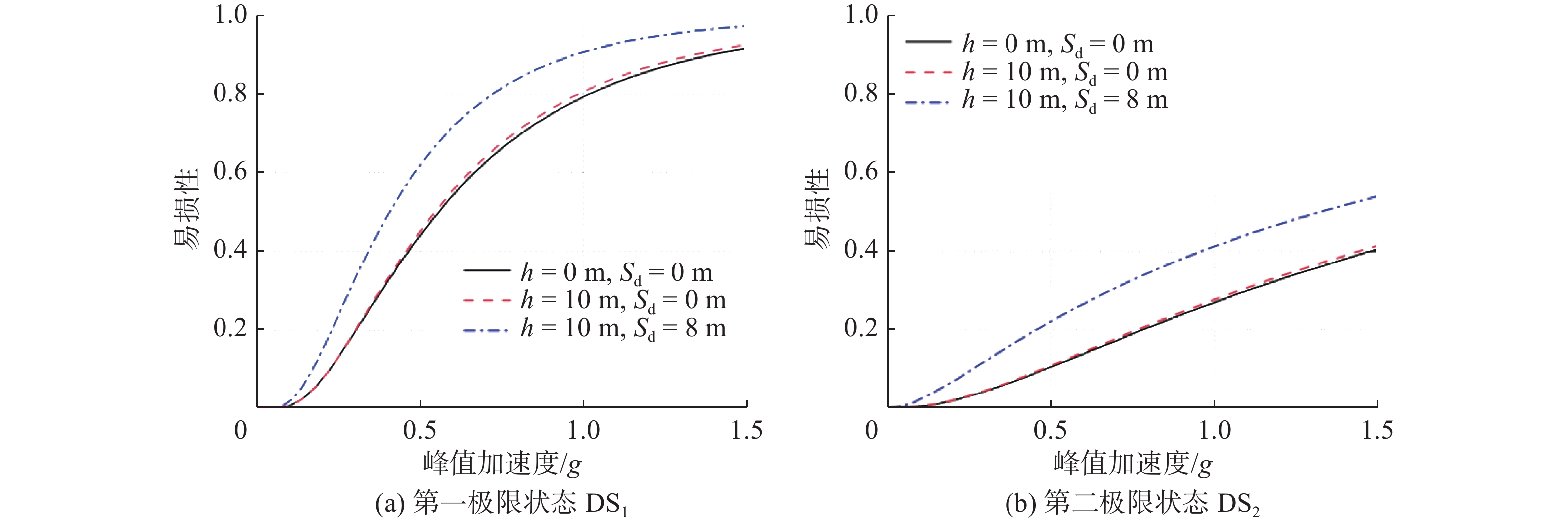
对应的截面弯矩1 1.76 1.12 2 1.10 0.65 3 1.43 1.14 以塔顶最大位移超过1.25% 的塔身高度为第一强度指标,由图4(a)可知在考虑冲刷深度影响时,海上风机的破坏概率显著增加,如PGA达到0.5g时,破坏概率达到了60%。根据ISO 19901-2规范[23]中对场地类别的划分,对3类和4类场地,即设防烈度为0.26g至0.45g的场地,考虑冲刷时,风机破坏概率的增幅超过了11%。然而动水压力对海上风机易损性的影响较小,如PGA小于0.4g时,风机破坏概率增幅仅0.7%;当PGA 达到0.8g时,风机破坏概率的增幅最大,达到1.41%。
以桩顶转角超过0.5°为破坏指标时,由图4(b)可知在PGA 达到1.0g时,冲刷深度对风机破坏概率影响最大,增幅达14.41%。对于3、4类的场地,即设防烈度为0.26g~0.45g时,风机破坏概率的增幅超过7%。然而随着PGA的增加,动水压力对风机破坏概率的影响逐渐增加,在PGA为1.5g时最大增幅为0.9%。
以震后塔顶最大位移超过1%塔身高度为极限状态指标时,图4(c)表明对于一般设防烈度的场地,即设防烈度小于0.5g时,考虑冲刷深度或动水压力对海上风机的易损性无明显影响。在PGA为1.5g时,同时考虑冲刷深度和动水压力影响使得风机的破坏概率增加了6.7%;仅考虑动水压力时,风机的破坏概率增加了0.08%。
以材料超过弹性极限对应的截面弯矩为极限状态指标时,由图4(d)可知考虑动水压力前后的易损性曲线几乎没有区别,这可能是由于风机达到第四极限状态时的概率太小,数值试验还无法反映出动水压力对地震易损性的影响。然而考虑冲刷深度时,随着PGA的增加风机破坏概率逐渐增加,当PGA小于0.5g时,冲刷深度对破坏概率的影响不显著,最大为1.42%;PGA大于1.5g时,最大增幅为 15.61%。
4. 结 语
本文建立了考虑地震动水压力及桩周冲刷效应的海上风机非线性动力计算模型,使用MSA法分析了冲刷深度和动水压力对海上风机地震易损性的影响,在本文提出的4个极限状态下,动水压力对海上风机地震易损性均无显著影响,但要注意以下2种情况:(1)风机不能正常工作时,即以塔顶最大位移超过1.25%塔身高度的第一极限状态和以桩顶转角超过0.5°的第二极限状态下,冲刷深度对风机易损性有显著影响,如在一般地震设防烈度下,即PGA小于0.5g时,冲刷深度引起风机破坏概率的增加非常显著,增幅达到17.85%和14.41%;(2)风机发生永久性损坏时,即以震后塔顶最大位移超过1%塔身高度的第三极限状态和以材料超过弹性极限对应的截面弯矩的第四极限状态下,冲刷深度对风机易损性有一定影响。在一般地震设防烈度下,冲刷深度的影响较小。对罕遇强地震,即当PGA达到1.0g以上时,冲刷深度对风机破坏概率的影响显著增加。
-
表 1 风机构件参数
Table 1 Parameters of turbine
序号 构件名称 尺寸 等效密度/(kg·m−3) 1 机舱 4 m×4 m×9 m 720 2 塔筒(上段) $ \varphi $ (3.4~2.6) m×30 m 180 3 塔筒(中段) $ \varphi $ (4.0~3.4) m×30 m 173 4 塔筒(下段) $ \varphi $ 4.0 m×10 m 264 表 2 数值模型的材料参数
Table 2 Material parameters of numerical model
材料名称 密度/
(kg·m−3)弹性模量/
kPa泊松比 黏聚力/
kPa内摩擦角/° Q345钢 7 850 2.06×108 0.27 − − 黏土 724 2.18×103 0.38 10 2.4 粉砂 1 130 8.00×104 0.33 0 22 表 3 极限状态指标
Table 3 Index of the limit state
极限状态代号 极限状态标准 临界响应值 DS1 塔顶最大位移超过1.25% 塔身高度 0.925 m DS2 桩顶转角超过0.5° 0.5° DS3 震后塔顶最大位移超过1%塔身高度 0.74 m DS4 材料超过弹性极限对应的截面弯矩 158 MN·m 表 4 海上风机地震易损性参数
Table 4 Seismic vulnerability parameters of offshore wind turbine
极限状态 工况 θ β 塔顶最大位移超过
1.25%塔身高度1 −0.59 0.72 2 −0.61 0.71 3 −0.90 0.69 桩顶转角超过0.5° 1 0.64 1.07 2 0.64 1.07 3 0.27 1.25 震后塔顶最大位移超过
1%塔身高度1 1.32 1.53 2 1.18 1.43 3 0.95 1.32 材料超过弹性极限
对应的截面弯矩1 1.76 1.12 2 1.10 0.65 3 1.43 1.14 -
[1] 彭艳菊, 孟小红, 吕悦军, 等. 我国近海地震活动特征及其与地球物理场的关系[J]. 地球物理学进展,2008,23(5):1377-1388 PENG Yanju, MENG Xiaohong, LÜ Yuejun, et al. The seismicity of China offshore seas and its relationship with geophysical fields[J]. Progress in Geophysics, 2008, 23(5): 1377-1388. (in Chinese)
[2] 庞于涛, 王建国, 欧阳辉, 等. 采用钢纤维混凝土的连续钢构桥地震易损性分析[J]. 哈尔滨工程大学学报,2018,39(4):687-694 PANG Yutao, WANG Jianguo, OUYANG Hui, et al. Seismic fragility analysis of a continuous rigid frame bridge made from steel fiber reinforced concrete[J]. Journal of Harbin Engineering University, 2018, 39(4): 687-694. (in Chinese)
[3] 陈伟, 王冠, 杜彦良, 等. 高速铁路连续梁桥近断层地震易损性分析[J]. 哈尔滨工程大学学报,2020,41(2):212-218 CHEN Wei, WANG Guan, DU Yanliang, et al. Vulnerability analysis of the continuous high-speed railway bridge under near-fault earthquake[J]. Journal of Harbin Engineering University, 2020, 41(2): 212-218. (in Chinese)
[4] 郭军军, 钟剑, 袁万城, 等. 考虑桥台性能影响的连续梁桥地震易损性分析[J]. 哈尔滨工程大学学报,2017,38(4):532-537 GUO Junjun, ZHONG Jian, YUAN Wancheng, et al. Seismic fragility analysis of a continuous bridge considering the performance of abutments[J]. Journal of Harbin Engineering University, 2017, 38(4): 532-537. (in Chinese)
[5] 冯云芬, 高树飞. 基于位移的高桩码头地震易损性分析[J]. 水利水运工程学报,2019(3):76-84 FENG Yunfen, GAO Shufei. Seismic vulnerability analysis of pile-supported wharves based on displacement[J]. Hydro-Science and Engineering, 2019(3): 76-84. (in Chinese)
[6] 王秀振, 钱永久, 邵长江, 等. 考虑楼层相关性的框架结构地震易损性分析[J]. 吉林大学学报(工学版),2020,50(1):202-209 WANG Xiuzhen, QIAN Yongjiu, SHAO Changjiang, et al. Seismic vulnerability analysis of frame structure considering floor correlation[J]. Journal of Jilin University (Engineering and Technology Edition), 2020, 50(1): 202-209. (in Chinese)
[7] NUTA E. Seismic analysis of steel wind turbine towers in the Canadian environment[D]. Toronto: University of Toronto, 2010.
[8] PATIL A, JUNG S, KWON O S. Structural performance of a parked wind turbine tower subjected to strong ground motions[J]. Engineering Structures, 2016, 120: 92-102. doi: 10.1016/j.engstruct.2016.04.020
[9] 苑晨阳. 大型风机结构振动的结构—机电智能控制研究[D]. 大连: 大连理工大学, 2017. YUAN Chenyang. Study on the structure-BCS intelligent control methods for mitigating the vibration of large-scale wind turbines[D]. Dalian: Dalian University of Technology, 2017. (in Chinese)
[10] DE RISI R, BHATTACHARYA S, GODA K. Seismic performance assessment of monopile-supported offshore wind turbines using unscaled natural earthquake records[J]. Soil Dynamics and Earthquake Engineering, 2018, 109: 154-172. doi: 10.1016/j.soildyn.2018.03.015
[11] KIM D H, LEE S G, LEE I K. Seismic fragility analysis of 5 MW offshore wind turbine[J]. Renewable Energy, 2014, 65: 250-256. doi: 10.1016/j.renene.2013.09.023
[12] 刘红军, 杨奇. 局部冲刷对风机支撑系统承载性能的影响[J]. 岩土力学,2018,39(2):722-727 LIU Hongjun, YANG Qi. Influence of local scour on bearing performance of wind turbine supporting system[J]. Rock and Soil Mechanics, 2018, 39(2): 722-727. (in Chinese)
[13] 宋波, 赵伟娜, 双妙. 冲刷深度对海上风电塔地震动力响应的影响分析[J]. 工程科学学报,2019,41(10):1351-1359 SONG Bo, ZHAO Weina, SHUANG Miao. Analysis of the influence of scour depth on the dynamic response of offshore wind turbine towers under earthquake action[J]. Chinese Journal of Engineering, 2019, 41(10): 1351-1359. (in Chinese)
[14] MO R J, KANG H G, LI M, et al. Seismic fragility analysis of monopile offshore wind turbines under different operational conditions[J]. Energies, 2017, 10(7): 1037. doi: 10.3390/en10071037
[15] 田树刚, 张爱军, 任文渊, 等. 基于流–固耦合的近海风电基础地震反应分析[J]. 岩石力学与工程学报,2015,34(1):155-165 TIAN Shugang, ZHANG Aijun, REN Wenyuan, et al. Analysis of seismic response of offshore structure of wind turbine and foundation considering fluid-structure coupling[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 155-165. (in Chinese)
[16] IBARRA L F, KRAWINKLER H. Global collapse of frame structures under seismic excitations[R]. Berkeley: Pacific Earthquake Engineering Research Center, 2005: 323-325.
[17] 林城, 韩杰, BENNETT C, 等. 冲刷作用下砂土地层中桩的侧向力学性质分析[J]. 南方能源建设,2018,5(2):24-36 LIN Cheng, HAN Jie, BENNETT C, et al. Analysis of laterally loaded piles in sand considering scour hole dimensions[J]. Southern Energy Construction, 2018, 5(2): 24-36. (in Chinese)
[18] RICHARDSON E V, DAVIS S R. Evaluating scour at bridges[R]. Washington, DC: Federal Highway Administration, 2001.
[19] ASAREH M A, SCHONBERG W, VOLZ J. Fragility analysis of a 5-MW NREL wind turbine considering aero-elastic and seismic interaction using finite element method[J]. Finite Elements in Analysis and Design, 2016, 120: 57-67. doi: 10.1016/j.finel.2016.06.006
[20] ELNASHAI A S, DI SARNO L. Fundamentals of earthquake engineering[M]. New York: Wiley & Sons, Ltd. , 2008: 365-367.
[21] HANCOCK J, BOMMER J J, STAFFORD P J. Numbers of scaled and matched accelerograms required for inelastic dynamic analyses[J]. Earthquake Engineering & Structural Dynamics, 2008, 37(14): 1585-1607.
[22] DET NORSKE VERITAS. Design of offshore wind turbine structures: DNV-OS-J101[S]. Oslo: Det Norske Veritas, 2010.
[23] ISO. Petroleum and natural gas industries-specific requirements for offshore structures—part 2: seismic design procedures and criteria: ISO 19901-2[S]. Switzerland: ISO, 2017.
[24] MAZZONI S. PEER ground motion database[DB/OL]. [2021-06-28]. https:∥ngawest2.berkeley.edu.
-
期刊类型引用(3)
1. 侯法垒,姚莫凡,胡雨承,张永,赵杨. 考虑外平台影响下海上风机单桩基础结构地震动力响应分析. 水力发电. 2024(01): 82-89+102 .  百度学术
百度学术
2. 郝文辉,李永进,吴宁宇,杨永焱,聂智超,曲树盛,张健. 基于AFL的海上风电单桩基础冲刷动力响应研究. 水道港口. 2024(01): 18-27 .  百度学术
百度学术
3. 李志川,祁雷,刘小燕,李宁,张庆巍,杜尊峰. 基于PC-Kriging模型的极端环境下海上风机基础可靠性分析. 船海工程. 2024(03): 84-89 .  百度学术
百度学术
其他类型引用(4)



 Email Alerts
Email Alerts RSS
RSS
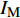
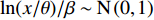
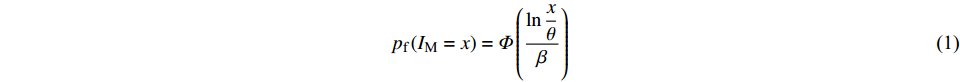
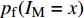
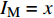
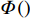
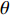

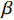
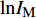
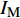
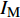
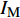
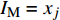
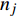
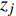
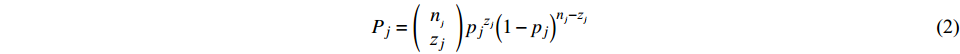
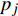
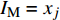
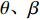
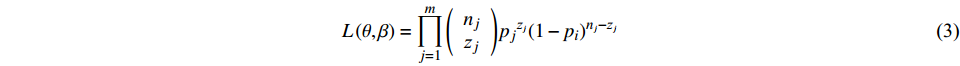
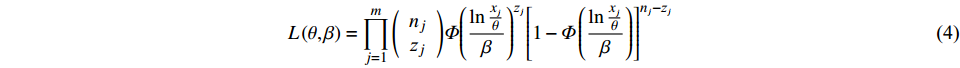
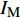

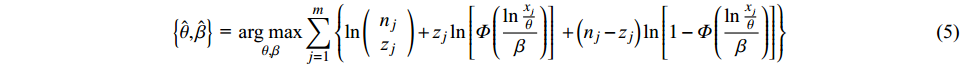
 下载:
下载: