Longitudinal analysis model of shield tunnel considering mechanical characteristics of ring joints
-
摘要: 盾构隧洞环间接头具有明显的非线性力学特性,合理模拟其受力变形响应是隧洞纵向变形分析中的难点。针对此问题提出了一种简便实用的环间接头分析模型,采用可传压不传拉的接触面单元模拟环间接触,采用基于埋置梁广义位移法的梁单元模拟螺栓,能够同时考虑环间接头处的非线性接触状态和接头螺栓的轴向刚度和剪切刚度,且适用于各种环间连接螺栓形状(直螺栓、弯螺栓或斜螺栓)。通过算例,将有限元模型与理论解析模型计算结果进行对比,验证了该模型的准确性。将该模型应用于某实际工程中穿越断层破碎带的盾构隧洞的纵向变形分析,结果表明:输水盾构隧洞在均质基岩中状态稳定,在断层破碎带区域衬砌环间缝变形和螺栓应力显著增大,但均在设计控制范围之内。该模型可为工程安全建设及运行提供一定参考。Abstract: The ring joints of shield tunnels have obvious nonlinear mechanical characteristics, and it is difficult to analyze the longitudinal deformation of tunnels reasonably to simulate the response of the stress and deformation. In order to solve this problem, this paper proposes a simple and practical model for the analysis of joints between rings, that is, the contact surface element that can transmit pressure but not tension is used to simulate the ring-to-ring contact, and the beam element based on the embedded beam generalized displacement method is used to simulate bolts. The nonlinear contact state at the joint between the rings and the axial stiffness and shear stiffness of the joint bolts are considered, and it is suitable for all kinds of bolt shapes between the rings (straight bolts, bent bolts or oblique bolts). A calculation example is used to compare the calculation results of the finite element and the theoretical analysis model to verify the accuracy of the model. The model is applied to the longitudinal deformation analysis of shield tunnels crossing the fault fracture zone in an actual project. The results show that the water conveyance shield tunnel is stable in homogeneous bedrock; and the deformation of the lining ring joints in the fault fracture zone and the bolt stress increase significantly, but are within the design control range. The model can provide a certain reference for engineering safety construction and operation.
-
随着我国盾构隧洞建设规模的不断扩大,在长距离隧洞修建过程中难免会遇到穿越断层破碎带等不良地质段,严重威胁隧洞的施工进度和安全运行[1-2]。在地层变形、荷载变化、地震等不利因素的影响下,盾构隧洞结构的薄弱部位环间接头处更易发生环缝张开、错台、螺栓屈服、管片裂损等问题[3-4]。目前关于盾构隧洞横断面的管片接头的研究成果较多,但是针对隧洞纵向变形环间接头的研究较少[5]。盾构隧洞纵向力学行为的研究方法主要有接头试验、理论解析和有限元数值分析3种。其中,衬砌足尺试验成本较大,国内此类研究较少[6]。理论解析方面,按不同的接头等效方法主要分为两种:一是以志波由紀夫等为代表的纵向等效连续化模型[7];二是以小泉淳等为代表的纵向梁-弹簧模型[8]。其中等效连续化模型应用最广泛,张文杰等[9-11]众多学者综合考虑横向刚度、环缝影响范围、螺栓弹塑性、橡胶衬垫等因素对该模型进行了修正改进。虽然理论解析法计算模型建模方便、计算简单,但过多的简化假定影响其准确性和可靠性[12],且难以用于环间接头不同螺栓连接情况的分析。有限元数值分析可以充分考虑土层和结构的属性,能够准确模拟衬砌、接头及隧洞-地基间的相互作用,故在研究隧洞纵向结构性能方面得到广泛应用。目前,环间接头模拟方法主要采用弹簧单元或者杆单元模拟环间连接螺栓。由于接头处承受轴力、剪力及弯矩的共同作用,所以采用弹簧单元模拟时需设定不同属性的弹簧单元,单元较多,布置复杂;且弹簧刚度主要依据经验取值,主观性大[13-14]。采用杆单元模拟螺栓时,只能考虑螺栓的轴向刚度,难以反映螺栓剪切刚度对抵抗环间接头变形的贡献。
基于此,本文提出可综合考虑环间接头非线性受力特性、接缝面传力特性及螺栓预紧力作用等因素影响的环间接头模拟方法,即采用非线性接触面单元模拟环间接缝面,采用基于埋置梁广义位移法的梁单元模拟螺栓,同时考虑螺栓的轴向刚度和剪切刚度,且适用于各种管片环间连接螺栓形状(直螺栓、弯螺栓或斜螺栓)。以某工程为依托,研究输水盾构隧洞穿越断层破碎带不良地质条件下的纵向变形,得出螺栓受力分布、环间接缝张开错台变形等环间接头受力和变形规律等,为穿越破碎带盾构隧洞工程设计和建设提供参考。
1. 环间接头模拟分析方法
隧洞纵向变形分析范围涉及几十甚至上百个衬砌环,计算模型复杂,计算量庞大,需要对接头作适当简化[15-16]。环间接头的模拟主要包括含衬垫和密封圈的接缝面及连接螺栓。采用可传压不传拉的接触单元模拟接缝面,采用埋置梁单元模拟连接螺栓。以此为基础建立一种能够准确反映环间接头非线性受力特性的纵向变形计算模型。
1.1 埋置梁广义位移法
将埋置于等参单元内的梁单元节点的广义位移求解方法简称为埋置梁广义位移法。当梁单元埋置于等参单元内时,假定与梁相连处等参单元节点位于梁内,根据旋度公式,可建立梁截面上角位移
$({\bar{\theta }}_{x},{\bar{\theta }}_{y},{\bar{\theta }}_{{\textit{z}}})$ 与线位移$(\bar{u},\bar{v},\bar{w})$ 之间的协调关系:$$ {\bar \theta _x} = \frac{1}{2}\left( { - \frac{{\partial \bar v}}{{\partial \bar {\textit{z}}}} + \frac{{\partial \bar w}}{{\partial \bar y}}} \right),{\bar \theta _y} = \frac{1}{2}\left( { - \frac{{\partial \bar w}}{{\partial \bar x}} + \frac{{\partial \bar u}}{{\partial \bar {\textit{z}}}}} \right),{\bar \theta _{\textit{z}}} = \frac{1}{2}\left( { - \frac{{\partial \bar u}}{{\partial \bar y}} + \frac{{\partial \bar v}}{{\partial \bar x}}} \right) $$ (1) 设埋置于等参单元的梁单元节点集合为:
$$ {\boldsymbol{D}} = \left\{ {{d_1}{\text{ }},{d_2}, \cdots ,{d_m}} \right\} $$ (2) 式中:m为节点总数。对其中任意节点
${d_i}$ 可找出包含该节点的所有等参单元E:$$ {\boldsymbol{E}} = \left\{ {{e_1}{\text{ }},{e_2}, \cdots ,{e_i}} \right\} $$ (3) 式中:
${e_i}$ 为包含该节点的等参单元总数。设$xy{\textit{z}}$ 为整体坐标系,与节点${d_i}$ 相连的梁单元的局部坐标系$\bar x\bar y\bar{\textit{z}}$ 中的$\bar x$ 为梁单元的轴向,$\bar y$ 和$\bar{\textit{z}}$ 根据梁单元的截面特性参数定义。设局部坐标与整体坐标之间的转换矩阵为R:$$ {\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{r_{\bar xx}}}&{{r_{\bar xy}}}&{{r_{\bar x{\textit{z}}}}} \\ {{r_{\bar yx}}}&{{r_{\bar yy}}}&{{r_{\bar y{\textit{z}}}}} \\ {{r_{\bar {\textit{z}}x}}}&{{r_{\bar {\textit{z}}y}}}&{{r_{\bar {\textit{z}}{\textit{z}}}}} \end{array}} \right] $$ (4) $$ \left\{ {\begin{array}{*{20}{c}} {\bar u } \\ {\bar v } \\ {\bar w } \end{array}} \right\} = {\boldsymbol{R}}\left\{ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right\} $$ (5) 对应于局部坐标和整体坐标系下的任一点位移分别为
${\bar {\boldsymbol{U}}} = {\left\{ {\bar u,\bar v,\bar w} \right\}^{\text{T}}}$ 和${\boldsymbol{U}} = {\left\{ {u,v,w} \right\}^{\text{T}}}$ 。设节点${d_i}$ 在任一等参单元${e_j}$ 中的局部坐标为${\left( {\xi {\text{,}}\eta {\text{,}}\zeta } \right)_{{e_j}}}$ ,根据等参单元的特点,节点${d_i}$ 由单元${e_j}$ 表示的平动位移${\bar {\boldsymbol{U}}} _{{d_i}}^{{e_j}}$ 可由单元${e_j}$ 的节点位移插值求得,即位移协调条件,其表达式为:$$ {\bar {\boldsymbol{U}}}_{{d_i}}^{{e_j}} = \sum\limits_{k = 1}^n {{N_k}(\xi ,\eta ,\zeta ) {{{\bar {\boldsymbol{U}}}_k}} } = {\boldsymbol{N}} _{{d_i}}{{\bar {\boldsymbol{U}}} _{{e_j}}} $$ (6) 式中:
$n$ 为单元${e_j}$ 的节点总数;N为单元形函数。节点
${d_i}$ 的转动位移可表示成单元${e_j}$ 的节点位移的线性组合形式,根据式(1)有:$$ {\bar {\boldsymbol{\theta}} } _{{d_i}}^{{e_j}} = \sum\limits_{k = 1}^n {{{{\boldsymbol{B}}}_k} {{{\bar {\boldsymbol{U}}}_k}} } = {{\boldsymbol{B}}_{{d_i}}}{ {\bar {\boldsymbol{U}}} _{{e_j}}} ,\;\;{{\boldsymbol{B}}_k} = \left[ {\begin{array}{*{20}{c}} 0&{ - \dfrac{1}{2}\dfrac{{\partial {N_k}}}{{\partial \bar {\textit{z}}}}}&{\dfrac{1}{2}\dfrac{{\partial {N_k}}}{{\partial \bar y}}} \\ {\dfrac{1}{2}\dfrac{{\partial {N_k}}}{{\partial \bar {\textit{z}}}}}&0&{ - \dfrac{1}{2}\dfrac{{\partial {N_k}}}{{\partial \bar x}}} \\ { - \dfrac{1}{2}\dfrac{{\partial {N_k}}}{{\partial \bar y}}}&{\dfrac{1}{2}\dfrac{{\partial {N_k}}}{{\partial \bar x}}}&0 \end{array}} \right] $$ (7) 节点的平均平动位移和平均角位移为:
$$ { {\bar U} _{{d_i}}} = \frac{1}{{{e_i}}}\sum\limits_{{e_j} = 1}^{{e_i}} { {\bar U} _{{d_i}}^{{e_j}}}, \;\;{ {\bar \theta } _{{d_i}}} = \frac{1}{{{e_i}}}\sum\limits_{{e_j} = 1}^{{e_i}} { {\bar \theta } _{{d_i}}^{{e_j}}} $$ (8) 对整个系统求解时,必须在整体坐标系下进行,故上述两式可转换成整体坐标下埋置于等参单元内的梁单元节点广义位移表达式:
$$ \begin{split} {\left\{ {\begin{array}{*{20}{c}} {\boldsymbol{U}} \\ {\boldsymbol{\theta}} \end{array}} \right\}_{{d_i}}} = &{\left[ {\begin{array}{*{20}{c}} {\boldsymbol{R}}&0 \\ 0&{\boldsymbol{R}} \end{array}} \right]^{\text{T}}}{\left\{ {\begin{array}{*{20}{c}} {\bar {\boldsymbol{U}}} \\ {\bar {\boldsymbol{\theta}} } \end{array}} \right\}_{{d_i}}} = {\left[ {\begin{array}{*{20}{c}} {\boldsymbol{ R}}&0 \\ 0&{\boldsymbol{R }} \end{array}} \right]^{\text{T}}}\frac{1}{{{e_i}}}\sum\limits_{{e_j} = 1}^{{e_i}} {\left\{ {\begin{array}{*{20}{c}} {\bar {\boldsymbol{U}}} \\ {\bar {\boldsymbol{\theta}} } \end{array}} \right\}_{{d_i}}^{{e_j}}} = \frac{1}{{{e_i}}}\sum\limits_{{e_j} = 1}^{{e_i}} {{{\left[ {\begin{array}{*{20}{c}} {\boldsymbol{R}}&0 \\ 0&{\boldsymbol{R}} \end{array}} \right]}^{\text{T}}}{{\left[ {\begin{array}{*{20}{c}} {\boldsymbol{N}} \\ {\boldsymbol{B}} \end{array}} \right]}_{{d_i}}}{{ {\bar U} }_{{e_j}}}} =\\& \frac{1}{{{e_i}}}\sum\limits_{{e_j} = 1}^{{e_i}} {{{\left[ {\begin{array}{*{20}{c}} {\boldsymbol{R}}&0 \\ 0&{\boldsymbol{R}} \end{array}} \right]}^{\text{T}}}{{\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{I}}{{\boldsymbol{N}}_1}}&{{\boldsymbol{I}}{{\boldsymbol{N}}_2}}& \cdots &{{\boldsymbol{I}}{{\boldsymbol{N}}_n}} \\ {{{\boldsymbol{B}}_1}}&{{{\boldsymbol{B}}_2}}& \cdots &{{{\boldsymbol{B}}_n}} \end{array}} \right]}_{{d_i}}}} \left[ {\begin{array}{*{20}{c}} {\boldsymbol{R}}&0& \cdots &0 \\ 0&{\boldsymbol{R}}& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{\boldsymbol{R}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_1}} \\ {{{\boldsymbol{U}}_2}} \\ \vdots \\ {{{\boldsymbol{U}}_n}} \end{array}} \right]_{{e_{\text{j}}}}} \end{split} $$ (9) 式中: I为单位矩阵。
1.2 接触模拟方法
盾构隧洞衬砌环间接缝面需要考虑接触,按传压不传拉模拟,采用8节点Goodman接触单元[17]。此接触单元在本构关系上同时考虑了接触面法向和切向的非线性特性,能够较好地模拟接触面闭合、滑移和张开等不同的接触状态,使计算结果更符合实际情况。
计算中根据法向正应力判断接触单元处于何种状态,规定了接触面的3种变形模式:(1)法向应力
${\sigma _{\text{n}}}$ ≤0,切向应力$\tau $ <S,此时认为接触单元处于闭合模式;(2)法向应力${\sigma _{\text{n}}}$ ≤0,切向应力$\tau $ ≥S,此时认为接触单元处于滑移模式;(3)法向应力${\sigma _{\text{n}}}$ >0(或大于抗拉强度),认为接触单元处于张开模式,此时法向、切向刚度均取接近0的小值。其中:${\sigma _{\text{n}}}$ 受压为负,受拉为正;$\tau $ 为单元切向剪应力,S为根据摩尔-库仑准则计算的抗剪强度。接触计算是典型的非线性问题,接触面处于张开模式时无法承担的应力,以及接触面处于滑移模式时大于抗剪强度的部分应力会在每一次荷载增量的迭代过程中重新分配到周围单元中去。计算时需要将荷载细分,分增量步施加,将上一增量步的接缝面接触应力和接触状态作为当前增量步的初始值,接触问题非线性迭代采用变刚度法,直至前后两次的迭代结果相近再进入下一计算步。
2. 算例验证和讨论
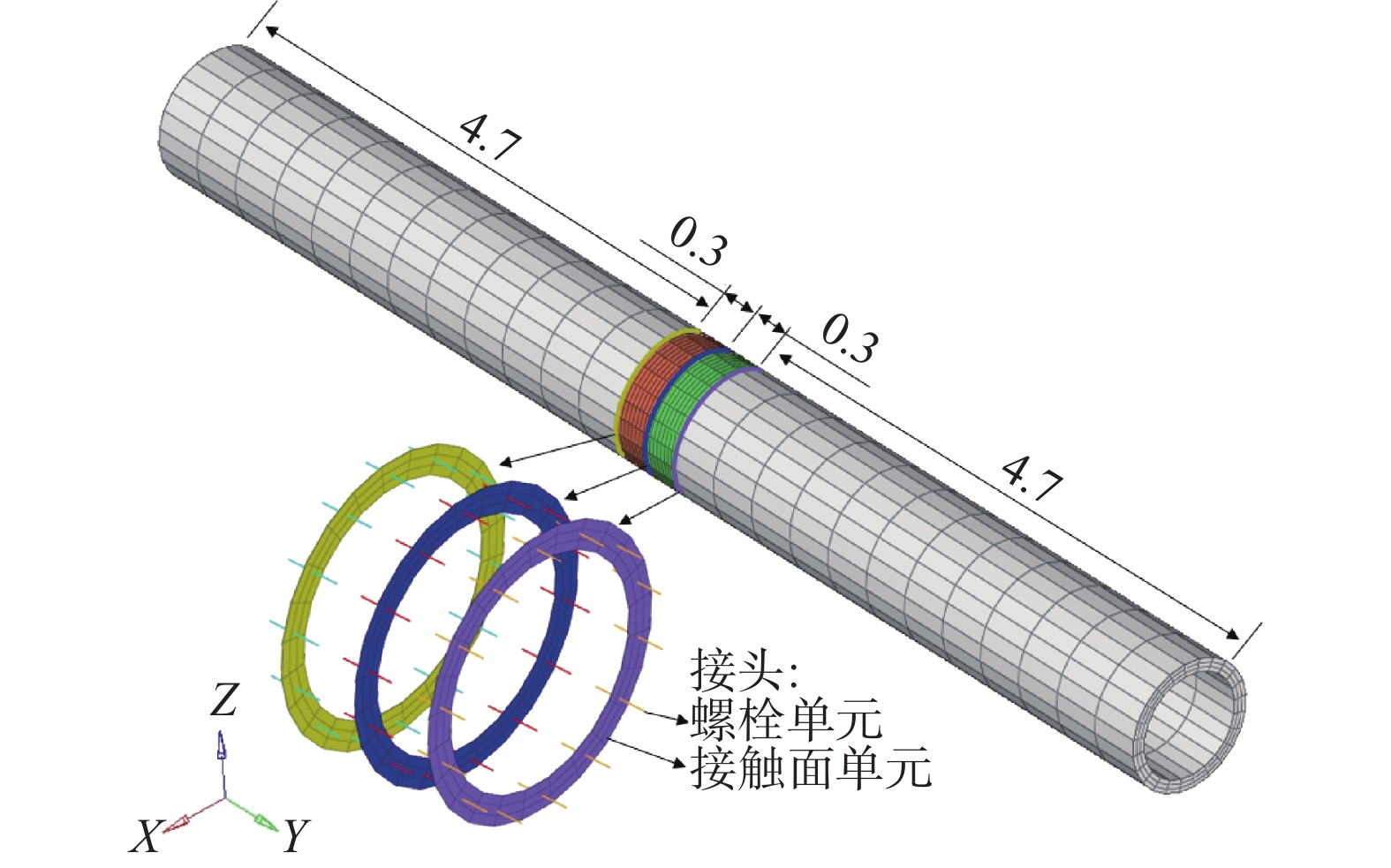
本文选取以中部带有环间接头的混凝土悬臂梁受均布荷载作用下的受力响应为例,论证所提出方法的正确性。如图1所示,梁的横截面与盾构隧洞衬砌相似,为圆环形,外径1.0 m,内径0.8 m,长度10 m,弹性模量3×104 MPa,泊松比0.2。悬臂梁结构由首尾的2个长环段和中部的2个短环段通过接头连接而成,长环段长4.7 m,短环段长0.3 m,接头处由14根M30直螺栓连接,螺栓沿环向均匀分布。螺栓长度0.2 m,弹性模量200 GPa,性能等级8.8级,屈服强度640 MPa。悬臂梁结构上表面作用有竖直向下的均布荷载q=1×105 N/m2,作用范围为10 m(长)×1 m(宽),梁结构左端固定约束。
悬臂梁采用等参单元进行离散,螺栓采用基于埋置梁广义位移法的梁单元进行模拟,接头处设置上文所述的非线性接触单元,按传压不传拉模拟。有限元模型如图2所示。为验证螺栓梁单元可承担剪力,此算例中考虑该接触面不承担剪力,接头处剪力由螺栓承担。接触面单元的切向刚度取为接近0的小值,初始法向刚度取3×1012 N/m3。
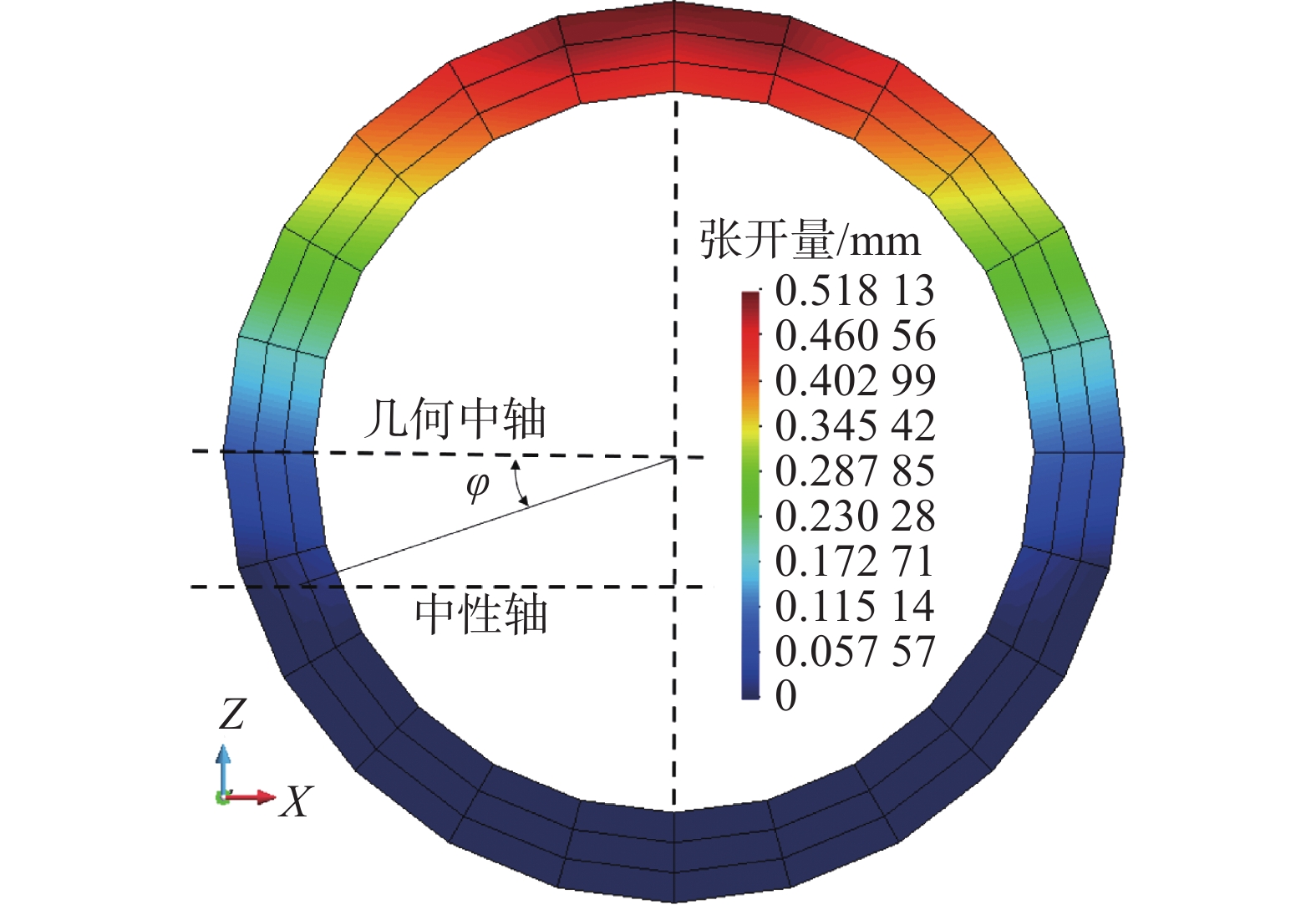
悬臂梁变形如图3所示,以两短环段之间的环间接头为研究对象,可以看出在接头处出现了明显的张开错动变形。接触面处的张开量分布如图4所示,可知接头处拱顶及拱腰位置普遍张开,为受拉区,最大张开值为0.52 mm,发生在截面顶部。拱底位置未张开,为受压区,中性轴位置角度约为22°。接头处连接螺栓轴力分布见图5,可知在中性轴以上的受拉区螺栓拉力增大,最大拉力为335.90 kN,最大拉应力为475.20 MPa,发生在顶部螺栓处。中性轴以下位置螺栓轴力几乎为0,这表明在受压区由混凝土承压,螺栓不受轴力作用。
在结构整体无轴向拉力作用情况下,环缝张开由弯矩作用产生。均布荷载下悬臂梁中点处弯矩理论值为1 250 kN∙m,根据文献[5]中纯弯状态下环间接头理论解析模型可求得中性轴位置、环间最大张开量及螺栓最大拉应力(见表1)。
表 1 有限元法和解析法计算结果Table 1. Calculation results of finite element method and analytical method分类 中性轴
位置/°环间最大
张开量/mm螺栓最大
拉应力/MPa有限元数值解 约22 0.52 475.20 理论解析解 23.93 0.51 470.14 对比有限元法和解析法计算结果,可知环间最大张开量及螺栓最大拉力均相近,验证了本文所提出的环间接头模拟方法的正确性。其略有差异的主要原因是理论分析模型中假定了螺栓为环向连续均匀分布。
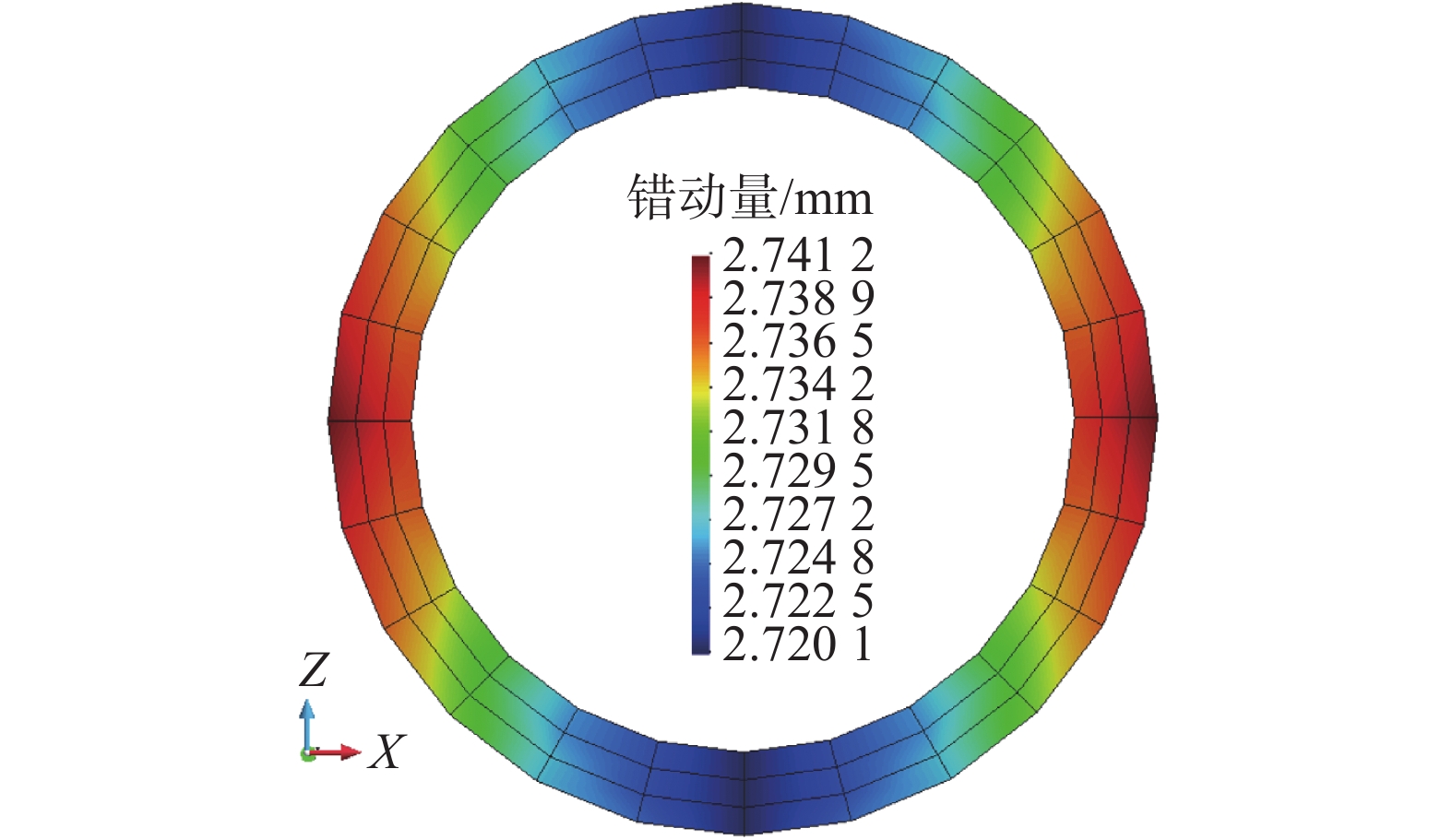
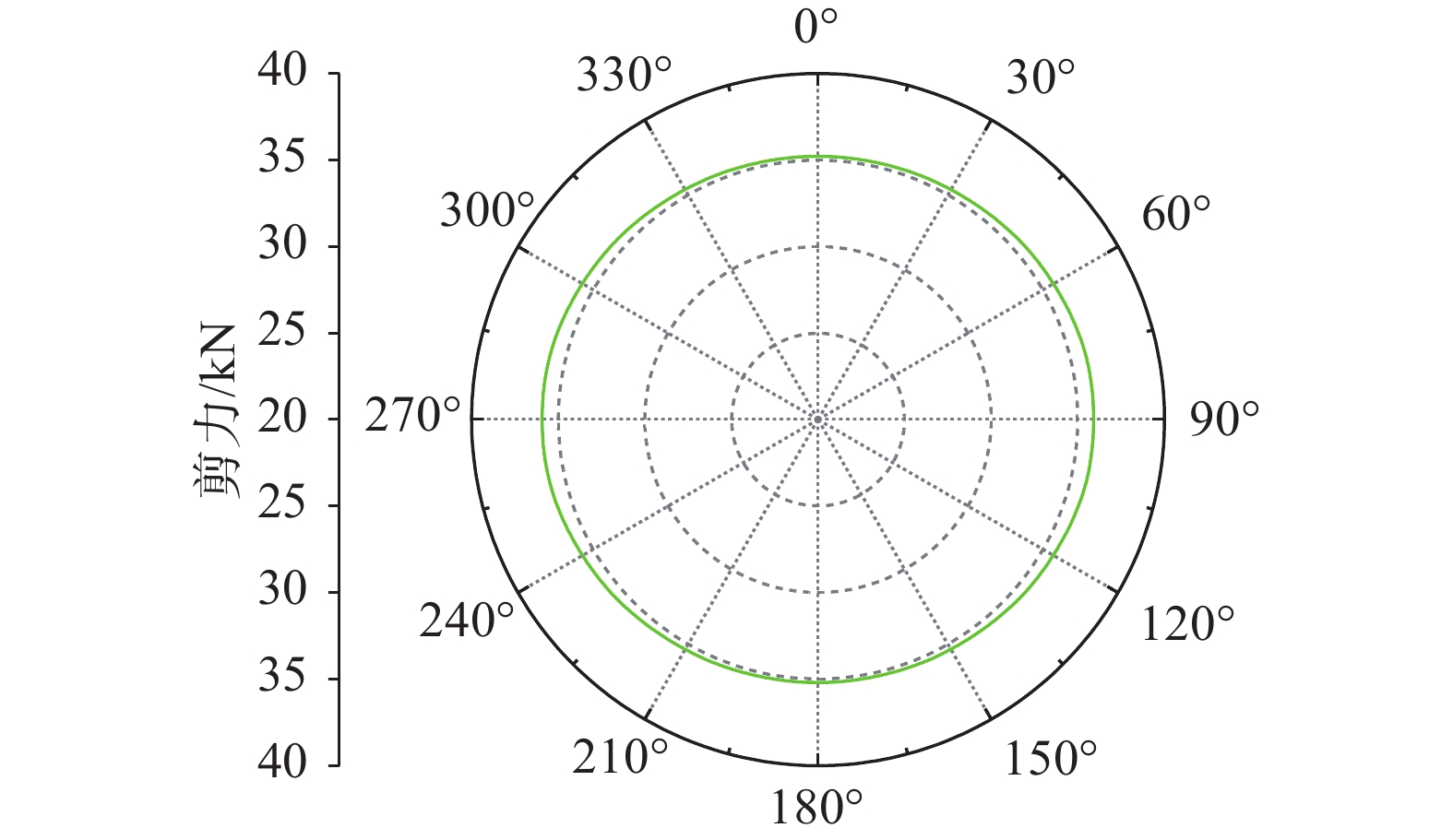
接触面处的错动量分布如图6所示,可知环间错动量均在2.70 mm左右,最大相差未超过1%。螺栓剪力分布如图7所示,可知14根螺栓剪力几乎一致,均在35.50 kN左右,最大相差未超过1%。
均布荷载下悬臂梁中点处剪力理论值500 kN,由于该算例中考虑接触面不抗剪,剪力由14根螺栓均匀分担,每个螺栓承担剪力理论值为35.71 kN,与有限元计算结果相符。
由此可见,在受拉区,接触面张开,由螺栓承担拉力,环间最大张开值及螺栓最大拉力值与理论值相符;在受压区,压力由混凝土承担,螺栓轴力几乎为0;接头处截面错动及每个螺栓承担的剪力大小几乎一致,且与理论值相符。
在实际工程应用中,接头处受力复杂,同时还有螺栓预紧力作用,且连接螺栓型式多样,现有解析模型基本都采用直螺栓进行推导,不同连接螺栓型式条件下解析模型可能不再适用。因此,采用本文提出的方法构建接头模型,不受螺栓型式限制,预紧力便于模拟,既可体现在荷载作用下接头处的张开错动变形,又可获得螺栓的受力分布。此方法考虑了螺栓抗拉和抗剪能力,同时还考虑了接头处接触非线性问题,可以很好地模拟接头的力学行为和非线性状态。
3. 工程应用
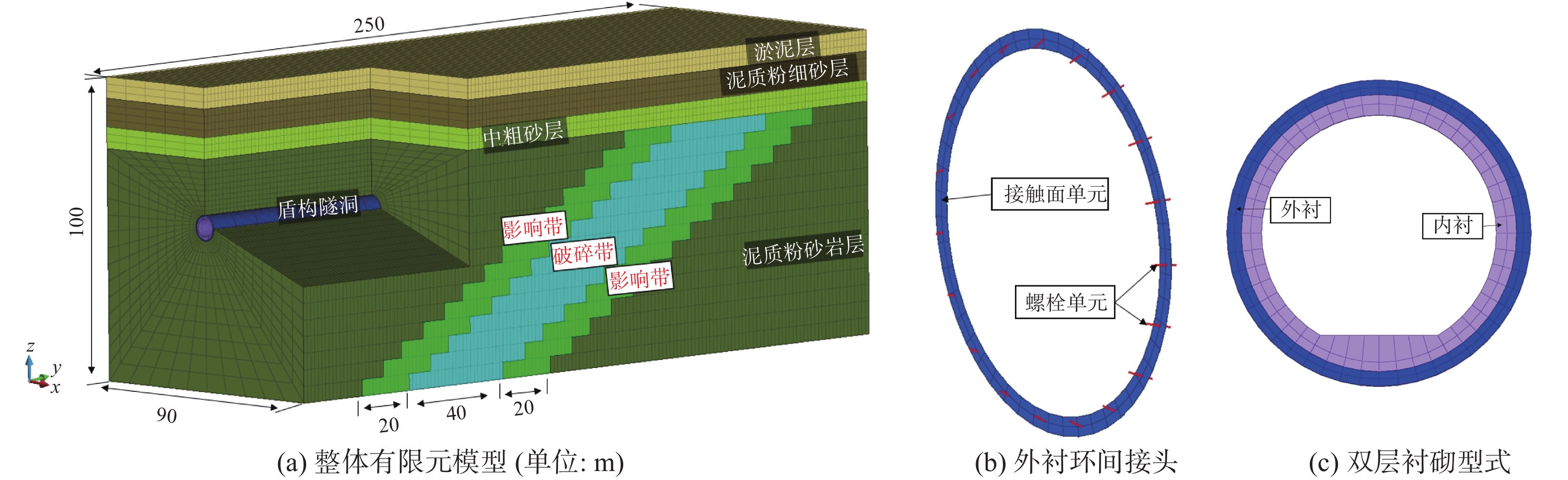
选取某工程盾构隧洞穿越断层破碎带处为典型地质段(长度250 m),用以研究不良地质情况对输水隧洞纵向变形的影响。本段线路内盾构隧洞采用双层衬砌结构,外衬采用C55预制钢筋混凝土,外径8.3 m,内径7.5 m,环宽1.6 m,环间通过斜螺栓连接。螺栓采用M30不锈钢螺栓,产品等级为A4-70级,预紧力为128 kN。内衬采用C50预应力混凝土,厚度0.55 m。在隧洞上部外衬内侧设有300°范围的隔离层。根据沿线地质勘测,选取的典型地质段从上到下分为4个地层:淤泥层、泥质粉细砂层、中粗砂层和泥质粉砂岩层(弱风化)。区域内隧洞穿越一破碎带,倾角约50°,宽度约40 m,为黄褐色断层泥等充填,风化剧烈。在断层破碎带左右均存在断层影响带,宽度约20 m。地层及隧洞材料参数见表2。
表 2 材料参数Table 2. Material parameters名称 重度/(kN·m−3) 弹性模量/MPa 泊松比 外衬 24.3 3.55×104 0.20 内衬 24.2 3.45×104 0.20 淤泥层 16.7 2.85 0.35 泥质粉细砂层 20.9 5.91 0.30 中粗砂层 21.3 6.21 0.25 泥质粉砂岩层 25.9 6.81×103 0.24 断层破碎带 21.2 150.00 0.35 断层影响带 21.3 2.50×103 0.30 考虑到本文研究重点为隧洞纵向变形,故仅考虑环间接头的接触模拟,将管片沿环向简化为均质圆环,根据修正惯用法理论,通过对圆环的刚度进行折减来考虑管片接头的影响,刚度有效率取0.8,计算中按折减混凝土管片弹性模量考虑[12]。假定外衬和基岩之间按完好粘结,同时混凝土外衬和内衬按底部60°范围粘结模型考虑[18]。混凝土外衬、内衬及地层均采用等参单元进行离散,采用线弹性本构模型模拟。外衬环间接缝处设置非线性接触面单元,按传压不传拉模拟,初始法向和切向刚度参考文献分别取为3.585×1010 N/m3和2.03×109 N/m3,接缝面的摩擦系数取0.5[19-20]。外衬环间沿环向均匀分布的19根螺栓采用埋置梁单元模拟。有限元计算模型如图8所示,节点总数339 354个,单元总数274 216个。
3.1 计算工况及荷载
本文分析通水运行工况下盾构隧洞穿越断层破碎带不良地质条件下纵向变形响应。采用金尼克弹性侧压理论模拟土体自重应力,侧压系数依据地勘报告取0.35。外水压力按50 m水头计算,内水设计压力1.35 MPa,且考虑隧洞内水重及衬砌自重。内衬预应力施加采用等效荷载法,施加的螺栓预紧力为轴力。计算模型上表面为自由面,对模型四周及底部边界均约束法向位移。
3.2 计算结果及分析
计算工况下隧洞在破碎带区域附近外衬纵向变形分布见图9。从图9可以看出,在均质基岩处隧洞几乎没有纵向变形,在影响带内变形微小,且都集中在靠近破碎带一侧,变形主要发生在破碎带内及破碎带和影响带的交界面处。由局部放大图可以看出变形主要为环间缝的张开和错台变形。
3.2.1 环间接缝张开及错台
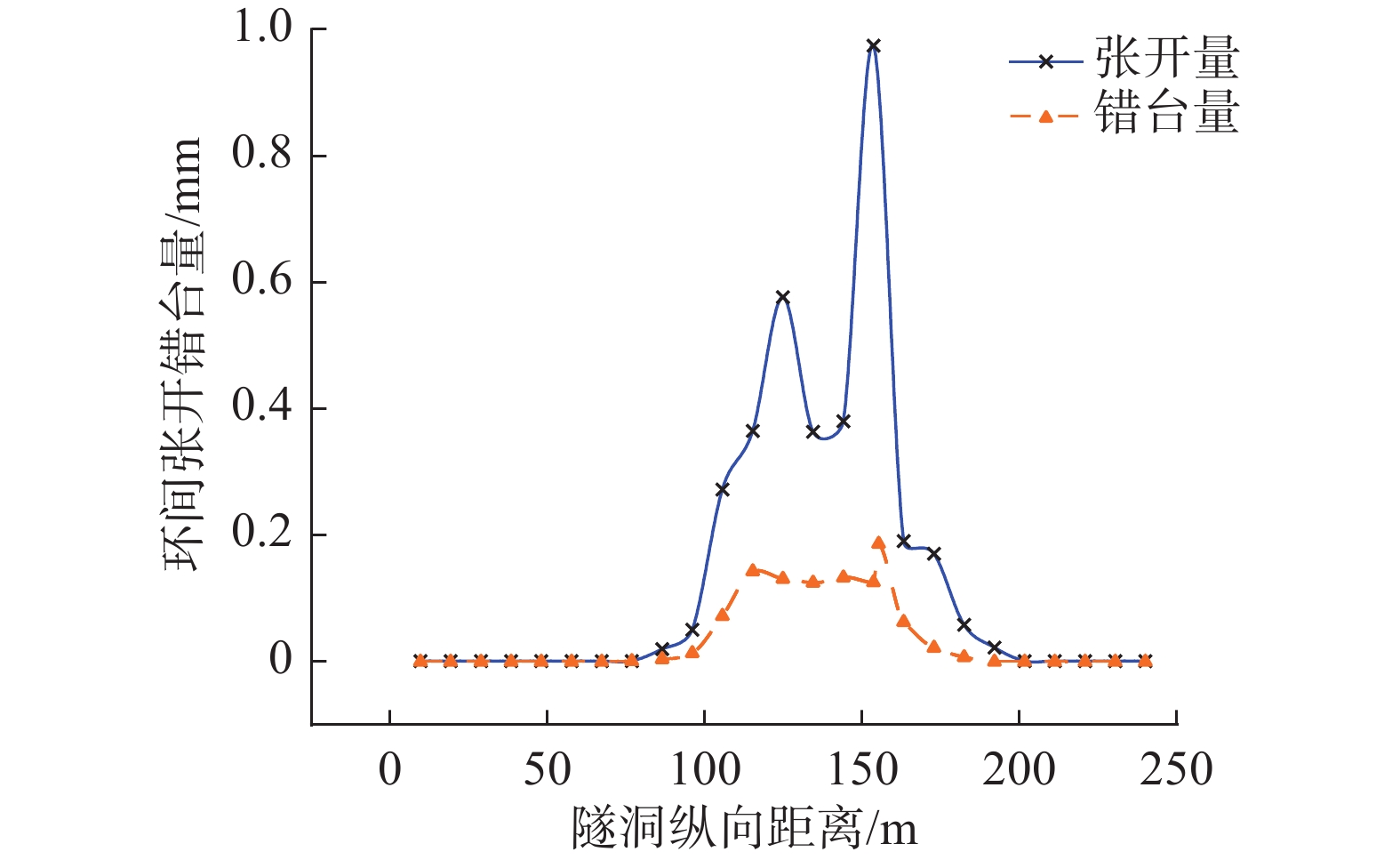
沿隧洞轴向分别提取外衬每个环间接缝的最大张开和错台量值,得到外衬张开错台变形沿程分布规律如图10所示。从图10可知,在均质基岩段,外衬结构几乎没有张开错台变形,变形主要集中在破碎带区域附近。 外衬环间张开和错台量沿程存在两个峰值,均出现在破碎带和两侧影响带的交界面附近,这表明在围岩弹模骤减的交界面区域,环间会产生较大的张开错台变形。环间张开沿程最大值为0.97 mm,错台沿程最大值为0.19 mm,其所在位置的环间缝的张开错台变形分布如图11所示,张开和错台变形主要发生位置相近,均在拱底外侧偏右位置。
本工程盾构隧洞接缝防水性能试验研究结果表明:衬砌在接缝张开量6 mm、错台量15 mm条件下,其防水能力仍达到了1.6 MPa。由以上隧洞纵向变形计算结果可得,衬砌环间最大张开量为0.97 mm,最大错台量为0.19 mm。本文选取段内水压1.35 MPa,这表明该工况下隧洞衬砌接缝防水性能满足工程设计防水要求。
3.2.2 螺栓应力
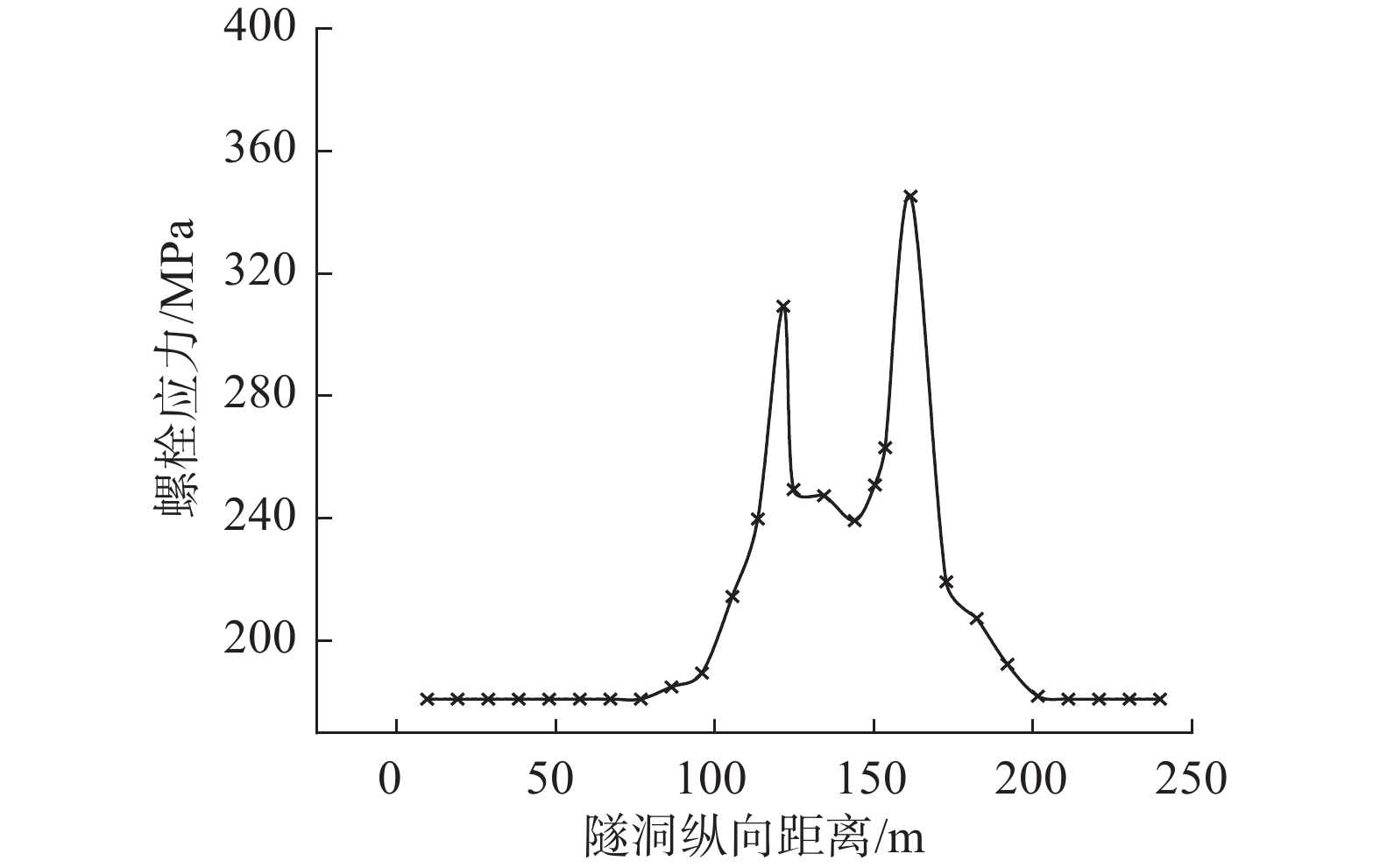
沿隧洞轴向分别提取外衬每个环间接缝19个连接螺栓中的最大拉应力值,得到螺栓应力沿程分布规律如图12所示。应力值沿程出现两个峰值,均在破碎带和影响带交界面附近,与外衬环间缝张开错台变形规律相符。预紧力导致的螺栓初始拉应力为181 MPa,在均质基岩区域螺栓最大应力均在181 MPa左右,这表明在均质基岩内螺栓状态未受侵扰,应力稳定,与外衬在均质基岩内未发生张开错台变形结果相符。
隧洞在破碎带和影响带区域螺栓应力明显大于均质基岩区域,螺栓沿程最大拉应力值为345.2 MPa,低于螺栓的屈服强度450 MPa,满足设计要求。此处环间接头螺栓应力分布如图13所示,螺栓应力在拱底右侧较大,与外衬在相近位置张开错台变形较大结果相符。
4. 结 语
基于埋置梁广义位移法和考虑传压不传拉的接触面单元,建立了能同时考虑接缝面的接触非线性、不同螺栓型式及其受力特性的环间接头有限元模拟方法。以此为基础建立盾构隧洞纵向三维分析模型,能合理准确地反映出盾构隧洞在复杂地质条件下的力学响应。对某穿越断层破碎带处盾构隧洞工程采用上述模型进行了计算分析,结果表明在均质基岩中隧洞结构稳定,几乎无变形;当隧洞进入断层破碎带区域,衬砌局部出现张开、错台变形,螺栓应力增大,但均在设计控制范围之内。研究可为工程安全建设及运行提供科学依据。
-
表 1 有限元法和解析法计算结果
Table 1 Calculation results of finite element method and analytical method
分类 中性轴
位置/°环间最大
张开量/mm螺栓最大
拉应力/MPa有限元数值解 约22 0.52 475.20 理论解析解 23.93 0.51 470.14 表 2 材料参数
Table 2 Material parameters
名称 重度/(kN·m−3) 弹性模量/MPa 泊松比 外衬 24.3 3.55×104 0.20 内衬 24.2 3.45×104 0.20 淤泥层 16.7 2.85 0.35 泥质粉细砂层 20.9 5.91 0.30 中粗砂层 21.3 6.21 0.25 泥质粉砂岩层 25.9 6.81×103 0.24 断层破碎带 21.2 150.00 0.35 断层影响带 21.3 2.50×103 0.30 -
[1] 龚林金, 任锐, 王亚琼, 等. 隧道斜穿不同倾角断层破碎带围岩变形特征分析[J]. 公路,2021,66(7):313-319 GONG Linjin, REN Rui, WANG Yaqiong, et al. Analysis on deformation characteristics of surrounding rock of tunnel crossing fault fracture zone with different dip angles[J]. Highway, 2021, 66(7): 313-319. (in Chinese)
[2] 张贵金, 杨松林. 深埋大直径无压引水隧洞基于流变的风险分析[J]. 水利水运工程学报,2005(1):15-22 doi: 10.3969/j.issn.1009-640X.2005.01.003 ZHANG Guijin, YANG Songlin. Risk analysis of deep-buried free-flow large-diameter tunnel based on surrounding rock rheology[J]. Hydro-Science and Engineering, 2005(1): 15-22. (in Chinese) doi: 10.3969/j.issn.1009-640X.2005.01.003
[3] 鄢建华, 洪晓林, 汤雷. 挤压性围岩软化模型及在大变形分析中的应用[J]. 水利水运工程学报,2005(2):28-31 doi: 10.3969/j.issn.1009-640X.2005.02.005 YAN Jianhua, HONG Xiaolin, TANG Lei. Softening model for squeezed surrounding rock and its application in large deformation analyses[J]. Hydro-Science and Engineering, 2005(2): 28-31. (in Chinese) doi: 10.3969/j.issn.1009-640X.2005.02.005
[4] 张景. 盾构隧道环间接头抗弯刚度计算及其影响因素研究[J]. 现代隧道技术,2020,57(4):104-112 ZHANG Jing. Study on calculations and influence factors of bending stiffness of segment ring joints of shield tunnels[J]. Modern Tunnelling Technology, 2020, 57(4): 104-112. (in Chinese)
[5] 张景, 何川, 耿萍, 等. 盾构隧道环间接头弯曲状态非线性研究[J]. 工程力学,2018,35(11):35-44 doi: 10.6052/j.issn.1000-4750.2017.08.0624 ZHANG Jing, HE Chuan, GENG Ping, et al. Study on bending state nonlinearity of shield-tunnel ring joints[J]. Engineering Mechanics, 2018, 35(11): 35-44. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.08.0624
[6] 闫治国, 丁文其, 沈碧伟, 等. 输水盾构隧道管片接头力学与变形模型研究[J]. 岩土工程学报,2011,33(8):1185-1191 YAN Zhiguo, DING Wenqi, SHEN Biwei, et al. Structural model for radial joints of water-conveyance shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(8): 1185-1191. (in Chinese)
[7] 志波由紀夫, 川島一彦, 大日方尚巳, 等. シールドトンネルの耐震解析に用いる長手方向覆工剛性の評価法[J]. 土木学会論文集, 1988(398): 319-327. SHIBA Yukio, KAWASHIMA Kazuhiko, OBINATA Naomi, et al. An evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analyses[J]. Journal of Japan Society of Civil Engineers, 1988(398): 319-327. (in Japanese)
[8] 小泉淳, 村上博智, 石田智朗, 等. 急曲线施工用セタヌトの设计法につぃて[J]. 土木学会論文集, 1992, 6: 111-120. KOIZUMI Jun, MURAKAMI Hirotomo, ISHIDA Tomorowo, et al. Study on segment design in sharp curved line construction[J]. Journal of Japan Society of Civil Engineers, 1992, 6: 111-120. (in Japanese)
[9] 张文杰, 徐旭, 李向红, 等. 广义的盾构隧道纵向等效连续化模型研究[J]. 岩石力学与工程学报, 2009, 28(增刊2): 3938-3944. ZHANG Wenjie, XU Xu, LI Xianghong, et al. Research on generalized longitudinal equivalent continuous model of shield tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Suppl 2): 3938-3944. (in Chinese)
[10] 李翔宇, 刘国彬, 杨潇, 等. 基于修正纵向等效连续化模型的隧道变形受力研究[J]. 岩土工程学报,2014,36(4):662-670 doi: 10.11779/CJGE201404010 LI Xiangyu, LIU Guobin, YANG Xiao, et al. Deformation and stress of tunnel structures based on modified longitudinal equivalent continuous model[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 662-670. (in Chinese) doi: 10.11779/CJGE201404010
[11] YU H T, CAI C, BOBET A, et al. Analytical solution for longitudinal bending stiffness of shield tunnels[J]. Tunnelling and Underground Space Technology, 2019, 83: 27-34. doi: 10.1016/j.tust.2018.09.011
[12] 桑运龙, 刘学增, 张强. 基于螺栓-凹凸榫连接的地铁盾构隧道管片环缝接头刚度分析及应用[J]. 隧道建设(中英文),2020,40(1):19-27 SANG Yunlong, LIU Xuezeng, ZHANG Qiang. Stiffness analysis and application of segment annular joint based on bolt-concave and convex tenon connection in metro shield tunnel[J]. Tunnel Construction, 2020, 40(1): 19-27. (in Chinese)
[13] 耿萍, 陈枰良, 陈昌健, 等. 考虑接触非线性的盾构隧道纵向分析模型及其应用[J]. 同济大学学报(自然科学版),2021,49(6):759-769 doi: 10.11908/j.issn.0253-374x.21139 GENG Ping, CHEN Pingliang, CHEN Changjian, et al. Longitudinal analysis model of shield tunnel considering contact nonlinearity and its application[J]. Journal of Tongji University (Natural Science), 2021, 49(6): 759-769. (in Chinese) doi: 10.11908/j.issn.0253-374x.21139
[14] 苏宗贤, 何川. 盾构隧道纵向变形附加内力的壳-弹簧-接触模型数值分析[J]. 现代隧道技术,2015,52(6):70-76 SU Zongxian, HE Chuan. Shell-spring-contact model based numerical analysis of additional internal forces induced by the longitudinal deformation of a shield tunnel[J]. Modern Tunnelling Technology, 2015, 52(6): 70-76. (in Chinese)
[15] 刘学增, 蔡光远, 杨帆, 等. 破碎围岩错缝拼装盾构隧道结构承载性能与变形控制指标[J]. 中国公路学报,2017,30(8):57-65 doi: 10.3969/j.issn.1001-7372.2017.08.006 LIU Xuezeng, CAI Guangyuan, YANG Fan, et al. Structural bearing behavior and deformation controlling indicators for staggered jointed shield tunnel lining in fractured surrounding rock[J]. China Journal of Highway and Transport, 2017, 30(8): 57-65. (in Chinese) doi: 10.3969/j.issn.1001-7372.2017.08.006
[16] 谢小玲, 苏海东, 林绍忠. 穿黄隧洞纵向变形三维有限元分析[J]. 长江科学院院报,2010,27(7):60-64 doi: 10.3969/j.issn.1001-5485.2010.07.013 XIE Xiaoling, SU Haidong, LIN Shaozhong. Analysis on longitudinal deformation of tunnel crossed Yellow River by 3-D finite element[J]. Journal of Yangtze River Scientific Research Institute, 2010, 27(7): 60-64. (in Chinese) doi: 10.3969/j.issn.1001-5485.2010.07.013
[17] 邵炜, 金峰, 王光纶. 用于接触面模拟的非线性薄层单元[J]. 清华大学学报(自然科学版),1999,39(2):34-38 doi: 10.3321/j.issn:1000-0054.1999.02.009 SHAO Wei, JIN Feng, WANG Guanglun. Nonlinear thin layer element for modeling interface[J]. Journal of Tsinghua University (Science and Technology), 1999, 39(2): 34-38. (in Chinese) doi: 10.3321/j.issn:1000-0054.1999.02.009
[18] 姚广亮, 陈震, 严振瑞, 等. 高内水压盾构隧洞预应力混凝土内衬结构受力分析[J]. 人民长江,2020,51(6):148-153 YAO Guangliang, CHEN Zhen, YAN Zhenrui, et al. Analysis on stress of pre-stressed lining of shield tunnel under high internal pressure[J]. Yangtze River, 2020, 51(6): 148-153. (in Chinese)
[19] 张振宇, 李豪杰, 李朝君, 等. 盾构管片接缝传力垫层的接触特性试验研究[J]. 隧道建设(中英文),2017,37(11):1404-1408 ZHANG Zhenyu, LI Haojie, LI Chaojun, et al. Experimental study of contact characteristics of rubber cushion used in shield segment joints[J]. Tunnel Construction, 2017, 37(11): 1404-1408. (in Chinese)
[20] 郭瑞, 何川, 苏宗贤, 等. 盾构隧道管片接头抗剪力学性能研究[J]. 现代隧道技术,2011,48(4):72-77 doi: 10.3969/j.issn.1009-6582.2011.04.013 GUO Rui, HE Chuan, SU Zongxian, et al. Study of shearing mechanical properties of segment joints of shield tunnels[J]. Modern Tunnelling Technology, 2011, 48(4): 72-77. (in Chinese) doi: 10.3969/j.issn.1009-6582.2011.04.013
-
期刊类型引用(1)
1. 朱悦悦,刘成. 输水隧洞灌浆式预应力衬砌结构承载机理研究. 水利水运工程学报. 2022(06): 146-155 .  本站查看
本站查看
其他类型引用(1)



 Email Alerts
Email Alerts RSS
RSS
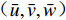
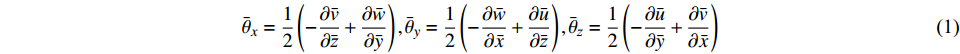
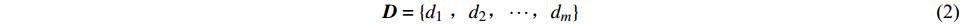
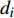
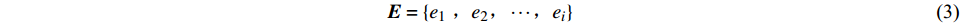


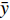

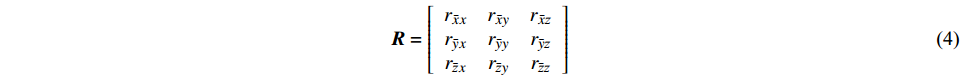

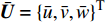

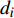

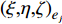

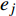

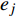
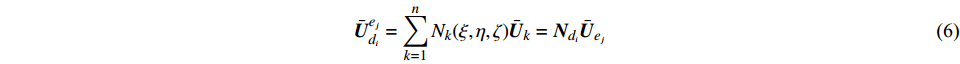
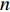
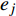
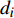
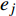
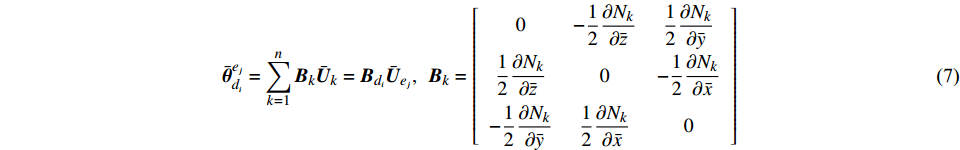
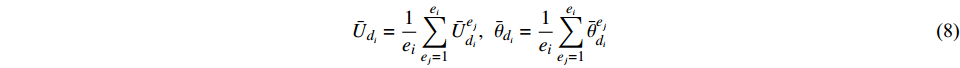
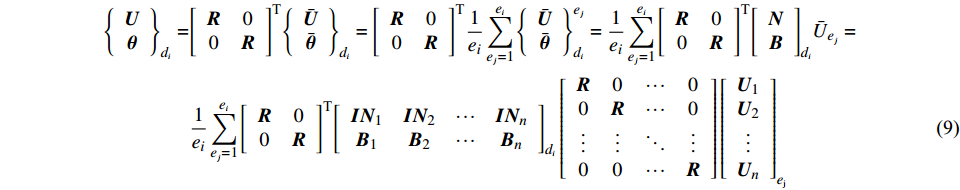
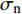
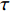

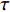
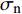

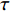

 下载:
下载: