Temperature gradient analysis of rectangular aqueduct transverse section under the effect of large temperature difference
-
摘要: 渡槽在服役期间经历长期变温差循环作用,势必引起渡槽混凝土产生微裂纹等劣化,降低渡槽安全性。渡槽设计无专门规范,相关规范对渡槽是否考虑温度荷载也无明确指导意见。以新疆某矩形渡槽为例,通过有限元软件计算渡槽横截面温度场,分析其分布规律,探讨渡槽温度梯度及不同桥梁设计规范在渡槽设计中的适用性。研究表明:该渡槽通水时夏季横截面最大竖向正温差为35.8 ℃,不通水时为24.5 ℃;冬季通水时最大竖向负温差为−11.5 ℃,不通水时为−7.8 ℃。渡槽横向最大正温差为18.5 ℃,最大负温差为−8.4 ℃;较大的竖向与横向温度梯度会产生较大的温度应力,在设计中应给予考虑。实例竖向温度梯度与各种桥梁规范推荐的竖向温度梯度模式形式相似,但特征值存在较大差异,桥梁规范中的温度梯度模式不宜直接应用于渡槽温度应力分析,渡槽温度场宜根据槽身结构形式和运行工况计算确定。Abstract: During the operation period, the aqueduct experiences the cyclic fatigue effect of temperature variation for long term, which may cause the deterioration of the concrete of the aqueduct, such as micro-crack, and gradually reduce the safety degree of the aqueduct. There is no specific design code for aqueduct design, and other relevant design codes don’t provide clear guidance on whether to consider thermal effects for aqueduct. Taking a rectangle aqueduct in Xinjiang as an example and through the finite element software, the aqueduct temperature field is obtained and its distribution law is analyzed. Furthermore, the applicability of vertical temperature gradient pattern recommended by bridge codes in aqueduct design is discussed. The results show that the maximum vertical positive temperature difference in summer is 35.8 ℃ when the aqueduct is running, and 24.5 ℃ when the aqueduct is not running. In winter, the maximum vertical negative temperature difference is −15.1 ℃ with running water, and −7.8 ℃ without running water. The maximum transverse positive temperature difference of the aqueduct is 18.5 ℃ and the maximum transverse negative temperature difference is 11.2 ℃. Large vertical and transverse temperature gradient will produce large temperature stress, which should be taken into account in design. The vertical temperature gradient of the example is similar to the vertical temperature gradient modes recommended by various bridge codes, but there are large differences in the characteristic values, indicating that the temperature gradient modes of bridge codes may not be directly applied to the temperature stress analysis of the aqueduct. The temperature field of aqueduct should be calculated and determined according to the structural form and operation conditions of the aqueduct.
-
Keywords:
- aqueduct /
- large temperature difference /
- temperature field /
- temperature gradient /
- design codes
-
渡槽是输送渠道水流跨越河渠、溪谷、洼地及道路的重要交叉建筑物。渡槽槽身属于薄壁结构,极易因温度应力导致开裂破坏[1]。槽身外边界温度随环境气温变化,而槽内水体大部分来自水库,水温相对稳定,这使得渡槽在夏季运行时槽内水温常低于环境气温,而在冬季运行时槽内水温则又常高于气温,加之外界气温变化影响,槽身内自然形成年周期性温差循环。槽身为空间结构,在太阳日照辐射和地面反射等作用下,沿高度、宽度和壁厚方向自然形成温差,产生自约束温度应力。同时,由于混凝土属于多相复合材料,骨料和砂浆的热膨胀系数不同[2],导致热变形不协调,极易在骨料和砂浆的界面产生微裂纹。由此,在昼夜和年循环交变大温差作用下,渡槽混凝土极易形成微裂纹,长期作用将导致宏观裂缝,引起混凝土性能劣化,降低渡槽的安全性。
随着我国南水北调工程的开展,渡槽的温度效应问题备受关注。王长德等[3]将槽身在运行期的温度效应分为年内变化的长期温度应力、日正常温度变化和日温度骤降引起的短期温度应力,在日正常温度变化中又分为夏季和冬季两种工况进行温度应力分析,分析后指出冬季环境温降对槽身底板危害较大;王潘绣等[4]重点研究夏季运行期因突降暴雨导致环境温度降低引起的槽身开裂风险问题;赵山等[5]开展了寒潮作用下U形槽身温降效应研究。另外,已有大量文献分析了槽身在日照条件下的温度场和温度应力,探求温度分布模式等[6-7]。上述研究多针对具体工程根据温差产生的局部最大拉应力来分析温度效应,仅是渡槽运行期某种特殊工况或最不利工况,文献[6-7]虽然应用了桥梁规范推荐的温度梯度模式,但是否适用及温差代表值的选取并没有深入讨论,也未系统研究渡槽槽身结构形式对其温度场的影响。
另外,渡槽槽身截面形式类似道路桥梁的箱形截面,关于混凝土箱梁桥的温度作用及效应研究已有较多研究成果[8-11],部分成果及建议已纳入公路桥涵设计规范[12]。然而渡槽槽身截面形式及槽内环境与道路桥梁的箱形截面有一定差异,影响其温度分布。首先,渡槽槽身顶板外伸翼缘长度远小于桥梁的箱梁或没有顶板,其遮阴效果几乎为零,而桥梁的箱梁一般有较长的悬臂,对腹板的遮阴效果明显;第二,槽身内经常有流动的水体,会带走槽壁的热量,而桥梁箱梁内部充满静止的空气,二者内部热边界条件不同;第三,槽身若不设顶板,部分槽内壁受阳光直射,其温度边界条件与外壁相同,加之槽内水流边界的复杂性,导致槽身温度场更加复杂。渡槽设计尚无专门的设计规范,大型渡槽工程设计多参考桥梁设计规范,其合理性需要论证。因此,本文从水工渡槽结构和运行特点出发,开展大温差作用下渡槽槽身纵向、横向温差和纵向温度梯度分析,探讨桥梁设计规范在渡槽设计中的适用性,为渡槽工程设计、运行期安全评估提供理论支撑。
1. 渡槽热传导理论模型
处于运行期的渡槽,经过天然散热,水化热温升完全消失,槽身温度取决于环境气温、日照和槽内水体等。由于渡槽截面沿纵向(跨度方向)一般不变,故在分析渡槽温度场时假定截面温度分布沿渡槽纵向不变,即可取任一横截面为研究对象,简化为平面热传导问题进行分析,热传导方程[13]为:
$$ {{\partial T}}/{{\partial t}} = \beta \left( {{{{\partial ^2}T}}/{{\partial {x^2}}} + {{{\partial ^2}T}}/{{\partial {y^2}}}} \right) $$ (1) 式中:T为温度;t为时间;β
为混凝土导温系数,β=λ/(ρc),λ为导热系数,ρ为渡槽混凝土的密度,c为比热容; x、y为坐标值。 确定初始条件时可取渡槽所在地当日平均温度,待温度稳定后形成的温度场即为正式计算初始条件,本文计算中,根据计算目标日,提前3 d计算。
渡槽槽身表面受到太阳日照辐射、环境气温、水体温度、长波辐射的影响,槽壁与其接触的空气和水体之间存在热量交换。渡槽的热边界包括槽身外壁与大气的对流换热、太阳辐射换热及结构本身与外界的长波辐射换热、槽内壁与槽内水体的对流换热,外壁热边界条件[14]可表示为:
$$ \lambda {{\partial T}}/{{\partial n}}\left| {_\Gamma } \right.{\text{ = }}\alpha {I_\phi } + {h_{\text{r}}}\left( {{T_{\text{a}}} - {T_{\text{s}}}} \right) + {h_{\text{c}}}\left( {{T_{\text{a}}} - {T_{\text{s}}}} \right) $$ (2) 式中:等号右侧第1、2、3项分别代表太阳辐射、辐射换热和对流换热的热流密度;α为太阳辐射吸收系数,取值范围为0.5~0.7 [15],本文取0.65;Iϕ为垂直于被照射表面的日照辐射强度;辐射换热热流密度占比较小,且变化幅度小,故采用简化方法进行计算[16];hr和hc分别为辐射换热系数和对流换热系数;Ta为大气温度;Ts为渡槽表面温度。
引入工程中便于测试的综合换热系数,式(2)可转化为:
$$ \lambda {{\partial T}}/{{\partial n}}\left| {_\Gamma } \right.{\text{ = }}\left( {{h_{\text{r}}} + {h_{\text{c}}}} \right)\left( {{{\alpha {I_\phi }}}/({{{h_{\text{r}}} + {h_{\text{c}}}}}) + {T_{\text{a}}} - {T_{\text{s}}}} \right){\text{ = }}h\left( {T_{\text{a}}^* - {T_{\text{s}}}} \right) $$ (3) $$ T_{\text{a}}^*{\text{ = }}{{\alpha {I_\phi }}}/{h} + {T_{\text{a}}} $$ (4) $$ h{\text{ = }}{{{h_{\text{r}}} + {h_{\text{c}}}}}{\text{ = }}12.47 + 3.33{v_0} $$ (5) 式中:h为综合换热系数,可根据风速近似计算[17];v0为风速;
$ {T_{\text{a}}}^* $ 为综合大气环境温度。当槽内通水时,由于水与渡槽混凝土间的换热系数较大,可按第一类边界条件处理,直接取渡槽内壁的温度等于水体温度,也可按第三类边界条件,取较大的换热系数,以对流换热的形式进行计算,本文按第三类边界条件进行处理,换热系数取为120 W/(m2·℃)。
计算工况分为槽内通水和不通水两种。当槽内不通水时,无顶板的渡槽内壁边界条件等同外壁,以环境气温为箱体内部温度,同时考虑渡槽腹板的遮阴效应,槽内表面与周围环境的综合换热系数近似取外表面与周围环境的综合换热系数;有顶板渡槽的箱体内部温度可取当日的平均气温。通过有限元法计算比较,即使将渡槽内表面与箱内环境的综合换热系数增加或减少50%,对温度计算结果的影响最大也不会超过1 ℃,因此这种简化处理方法是可行的[11]。
2. 工程实例
2.1 实例概况与参数选取
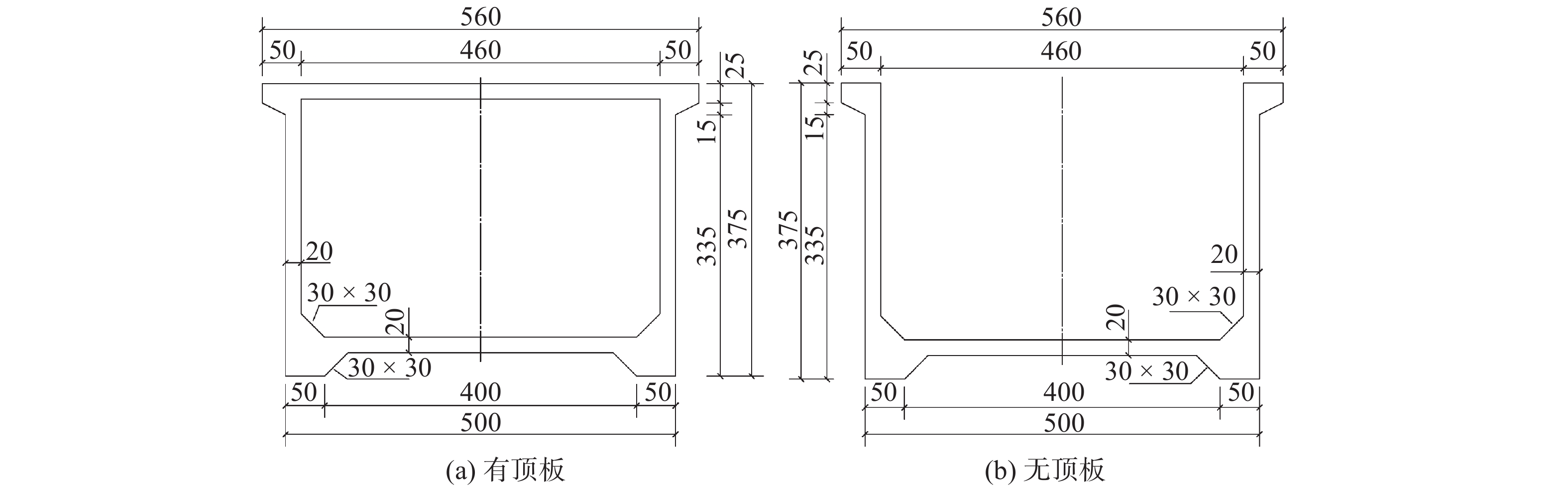
选取新疆地区某渡槽[18]进行计算。矩形渡槽高3.75 m、宽5.00 m,腹板与顶板壁厚均为0.20 m,其他槽身断面尺寸见图1。槽内满槽水深为2.80 m,槽内水来自近处的水库,以某水库水温为依据,在冬季取为4 ℃,夏季取为10 ℃[19]。根据该渡槽所在地2011年6月至2012年9月气象实测数据获得每日每小时的环境温度、风速、太阳辐射、风速等基础数据,分别在渡槽不同表面与空气接触边界处按式(3)~(5)计算。
因渡槽东西走向时,北侧(阴面)腹板所受到的太阳辐射强度较小,此时渡槽易产生较大竖向温度梯度,故取东西走向渡槽进行分析。为研究顶板的影响,按设顶板封闭式和不设顶板开敞式两种结构形式进行计算,每种形式渡槽又分为槽内通水和不通水两种工况。混凝土相关热力学参数取值[20]为:密度2 456 kg/m3,比热容958 J/ (kg·℃),导热系数2.96 J/ (m·s·℃)。渡槽全部采用平面四边形四结点单元,有顶板渡槽共剖分1 966个节点,1 630个单元;无顶板渡槽共剖分1 511个节点,1 262个单元。
计算步骤:(1)根据渡槽年平均温度变化规律分别确定正、负温差最大时段;(2)在最大时段内,根据日最高温度、日最低温度、每小时风速等,通过计算得到每日气象平均温度、平均风速,综合换热系数等数据,再以日最高温度、气象平均温度、日最低温度为渡槽的外边界条件,计算渡槽横截面温度分布,由此得到相对日温差最大的时段,即有顶板的渡槽夏季为2011年7月10—12日、冬季为2012年2月2—4日,无顶板渡槽夏季为2011年7月12—14日、冬季为2012年2月18—20日;(3)以上述4个时段为基础,再详细分析渡槽日温度场变化规律。
2.2 竖向温度分布
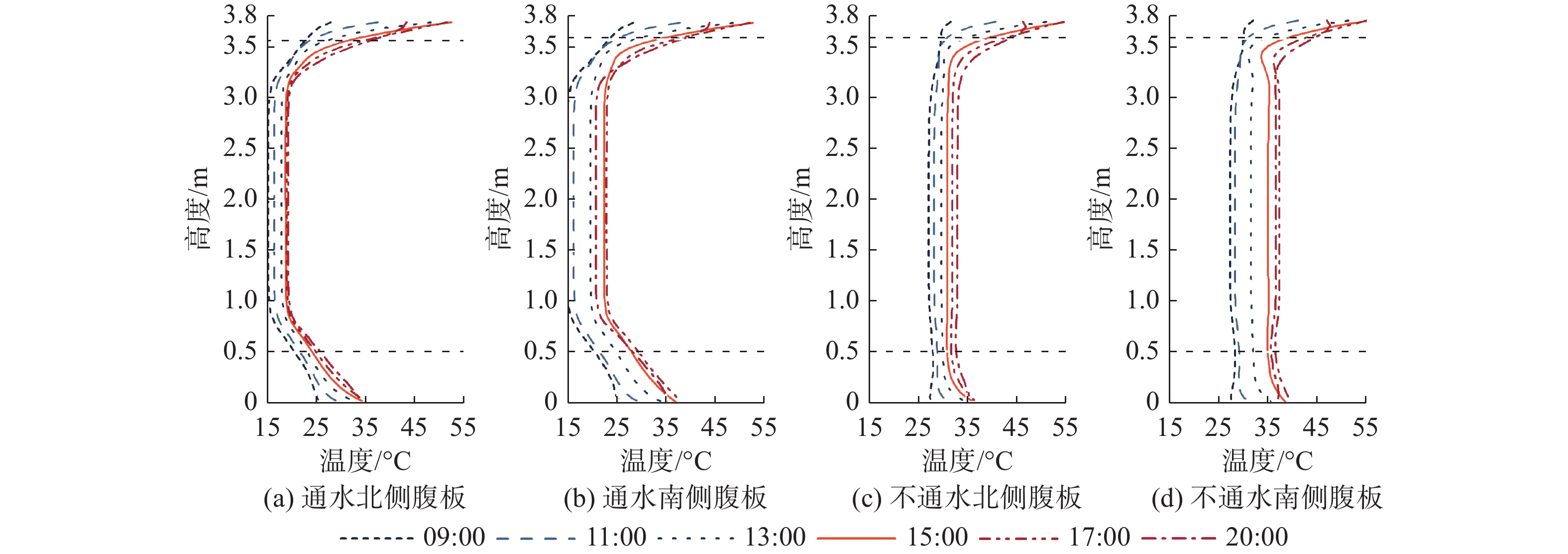
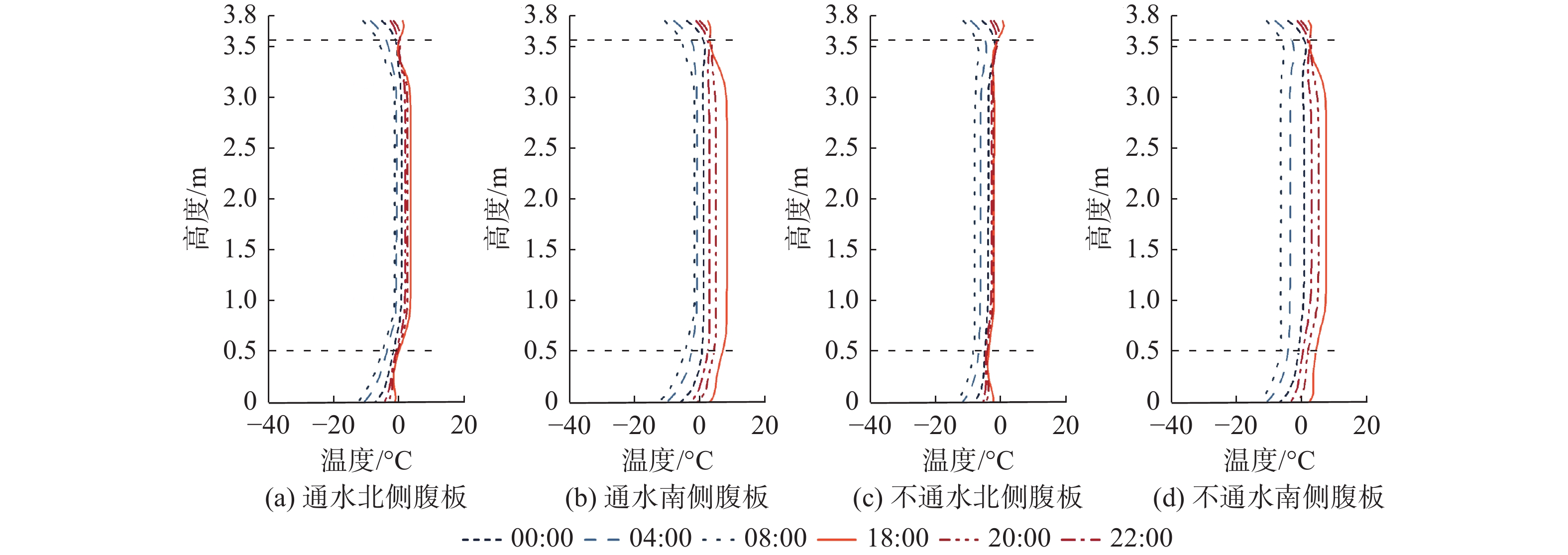
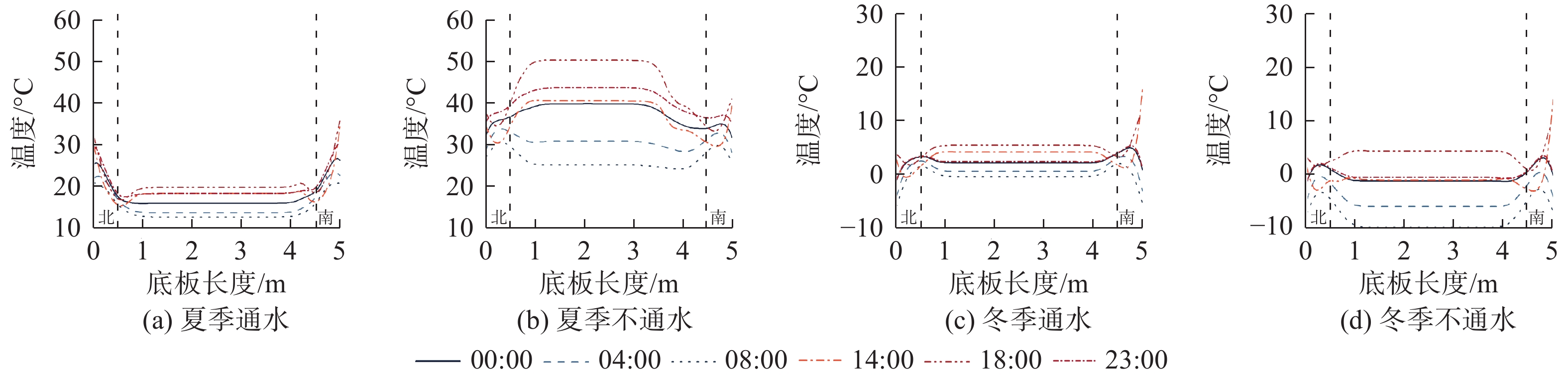
有顶板渡槽夏季升温和冬季降温竖向温度分布见图2和3。无顶板时规律相似,在此仅列出其温差变化规律(表1)。图中两条水平虚线外分别为渡槽的顶板与底板。为陈述方便,将无顶板渡槽的腹板顶部相同厚度混凝土(0.2 m)视为无顶板渡槽的顶板。由图2和3可见,各工况下日内腹板温度变化均小于顶板和底板端部的变化幅度。通水时,夏季无论渡槽有无顶板,顶板与底板端部的温度均高于腹板;冬季有顶板渡槽顶板与底板端部的温度均低于腹板,无顶板渡槽底板端部温度均低于腹板,而顶板端部温度在12:00—20:00高于腹板。不通水时,渡槽在夏季20:00至次日08:00底板处温度会低于腹板,在冬季12:00—20:00顶板端部温度会高于腹板。定义渡槽顶板、底板的温度与腹板中心点温度之差为顶板、底板(与腹板)的竖向温差。不同工况下渡槽顶板、底板的夏季最大竖向正温差、冬季最大竖向负温差见表1。
表 1 渡槽最大竖向正(负)温差Table 1. Maximum vertical positive (negative) temperature difference of aqueduct单位:℃ 运行工况 渡槽形式 腹板位置 顶板 底板 夏季通水 有顶板渡槽 南侧腹板 30.5 15.2 北侧腹板 33.8 16.5 无顶板渡槽 南侧腹板 31.0 18.8 北侧腹板 35.8 18.7 夏季不通水 有顶板渡槽 南侧腹板 20.7 4.6 北侧腹板 24.5 5.5 无顶板渡槽 南侧腹板 16.1 4.9 北侧腹板 20.7 4.6 冬季通水 有顶板渡槽 南侧腹板 −9.0 −10.9 北侧腹板 −9.6 −11.5 无顶板渡槽 南侧腹板 −8.5 −7.7 北侧腹板 −8.6 −8.3 冬季不通水 有顶板渡槽 南侧腹板 −3.4 −5.7 北侧腹板 −4.9 −7.8 无顶板渡槽 南侧腹板 −3.8 −5.0 北侧腹板 −2.2 −7.6 从表1可见:渡槽在通水时的最大竖向正(负)温差远超不通水时,有顶板渡槽顶板、底板的竖向最大温差绝对值与无顶板渡槽差异较小;不通水时夏季渡槽顶板最大温差远超冬季顶板最大温差的绝对值;渡槽在通水时夏季最大正温差为35.8 ℃,冬季最大负温差为−11.5 ℃;不通水时渡槽最大正温差为24.5 ℃,最大负温差为−7.8 ℃。所以,设计时应考虑渡槽竖向温度分布所带来的不利影响。
2.3 横向温度分布
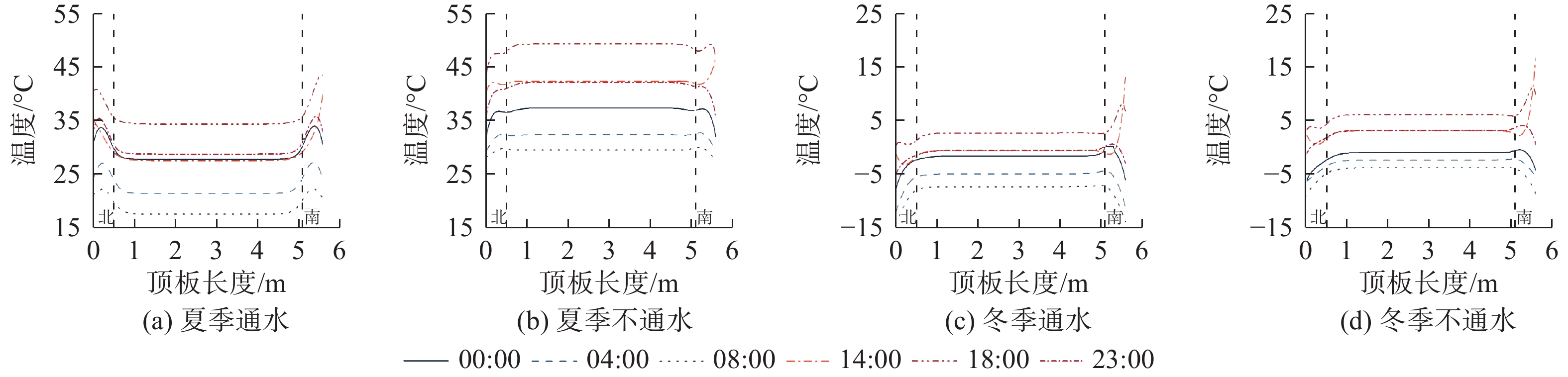
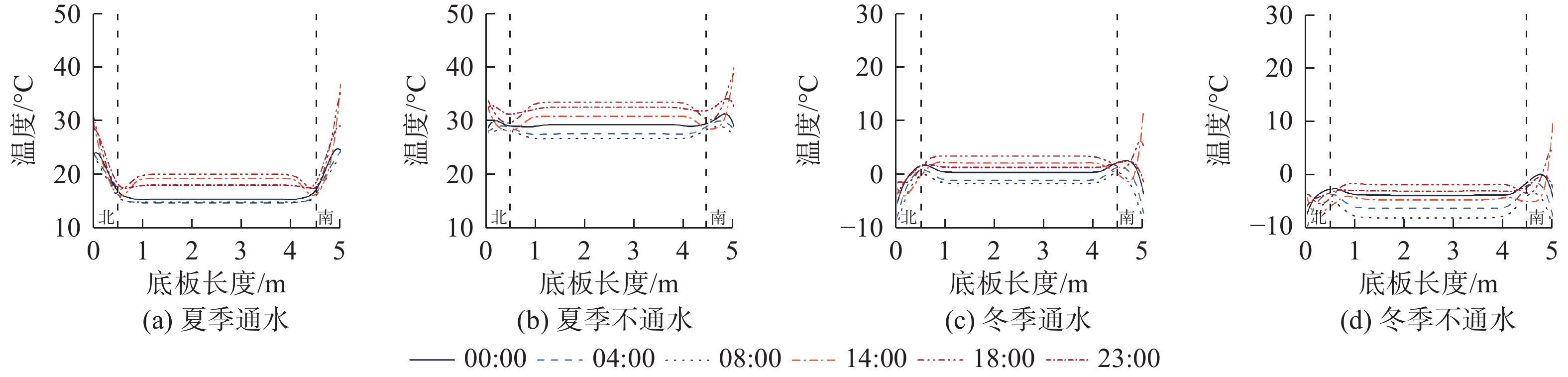
因渡槽两侧腹板受到的太阳辐射强度不同,使得渡槽同时存在较大的横向温度梯度。不同形式和工况下的温度分布见图4~6。图4~6中两条竖直虚线之间为位于两侧腹板间的顶板或底板,从图4~6可以看出,顶板或底板在两条竖直虚线之间温度基本相同,而竖直虚线外温度变化较大。以竖线外的北、南侧的顶板、底板的温度与其中心点温度之差为顶板、底板的北、南侧横向温差,具体见表2。
表 2 渡槽横向最大正(负)温差Table 2. Maximum transverse positive (negative) temperature difference of aqueduct单位:℃ 渡槽形式与位置 运行工况 顶板/底板位置 夏季最大正温差 冬季最大负温差 冬季最大正温差 有顶板渡槽顶板 通水 南侧端 12.6 −6.5 13.6 北侧端 7.9 −7.2 无 不通水 南侧端 4.7 −5.0 14.0 北侧端 1.0 −5.6 无 有顶板渡槽底板 通水 南侧端 18.5 −7.6 12.1 北侧端 11.7 −8.4 无 不通水 南侧端 9.7 −2.2 15.4 北侧端 3.4 −4.0 0.7 无顶板渡槽底板 通水 南侧端 17.7 −4.5 11.6 北侧端 12.0 −5.2 无 不通水 南侧端 1.6 无 15.2 北侧端 3.2 −2.1 4.4 从表2可见:无论顶板或底板,通水时的夏季最大正温差与冬季最大负温差绝对值均大于不通水时,且几乎所有南侧端温差绝对值大于北侧端温差绝对值;冬季南侧端正温差较大,在不通水时大于夏季最大正温差;有顶板渡槽的底板处温差最大,最大正温差为18.5 ℃,最大负温差为−8.4 ℃;无顶板渡槽底板最大正温差为17.7 ℃,最大负温差为−5.2 ℃。矩形渡槽顶板与底板的横向温差均较大,会产生较大的温度应力,设计中应给予考虑。
2.4 竖向温度梯度比较
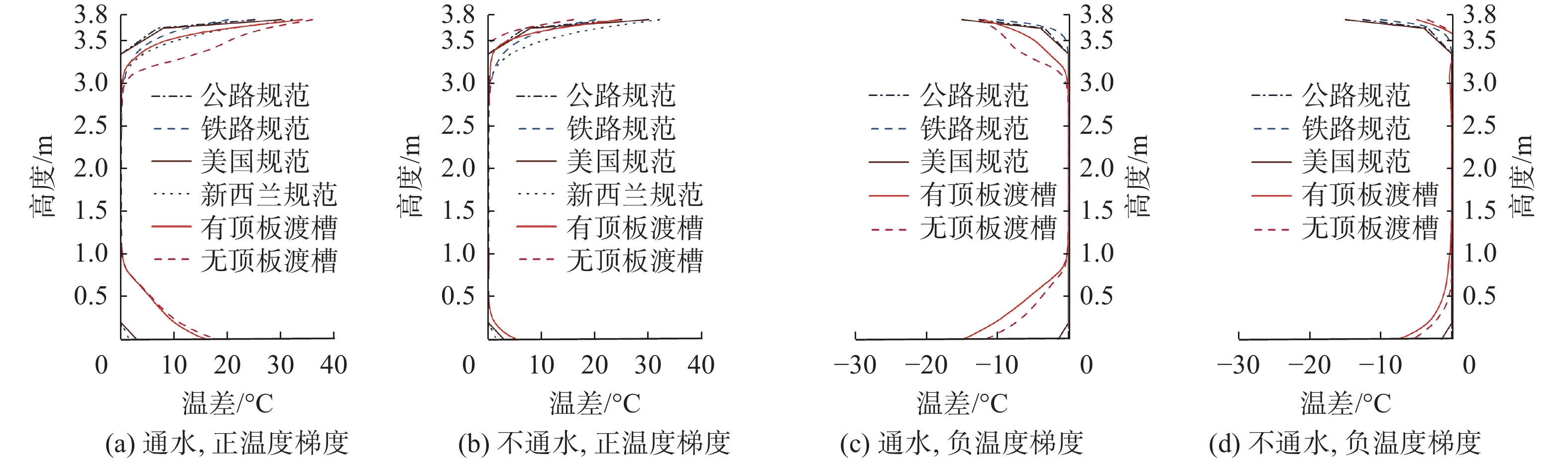
绘制渡槽的竖向温差最大时刻温度分布即竖向温度梯度见图7,并同国内外不同桥梁规范所推荐的竖向温度梯度模式进行比较。因桥梁箱涵一般都带有较长的悬臂,设计时可不考虑横向温度效应,各桥梁规范中关于横向温度梯度规定较少,故本文只进行渡槽竖向温度梯度与规范推荐对比。
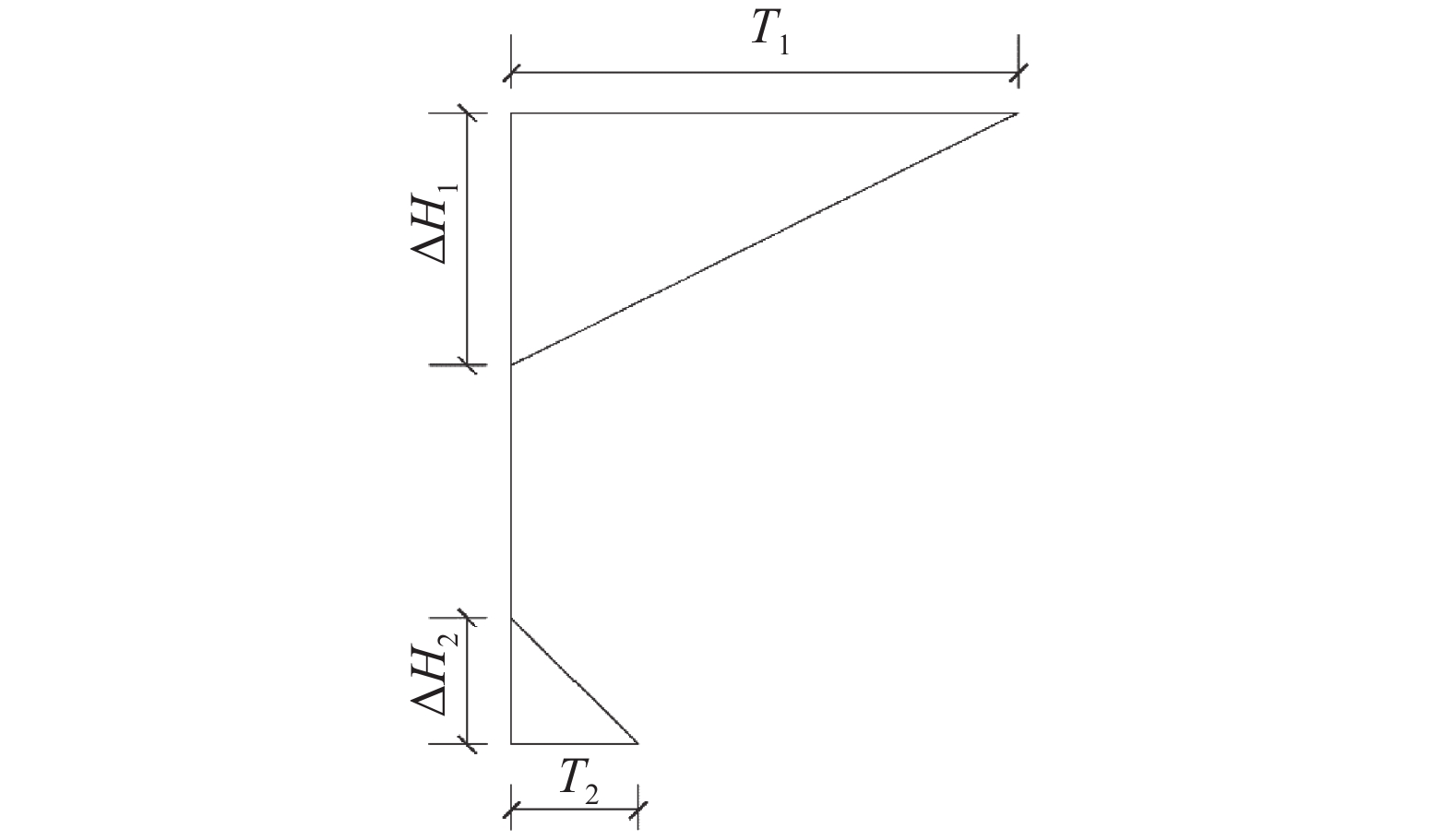
从图7可看出,渡槽的正、负温度梯度与各个桥梁规范[12, 21-23]中所推荐的形式大体相同。有顶板渡槽的顶板与腹板间正温度梯度曲线类似于抛物线,无顶板渡槽类似于直线;底板与腹板间温度梯度曲线均类似于抛物线。将本文计算值与规范推荐值进行比较,如表3所示,表中各参数代表含义见图8(图中T1和T2为温差,ΔH为距离)。
表 3 温度梯度特征值与各规范推荐值比较Table 3. Comparison of the characteristic values at the temperature gradient and the recommended values of each code温度梯度类型 通水与否 规范 温度梯度模式 T1/℃ T2/℃ ΔH1/m ΔH3/m 规范推荐正温度梯度 中国公路[12] 双折线 25 不考虑 0.4 不考虑 中国铁路[21] 幂函数 20 不考虑 1.1 不考虑 AASHTO[22] 双折线 30 3 0.4 0.2 新西兰[23] 抛物线 32 1.5 0.8 0.2 渡槽正温度梯度 通水 有顶板 33.9 16.3 0.80 1.05 无顶板 35.8 18.4 0.95 1.10 不通水 有顶板 24.5 5.5 1.00 0.50 无顶板 16.1 1.6 0.30 0.05 规范推荐负温度梯度 中国公路[12] 双折线 −12.5 不考虑 0.4 不考虑 中国铁路[21] 幂函数 −10 不考虑 0.35 不考虑 AASHTO[22] 双折线 −15 −3 0.4 0.2 新西兰[23] 抛物线 不考虑 不考虑 不考虑 不考虑 渡槽负温度梯度 通水 有顶板 −9.6 −11.5 0.75 1.10 无顶板 −8.2 −8.5 0.85 1.05 不通水 有顶板 −5.0 −7.8 0.20 1.25 无顶板 −3.4 −5.7 0.15 0.65 从表3可见,关于正温度梯度,在通水时有顶板渡槽与无顶板渡槽的T1和T2均大于所有规范推荐值。在不通水时有顶板渡槽的T1为24.5 ℃,与公路规范差异较小,T2为5.5 ℃,大于所有规范推荐值;无顶板渡槽T1为16.1 ℃,小于所有规范推荐值,T2为1.6 ℃,与新西兰规范推荐值相差较小。关于负温度梯度,在通水时有顶板渡槽T1为−9.6 ℃,小于我国公路规范推荐值,与铁路规范推荐值接近;无顶板渡槽T1为−8.5 ℃,小于我国公路与铁路规范推荐值。在不通水时有顶板渡槽与无顶板渡槽的T1小于所有规范推荐值。所有工况下T2均大于所有规范推荐值。
以上分析表明,渡槽在通水时无论有无顶板,所有桥梁规范推荐顶板处正温差值与计算值差异较大,中国公路规范推荐顶板处负温差值基本与计算值相符;所有桥梁规范推荐底板处正、负温差值与计算值相差较大。渡槽在不通水时我国桥梁规范推荐正温差值基本与有顶板渡槽计算值相符,与无顶板渡槽差异较大,所有规范推荐顶板负温差值和底板处正、负温差值与计算值相差较大。
3. 结 语
(1)渡槽在通水时的竖向最大正(负)温差远超不通水时的渡槽。在通水时夏季竖向最大正温差与冬季竖向最大负温差分别为35.8 ℃、−11.5 ℃;不通水时分别为24.5 ℃、−7.8 ℃。设计时应考虑竖向温度分布所带来的不利影响。
(2)渡槽的底板与顶板在夏季通水时的最大正温差与冬季通水时的最大负温差大于同期无水时的渡槽最大正(负)温差。渡槽的横向最大正温差为18.5 ℃,最大负温差为−8.4 ℃。较大的横向温度分布会产生较大的温度应力,设计中应给予考虑。
(3)渡槽竖向温度梯度与各种桥梁规范推荐的竖向温度梯度模式形式相似,但特征值存在较大差异,桥梁规范中的温度梯度模式不宜直接应用于渡槽。
-
表 1 渡槽最大竖向正(负)温差
Table 1 Maximum vertical positive (negative) temperature difference of aqueduct
单位:℃ 运行工况 渡槽形式 腹板位置 顶板 底板 夏季通水 有顶板渡槽 南侧腹板 30.5 15.2 北侧腹板 33.8 16.5 无顶板渡槽 南侧腹板 31.0 18.8 北侧腹板 35.8 18.7 夏季不通水 有顶板渡槽 南侧腹板 20.7 4.6 北侧腹板 24.5 5.5 无顶板渡槽 南侧腹板 16.1 4.9 北侧腹板 20.7 4.6 冬季通水 有顶板渡槽 南侧腹板 −9.0 −10.9 北侧腹板 −9.6 −11.5 无顶板渡槽 南侧腹板 −8.5 −7.7 北侧腹板 −8.6 −8.3 冬季不通水 有顶板渡槽 南侧腹板 −3.4 −5.7 北侧腹板 −4.9 −7.8 无顶板渡槽 南侧腹板 −3.8 −5.0 北侧腹板 −2.2 −7.6 表 2 渡槽横向最大正(负)温差
Table 2 Maximum transverse positive (negative) temperature difference of aqueduct
单位:℃ 渡槽形式与位置 运行工况 顶板/底板位置 夏季最大正温差 冬季最大负温差 冬季最大正温差 有顶板渡槽顶板 通水 南侧端 12.6 −6.5 13.6 北侧端 7.9 −7.2 无 不通水 南侧端 4.7 −5.0 14.0 北侧端 1.0 −5.6 无 有顶板渡槽底板 通水 南侧端 18.5 −7.6 12.1 北侧端 11.7 −8.4 无 不通水 南侧端 9.7 −2.2 15.4 北侧端 3.4 −4.0 0.7 无顶板渡槽底板 通水 南侧端 17.7 −4.5 11.6 北侧端 12.0 −5.2 无 不通水 南侧端 1.6 无 15.2 北侧端 3.2 −2.1 4.4 表 3 温度梯度特征值与各规范推荐值比较
Table 3 Comparison of the characteristic values at the temperature gradient and the recommended values of each code
温度梯度类型 通水与否 规范 温度梯度模式 T1/℃ T2/℃ ΔH1/m ΔH3/m 规范推荐正温度梯度 中国公路[12] 双折线 25 不考虑 0.4 不考虑 中国铁路[21] 幂函数 20 不考虑 1.1 不考虑 AASHTO[22] 双折线 30 3 0.4 0.2 新西兰[23] 抛物线 32 1.5 0.8 0.2 渡槽正温度梯度 通水 有顶板 33.9 16.3 0.80 1.05 无顶板 35.8 18.4 0.95 1.10 不通水 有顶板 24.5 5.5 1.00 0.50 无顶板 16.1 1.6 0.30 0.05 规范推荐负温度梯度 中国公路[12] 双折线 −12.5 不考虑 0.4 不考虑 中国铁路[21] 幂函数 −10 不考虑 0.35 不考虑 AASHTO[22] 双折线 −15 −3 0.4 0.2 新西兰[23] 抛物线 不考虑 不考虑 不考虑 不考虑 渡槽负温度梯度 通水 有顶板 −9.6 −11.5 0.75 1.10 无顶板 −8.2 −8.5 0.85 1.05 不通水 有顶板 −5.0 −7.8 0.20 1.25 无顶板 −3.4 −5.7 0.15 0.65 -
[1] 王铁梦. 工程结构裂缝控制[M]. 北京: 中国建筑工业出版社, 2017. WANG Tiemeng. Control of cracking in engineering structure [M]. Beijing: China Architecture & Building Press, 2017. (in Chinese)
[2] 佘安明, 水中和, 王树和. 干燥大温差条件下混凝土界面过渡区的研究[J]. 建筑材料学报,2008,11(4):485-488 doi: 10.3969/j.issn.1007-9629.2008.04.020 SHE Anming, SHUI Zhonghe, WANG Shuhe. Study on interfacial transition zone of concrete in dry climate and wide temperature change[J]. Journal of Building Materials, 2008, 11(4): 485-488. (in Chinese) doi: 10.3969/j.issn.1007-9629.2008.04.020
[3] 王长德, 冯晓波, 朱以文, 等. 水工渡槽的温度应力问题[J]. 武汉水利电力大学学报,1998,31(5):7-11 WANG Changde, FENG Xiaobo, ZHU Yiwen, et al. Research on thermal stress of aqueduct[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1998, 31(5): 7-11. (in Chinese)
[4] 王潘绣, 赵海涛, 黄冬辉. 暴雨降温作用下大型U型渡槽运行期温度场分析[J]. 水电能源科学,2010,28(9):79-81 doi: 10.3969/j.issn.1000-7709.2010.09.024 WANG Panxiu, ZHAO Haitao, HUANG Donghui. Temperature field analysis of large U-type aqueduct under action of storm cooling[J]. Water Resources and Power, 2010, 28(9): 79-81. (in Chinese) doi: 10.3969/j.issn.1000-7709.2010.09.024
[5] 赵山, 刘海涛, 吴泽玉. 寒潮作用下U形渡槽温度应力分析[J]. 人民长江,2009,40(17):62-63, 91 doi: 10.3969/j.issn.1001-4179.2009.17.021 ZHAO Shan, LIU Haitao, WU Zeyu. Analysis of temperature stress of U-shape aqueduct under cold wave action[J]. Yangtze River, 2009, 40(17): 62-63, 91. (in Chinese) doi: 10.3969/j.issn.1001-4179.2009.17.021
[6] 李书群, 和秀芬. 南水北调中线沼河渡槽运行期温度影响及对策[J]. 南水北调与水利科技,2006,4(3):22-24, 33 doi: 10.3969/j.issn.1672-1683.2006.03.007 LI Shuqun, HE Xiufen. Temperature influence and countermeasure in the minghe aqueduct in the middle route project of the south-to-north water transfer[J]. South-to-North Water Transfers and Water Science & Technology, 2006, 4(3): 22-24, 33. (in Chinese) doi: 10.3969/j.issn.1672-1683.2006.03.007
[7] 季日臣, 夏修身, 房振叶, 等. 预应力混凝土箱形渡槽日照温度应力分析[J]. 兰州交通大学学报,2006,25(1):8-11 doi: 10.3969/j.issn.1001-4373.2006.01.003 JI Richen, XIA Xiushen, FANG Zhenye, et al. Thermal stress analysis of concrete box aqueduct by solar radiation[J]. Journal of Lanzhou Jiaotong University, 2006, 25(1): 8-11. (in Chinese) doi: 10.3969/j.issn.1001-4373.2006.01.003
[8] ABID S R, TAYŞI N, ÖZAKÇA M. Experimental analysis of temperature gradients in concrete box-girders[J]. Construction and Building Materials, 2016, 106: 523-532. doi: 10.1016/j.conbuildmat.2015.12.144
[9] 张元海, 李乔. 预应力混凝土连续箱梁桥的温度应力分析[J]. 土木工程学报,2006,39(3):98-102 doi: 10.3321/j.issn:1000-131X.2006.03.015 ZHANG Yuanhai, LI Qiao. Analysis of thermal stress for prestressed concrete continuous box-girder bridges[J]. China Civil Engineering Journal, 2006, 39(3): 98-102. (in Chinese) doi: 10.3321/j.issn:1000-131X.2006.03.015
[10] 刘兴法. 预应力混凝土箱梁温度应力计算方法[J]. 土木工程学报,1986,19(1):44-54 LIU Xingfa. Computation of temperature stresses for prestressed concrete box girders[J]. China Civil Engineering Journal, 1986, 19(1): 44-54. (in Chinese)
[11] 彭友松. 混凝土桥梁结构日照温度效应理论及应用研究[D]. 成都: 西南交通大学, 2007. PENG Yousong. Studies on theory of solar radiation thermal effects on concrete bridges with application[D]. Chengdu: Southwest Jiaotong University, 2007. (in Chinese)
[12] 中华人民共和国交通运输部. 公路桥涵设计通用规范: JTG D60—2015[S]. 北京: 人民交通出版社, 2015. General specifications for design of highway bridges and culverts: JTG D60—2015[S]. Beijing: China Communications Press, 2015. (in Chinese)
[13] 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 1999. ZHU Bofang. Thermal stresses and temperature control of mass concrete[M]. Beijing: China Electric Power Press, 1999. (in Chinese)
[14] 刘江, 刘永健, 房建宏, 等. 高原高寒地区“上”形钢-混凝土组合梁的竖向温度梯度模式[J]. 交通运输工程学报,2017,17(4):32-44 doi: 10.3969/j.issn.1671-1637.2017.04.004 LIU Jiang, LIU Yongjian, FANG Jianhong, et al. Vertical temperature gradient patterns of 上-shaped steel-concrete composite girder in Arctic-alpine plateau region[J]. Journal of Traffic and Transportation Engineering, 2017, 17(4): 32-44. (in Chinese) doi: 10.3969/j.issn.1671-1637.2017.04.004
[15] 赵人达, 王永宝. 日照作用下混凝土箱梁温度场边界条件研究[J]. 中国公路学报,2016,29(7):52-61 doi: 10.3969/j.issn.1001-7372.2016.07.007 ZHAO Renda, WANG Yongbao. Studies on temperature field boundary conditions for concrete box-girder bridges under solar radiation[J]. China Journal of Highway and Transport, 2016, 29(7): 52-61. (in Chinese) doi: 10.3969/j.issn.1001-7372.2016.07.007
[16] 河南省水利勘测设计研究有限公司. 南水北调特大型渡槽关键技术研究与实践[M]. 北京: 中国水利水电出版社, 2018. Henan Water & Power Engineering Consulting Co., Ltd. Research and practice on key technologies of the South-to-North Water Diversion aqueduct[M]. Beijing: China Water Power Press, 2018. (in Chinese)
[17] 刘照球. 混凝土结构表面对流换热研究[D]. 上海: 同济大学, 2006. LIU Zhaoqiu. Research for convection heat transfer on the surface of concrete structure[D]. Shanghai: Tongji University, 2006. (in Chinese)
[18] 张锐. 自然环境下混凝土渡槽湿热效应分析研究[D]. 杨凌: 西北农林科技大学, 2020. ZHANG Rui. The moisture-heat coupling effect of aqueduct in natural environment[D]. Yangling: Northwest A & F University, 2020. (in Chinese)
[19] 李林, 周孝德, 宋策. 基于三维水温模型预测有支流影响下的水库水温[J]. 水土保持通报,2012,32(2):159-161 LI Lin, ZHOU Xiaode, SONG Ce. Prediction of temperature in a reservoir under influence of incoming branches based on 3D temperature model[J]. Bulletin of Soil and Water Conservation, 2012, 32(2): 159-161. (in Chinese)
[20] 张宁, 周鑫, 刘永健, 等. 基于点阵式测量的混凝土箱梁水化热温度场原位试验[J]. 土木工程学报,2019,52(3):76-86 ZHANG Ning, ZHOU Xin, LIU Yongjian, et al. In-situ test on hydration heat temperature of box girder based on array measurement[J]. China Civil Engineering Journal, 2019, 52(3): 76-86. (in Chinese)
[21] 国家铁路局. 铁路桥涵混凝土结构设计规范: TB 10092—2017[S]. 北京: 中国铁道出版社, 2017. National Railway Administration of the People’s Republic of China. Code for design of concrete structures of railway bridge and culvert: TB 10092—2017[S]. Beijing: China Railway Publishing House, 2017. (in Chinese)
[22] American Association of State Highway and Transportation Officials. AASHTO LRFD bridge construction specifications[S]. Washington, D C: American Association of State Highway and Transportation Officials, 2017.
[23] The NZ transport Agency. Bridge manual. Section 3: Design loading[S]. Wellington: Waka kotahi NZ transport Agency, 2013.
-
期刊类型引用(2)
1. 张延杰,曾显志,王海深,韩钟骐,邓开来,潘鹏. 高地震烈度区复杂地质条件渡槽结构. 清华大学学报(自然科学版). 2024(07): 1264-1277 .  百度学术
百度学术
2. 吴西杰,张龑,尹进步,何军龄,张曜. 采用贝叶斯理论的渡槽结构有限元模型更新方法. 水利水运工程学报. 2024(06): 148-156 .  本站查看
本站查看
其他类型引用(2)



 Email Alerts
Email Alerts RSS
RSS
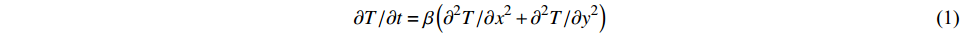
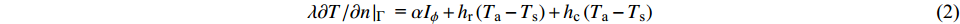
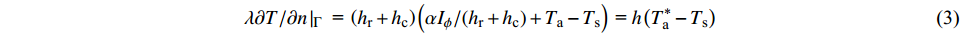
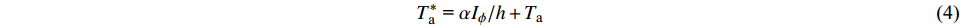

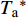
 下载:
下载: