Email Alerts
RSS
The investigation of local scouring of bridge group piers protected by quasi-stumps group
-
摘要:
为降低水流对并线桥墩周围河床的局部冲刷掏蚀，提出了一种放置于桥墩上游的拟树桩群防护结构，并分别通过模型试验和数值仿真的方法研究了拟树桩群布设距离、叶面积比和宽度对桥墩周围河床冲淤特性的影响。研究结果显示，数值计算结果与试验结果具有良好的吻合度。拟树桩群能够有效降低桥墩周围的流速，削弱水流的冲刷作用，并促进悬浮泥沙的沉积，有利于并线桥墩的稳定。有防护时的悬浮泥沙沉积量和河床泥沙冲刷量分别是无防护时的3.11倍和22%。拟树桩群的布设距离、叶面积比和宽度的增加会使悬浮泥沙的沉积量明显增加，但对河床泥沙冲刷量的影响较小。
Abstract:To mitigate the local scour erosion around parallel piers caused by water flow, a protective structure comprised of simulated quasi-stumps group placed upstream of the piers is proposed. The impact of the deployment distance (L), leaf area ratio (S), and width (W) of the simulated quasi-stumps group on the scour and deposition characteristics of the riverbed around the piers was investigated through both model experiments and numerical simulations. The results indicate a good agreement between the numerical calculations and experimental outcomes. The simulated quasi-stumps group can effectively reduce the flow velocity around the piers, mitigate the water scouring effect, and promote the deposition of suspended sediment, which is beneficial to the stability of the parallel piers. The deposition of suspended sediment and the amount of riverbed sediment scouring with protection are 3.11 times and 22% of those without protection, respectively. Increases in L, S, and W of the simulated quasi-stumps group significantly enhance the deposition of suspended sediment, but have a minor effect on riverbed sediment scour.
-
桥墩局部冲刷被认为是导致桥梁破坏的主要原因，根据Smith[1]对1847—1975年间143座发生重大事故桥梁的统计分析，其中70座桥梁的破坏是由洪水期间桥墩发生位移所引起；Lagasse等[2]的调查显示，大约60%的桥梁事故由冲刷造成。美国联邦公路局的调查结果表明，局部冲刷是桥梁设计和保护中需要首要考虑的问题之一[3]。根据冲刷防护机理，Chiew[4]将桥墩基础防护措施分为以下两类：一类用以降低来流中的下降水流和马蹄形漩涡对桥墩基础的冲刷能力；另一类用以提高桥墩周围河床的抗冲刷能力。Wang等[5]将这两类防护措施分别称为主动防护和被动防护。主动防护措施包括护圈防护[6]、桥墩开槽防护[7]、透水桩群防护[8]、环翼型防冲板防护[9]、螺纹桥墩防护[10]和下游分流板防护[11]等。被动防护措施包括抛石防护[12]、扩大基础防护[13]和四面体透水框架群防护[14]等。一些研究者发现明渠中植被的存在能有效降低其下游的流速[15]，促进水体中悬浮泥沙的沉降[16]，可将其应用于高含沙河流的桥墩局部冲刷防护。Abt等[17]研究了含植被水槽的泥沙沉积能力，结果表明植被能够使30%~70%的泥沙沉积，且泥沙淤积量主要与水流和植物叶片的长度有关；唐洪武等[18]在静水中设置了不同排列密度、不同直径的不锈钢细圆柱，测定了粒径为0.10~0.45 cm的泥沙沉降速度，研究发现在试验粒径范围内，含细圆柱静水中的泥沙沉速随细圆柱密度和泥沙粒径的增大而减小，并推导了考虑细圆柱密度和杆径的泥沙沉速公式。
模型试验是研究桥墩局部冲刷的主要手段，但由于其费用高和存在缩尺效应，并且近年来数值计算方法发展迅速，不少国内外学者对桥墩局部冲刷展开了数值模拟。Xiong等[19]提出并验证了一种考虑悬浮泥沙荷载的桥墩冲刷三维模型，可靠高效地模拟了桥墩周围泥沙输入和输出的动态平衡；熊文等[20]通过对计算流体力学软件ANSYS Fluent的二次开发，模拟了桥墩周围的动床冲刷过程，并将数值模拟结果与经典理论分析及部分试验结果进行对比，验证了该模拟计算方法的合理性与准确性；龙庆[21]利用FLOW 3D软件模拟了挟沙水流对桥墩局部冲刷的影响，结果显示相较于挟沙水流，清水下的局部冲刷深度更大，同时提出了一种用于计算挟沙水流下桥墩局部冲刷深度的经验公式；陈明等[22]利用FLOW 3D软件对刚性沉水植物的水力特性进行了数值模拟，从湍动能角度修改了希尔兹数，并对泥沙模块进行了改进，使FLOW 3D软件能更准确地模拟流场和泥沙运动，数值模拟得到的结果与试验数据吻合较好。此外，相比于单个桥墩，并线桥墩在桥梁中的运用越来越多，因此，许多学者通过试验和数值模拟研究了并线桥墩周围河床的局部冲刷，发现上游桥墩具有对下游桥墩的防护作用[23]，桥墩间水流呈现出明显的不连续和非线性，河床泥沙冲刷过程也变得更加复杂[24-28]。研究河道中并线桥墩周围的泥沙运动对实际工程更具有参考价值。
为降低桥墩周围的流速，阻滞推移质泥沙的运动，促进悬移质泥沙在桥墩周围的沉积，本文提出一种减小桥墩局部冲刷的拟树桩群结构，并采用物理模型试验和数值模拟的方法研究拟树桩群结构对桥墩周围河床冲刷的防护效果，分析其布设距离L、叶面积比S和宽度W对防护效果的影响，拟提出最佳防护效果组合。
1. 材料与方法
1.1 拟树桩群结构
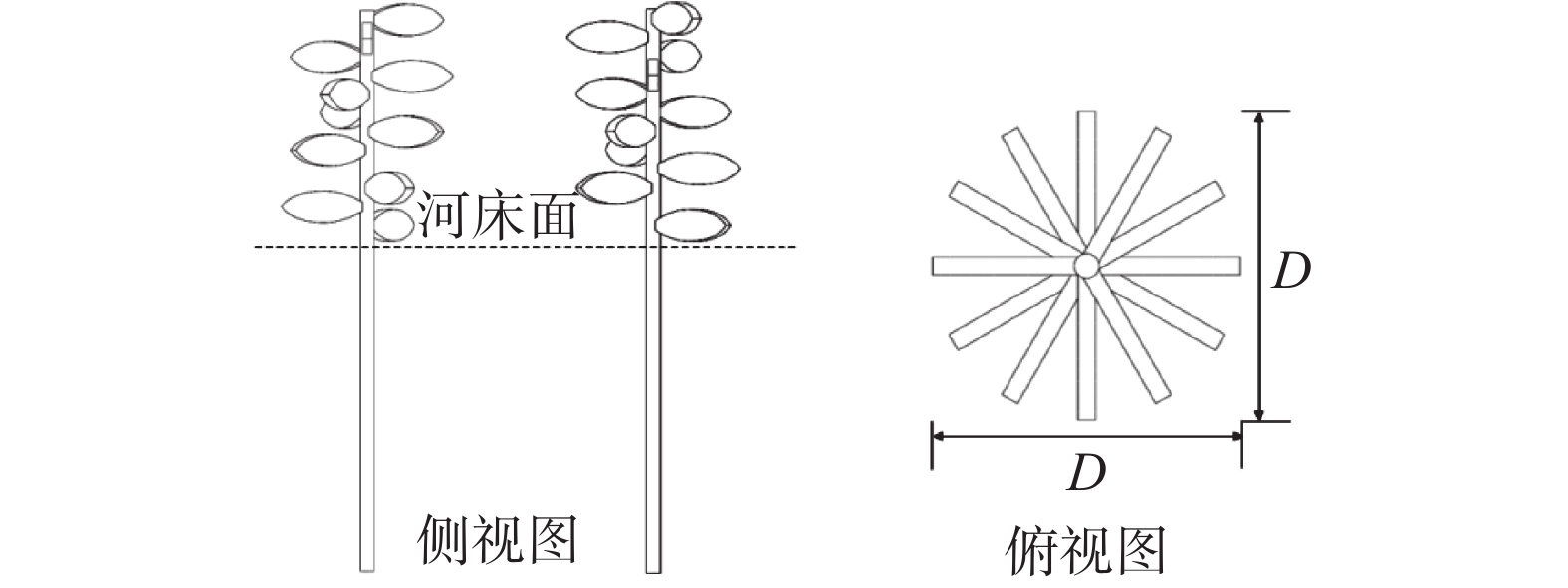
经多次调整后的拟树桩的结构见图1，桩群高于河床8 cm（1/3水深），沿水流方向每一列包含3个拟树桩，垂直于水流方向每一行包含3~7个拟树桩。每个拟树桩上有12片树叶，厚度均为3.6 mm，相邻叶片间的垂向间隔为6.7 mm。单个拟树桩的拆分结构如图2所示，以3片树叶为一组，共4组，第2组通过在第1组的基础上逆时针旋转30°得到，以此类推直至第4组，同一组内相邻叶片的夹角为120°，单个叶片的长和宽均为D。
1.2 模型试验
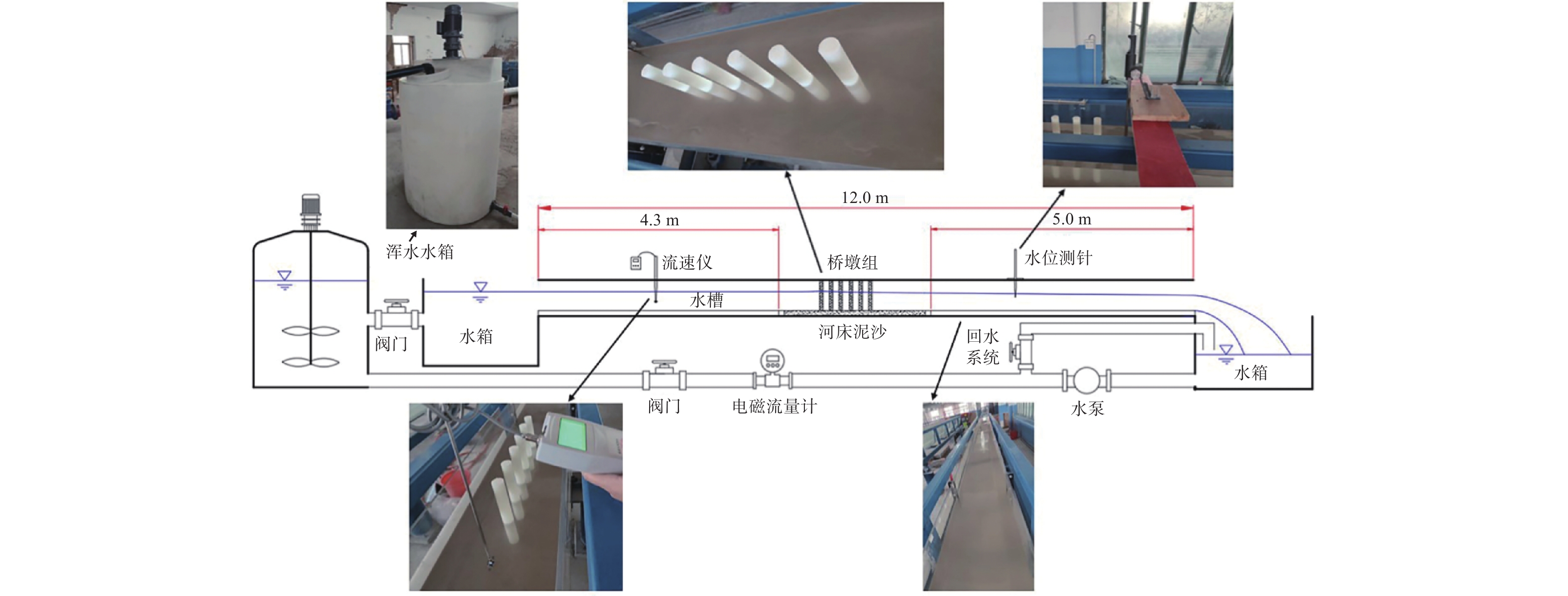
试验平台由矩形渠道、浑水水箱、供水水泵、电磁流量计、管道和阀门等部件组成，渠道尺寸为12 m×0.72 m×0.5 m（长×宽×高），如图3所示。通过控制水槽出水口的闸板开度调节水深，用针式水位计测量水深、冲刷深度和沉积高度，用LS300-A便携式流速测算仪测量流速。
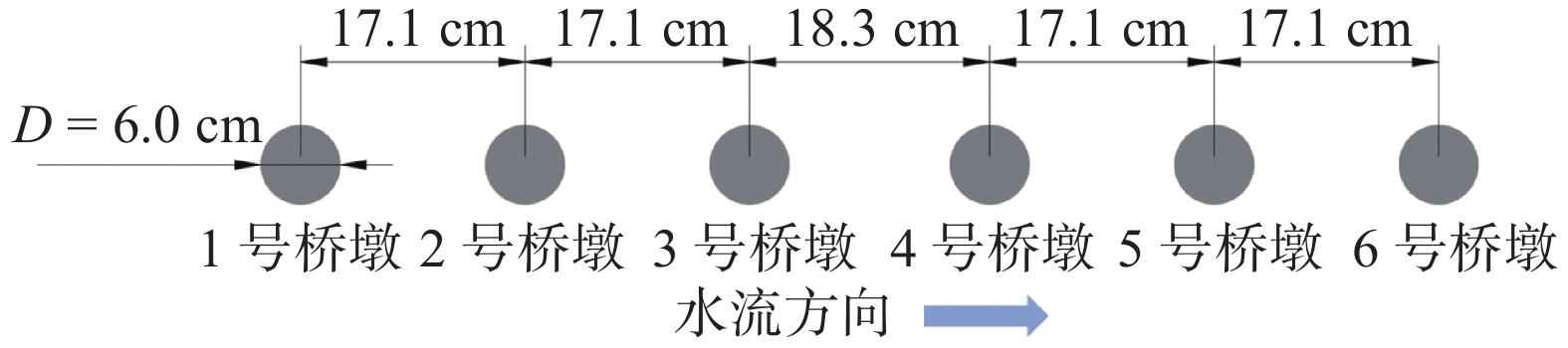
试验中所选用的桥墩结构为濮阳至湖北的阳新高速公路的黄河特大桥桥墩形式，桥墩直径为2 m，河道主槽平均流速为2.78 m/s，模型试验几何比尺为1∶33，流速比尺为1∶5.75，故试验桥墩直径为6 cm，流速为0.48 m/s。由于河道各处水深不相同，本文将河床面以上的水深设为4倍的桥墩直径即4D。进口水流中的含沙量为2.7 kg/m3，参考Debnath等[29]的研究，泥沙为粒径0.063 mm的均匀泥沙，泥沙休止角为30°。河床泥沙的中值粒径为0.34 mm，参考了Obied[30]的试验，粒径范围为0.15~0.41 mm，泥沙密度为2 650 kg/m3，泥沙休止角为32°。河床泥沙铺设厚度为10 cm。河床泥沙与进口水流中的泥沙均为非黏性沙，桥墩之间的相对位置及编号见图4。在每次试验开始前，先缓慢向水槽放水，使床料充水饱和并形成初始水深，防止初始冲刷影响试验结果。
1.3 数值模拟
1.3.1 控制方程及泥沙冲淤模型
对流体的计算包括质量守恒方程和动量守恒方程等，其控制方程是基于连续性方程和不可压缩黏性流体运动的Navier-Stokes方程。假设水为不可压缩流体，且使用笛卡尔坐标系，则质量守恒方程为：
$$ \frac{\partial}{\partial x}\left(uA_x\right)+\frac{\partial}{\partial y}\left(vA_y\right)+\frac{\partial}{\partial\text{z}}\left(wA_{\text{z}}\right)=\frac{R_{\rm{S}}}{\rho} $$ (1) 式中：$ \rho $为水的密度（kg/m3）；$ u $, $ v $, $ w $分别为$ x $, $ y $, ${\textit{z}} $方向的流速分量（m/s）；$ {A}_{x} $, $ {A}_{y} $, $ {A}_{\textit{z}} $分别为$ x $, $ y $, ${\textit{z}} $方向上可流动流体的面积分数；$ R_{\mathrm{S}} $为与物体运动相关的质量源项。
在3个方向上带有附加项的Navier-Stokes方程为：
$$ \frac{\partial u}{\partial t}+\frac{1}{V_{\mathrm{F}}}\left(uA_x\frac{\partial u}{\partial x}+vA_y\frac{\partial u}{\partial y}+wA_{\text{z}}\frac{\partial u}{\partial\text{z}}\right)=-\frac{1}{\rho}\frac{\partial p}{\partial x}+G_x+f_x-b_x-\frac{R_{\mathrm{S}\mathrm{ }}}{\rho V_{\mathrm{F}}}(u-u_{\rm{w}}-\delta u_{\rm{s}}) $$ (2) $$ \frac{\partial v}{\partial t}+\frac{1}{V_{\mathrm{F}}}\left(uA_x\frac{\partial v}{\partial x}+vA_y\frac{\partial v}{\partial y}+wA_{\text{z}}\frac{\partial v}{\partial\text{z}}\right)=-\frac{1}{\rho}\frac{\partial p}{\partial y}+G_y+f_y-b_y-\frac{R_{\mathrm{S}\mathrm{ }}}{\rho V_{\mathrm{F}}}(v-v_{\rm{w}}-\delta v_{\rm{s}}) $$ (3) $$ \frac{\partial w}{\partial t}+\frac{1}{V_{\mathrm{F}}}\left(uA_x\frac{\partial w}{\partial x}+vA_y\frac{\partial w}{\partial y}+wA_{\text{z}}\frac{\partial w}{\partial\text{z}}\right)=-\frac{1}{\rho}\frac{\partial p}{\partial\text{z}}+G_{\text{z}}+f_{\text{z}}-b_{\text{z}}-\frac{R_{\mathrm{S}\mathrm{ }}}{\rho V_{\mathrm{F}}}(w-w_{\rm{w}}-\delta w_{\rm{s}}) $$ (4) 式中：$ t $为时间（s）；$ p $为压强（Pa）；$ {V}_{\mathrm{F}} $为流动水体的体积分数；$ {G}_{x} $, $ {G}_{y} $, $ {G}_{\textit{z}} $分别为重力加速度在$ x $, $ y $, $ {\textit{z}} $方向的分量（m/s2），在本数值模拟中$ {G}_{x} $与$ {G}_{y} $均为零；$ {f}_{x} $, $ {f}_{y} $, $ {f}_{\textit{z}} $分别为$ x $, $ y $, $ {\textit{z}} $方向上的黏性加速度（m/s2），描述了物体在水体中改变速度或方向时由于水黏性力而产生的加速度；$ {b}_{x} $, $ {b}_{y} $, $ {b}_{\textit{z}} $分别为穿过多孔介质时在$ x $, $ y $, $ {\textit{z}} $方向上的流动损失；$ {u}_{\rm w} $, $ {v}_{\rm w} $, $ {w}_{\rm w} $为与流体运动速度相关的速度源项，用来表示外部输入或扰动源的速度；$ {u}_{\rm s} $, $ {v}_{\rm s} $, $ {w}_{\rm s} $为与运动物体相关的相对质量源表面的流体速度（m/s）；$ \delta $值的确定与源项类型有关，本文中$ \delta $=1。为了更准确地模拟水流和泥沙之间的相互作用，需要考虑水流和泥沙颗粒之间的相对运动，以及形状和速度分布，进口水流及其悬浮泥沙为源项。
泥沙冲淤模型中可以定义多种不同特性的非黏性泥沙，包括粒径、质量密度、临界切应力、拖曳系数、休止角、夹带系数和床载系数。泥沙有两种存在状态：悬浮和沉积，通过预测泥沙的侵蚀、平流和沉积来估计泥沙的运动。
本文数值计算采用基于Mastbergen和Van den Berg[31]的经验公式。临界希尔兹数采用Soulsby-Whitehouse公式[32]计算，首先需要计算无量纲参数$ {d}_{*} $：
$$ d_{\mathrm{*}}=d\left[\frac{\rho(\rho_{\rm{s}}-\rho) \left\| \mathbf{\mathbf{\mathit{g}}} \right\| }{\mu_{\rm{f}}^2}\right]^{1/3} $$ (5) 式中：$ d $为泥沙粒径(m)；$ {\rho }_{\rm s} $为泥沙密度（kg/m3）；$ \left\| \mathit{\mathbf{\mathbf{\mathit{g}}}} \right\| $为重力加速度$ g $的模；$ {\mu }_{\rm f} $为水的动态黏度（Pa·s）。
根据Soulsby-Whitehouse公式[32]计算无量纲临界希尔兹数$ {\theta }_{\rm cr} $：
$$ {\theta }_{\rm cr}=\frac{0.3}{1+1.2{d}_{*}}+0.055(1-\mathrm{e}\mathrm{x}\mathrm{p}(-0.02{d}_{*}\left)\right) $$ (6) 对位于斜坡上的泥沙颗粒的无量纲临界希尔兹数$ {\theta }_{\rm cr}^{{'}} $的计算如下[32]：
$$ {\theta }_{\rm cr}^{{'}}={\theta }_{\rm cr}\frac{\mathrm{cos}\alpha \mathrm{sin}\beta +\sqrt{{\mathrm{cos}}^{2}\beta {\mathrm{tan}}^{2}\phi -{\mathrm{sin}}^{2}\alpha {\mathrm{sin}}^{2}\beta }}{\mathrm{tan}\phi } $$ (7) 式中：$ \alpha $为水流流向与斜坡垂向之间的夹角；$ \beta $为河床倾斜角度；$ \phi $为泥沙休止角。
局部的临界希尔兹数计算如下：
$$ \theta =\frac{\tau }{\left\|{g}\right\|d({\rho }_{\rm s}-\rho )} $$ (8) 式中：$ \tau $为局部河床剪切应力（Pa）。
推移质变为悬移质时的泥沙挟带升力速度$ {{u}}_{\rm l} $的计算如下[31]：
$$ {u}_{\rm{l}}=\eta{n}_{\rm{s}}d_*^{0.3}(\theta-\theta_{\rm{c}r}^{'})^{1.5} \sqrt{ \left\| {g} \right\| d(\rho_{\rm{s}}-\rho)/\rho} $$ (9) 式中：$ \eta $为挟带系数；$ {{n}}_{\rm s} $为垂直于堆积泥沙表面的向外指向。
泥沙沉降采用Soulsby[32]提出的沉降速率方程：
$$ {u}_{\rm s}=\frac{{v}_{\rm f}}{d}\left[{\left(10.3{6}^{2}+1.049{d}_{*}^{3}\right)}^{0.5}-10.36\right] $$ (10) 式中：$ {u}_{\rm s} $为泥沙颗粒的沉降速率（m/s）；$ {v}_{\rm f} $为水的运动黏度（m2/s）。
假设沉降运动与重力方向相同，则沉降速度为：
$$ \mathit{u}_{\rm{s}}=u_{\rm{s}}\mathbf{\mathit{g}}/ \left\| \mathbf{\mathit{g}} \right\| $$ (11) 使用Meyer-Peter公式[33]计算推移质泥沙的无量纲输运率$ \varPhi $：
$$ \varPhi =\beta (\theta -{\theta }_{\rm cr}^{{'}}{)}^{1.5}{c}_{\rm b} $$ (12) 式中：$ \beta $为系数，通常取8.0；$ {c}_{\rm b} $为泥沙的体积分数。
床面单宽输沙率$ {q}_{\rm b} $的计算如下：
$$ {q}_{\rm b}=\varPhi {\left[\left\|{g}\right\|(({\rho -{\rho }_{\rm f}})/{{\rho }_{\rm f}}){d}^{3}\right]}^{0.5} $$ (13) 床面输运泥沙厚度$ \delta $的计算式为[34]：
$$ \frac{\delta }{d}=0.3{d}_{*}^{0.7}(({\theta }/{{\theta }_{\rm cr}^{{'}}})-1)^{0.5} $$ (14) 为计算每个网格内泥沙的运动，将$ q\mathrm{_b} $的值转换为推移质输沙速度$ {u}_{\rm b} $[34]:
$$ {u}_{\rm b}={{q}_{\rm b}}/{\delta {c}_{\rm b}{f}_{\rm b}} $$ (15) 式中：$ {f}_{\rm b} $为泥沙的临界填充率。
1.3.2 数值模型设置
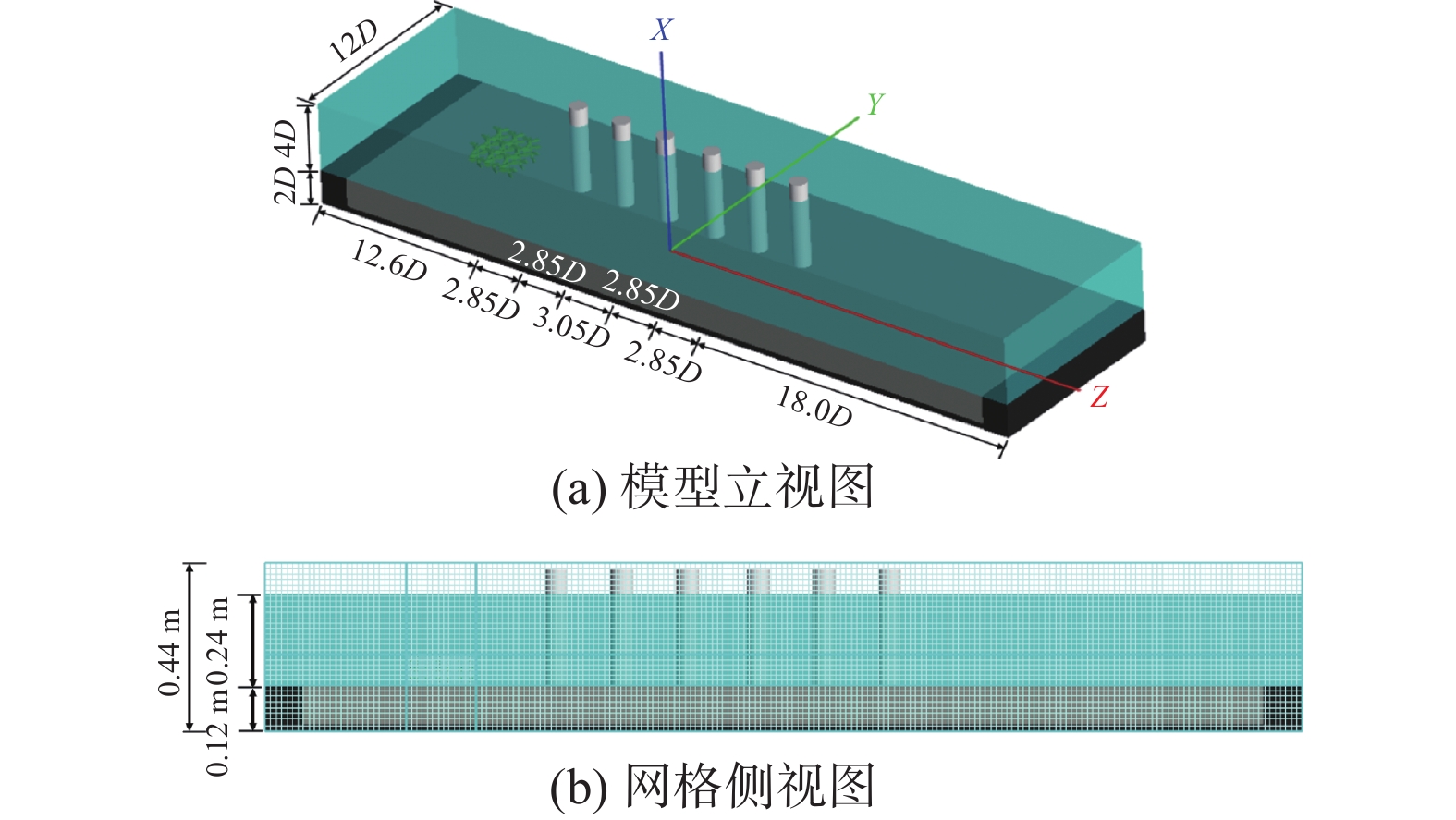
根据物理模型试验，设置数值模拟区域的长度为270 cm，宽度为72 cm（12D），高度为44 cm，1号桥墩与进水口之间的距离为76 cm（12.6D），6号桥墩与出水口之间的距离为108 cm（18D）(图5(a))。单个桥墩直径为6 cm，水深为24 cm（4D）。入口边界为速度，出口边界为自由出流，两侧和底部边界为壁面，顶部为相对压强为零的压力边界。此外，在试验段入口和出口放置了2个与河床同高的挡板，以防止初始冲刷。计算域采用结构化正交网格，主体网格尺寸为12.0 mm×12.0 mm×12.0 mm，拟树桩群区域的局部加密网格尺寸为3.6 mm×3.6 mm×3.6 mm，水面以上留有8 cm的空气区域，如图5(b)所示。模型的填充系数保持默认值0.64，河床泥沙的临界希尔兹数为0.061，夹带系数为0.018，床载系数为8.0；悬浮泥沙的临界希尔兹数为0.043，夹带系数为0.020，床载系数为9.3。数值仿真采用RNG k-ε湍流模型，采用Tru VOF方法追踪水流的自由表面。
1.3.3 网格尺寸无关性验证
E0工况的网格尺寸无关性分析如表1所示，dm和da分别表示最大冲刷深度和平均冲刷深度（冲刷坑内10个测点的均值）。结果显示，当网格尺寸减小到0.012 m时，误差趋于稳定，且均小于5%，当网格尺寸减小到0.010 m时，平均误差仅下降了0.3%，从计算效率角度出发，选择0.012 m为本数值模拟的最优网格尺寸。
表 1 网格尺寸无关性分析Table 1. Analysis of mesh size independence网格尺寸/m 网格数量 数值模拟 模型试验 平均误差/% dm/m da/m dm/m da/m 0.016 249 151 0.017 8 0.015 3 0.015 9 0.013 4 13.1 0.014 351 394 0.017 1 0.014 5 7.9 0.012 562 964 0.016 6 0.014 1 4.8 0.010 946 020 0.016 6 0.014 0 4.5 1.4 试验变量及工况
试验设置了3个变量、共14组工况，如表2所示，V为入口平均流速（所有工况都为0.48 m/s），H为水深（所有工况都为0.24 m），L为拟树桩群下游边与1号桥墩上游顶点之间的水平距离（布设距离），W为拟树桩群的宽度（宽度），S为拟树桩上单个叶片面积与单个桥墩横截面面积之比（叶面积比）。
表 2 试验工况Table 2. Experimental conditions工况 L W S 工况 L W S E0 无拟树桩群防护 E7 3D 5D 0.088 E1 D 3D 0.088 E8 3D 6D 0.088 E2 2D 3D 0.088 E9 3D 7D 0.088 E3 3D 3D 0.088 E10 D 3D 0.103 E4 4D 3D 0.088 E11 D 3D 0.118 E5 5D 3D 0.088 E12 D 3D 0.133 E6 3D 4D 0.088 E13 D 3D 0.148 为了确定试验时长，对E0工况进行了预试验和数值模拟。试验结果显示， 试验开始后1 h的最大冲刷深度达到了最大值的96.4%；模拟结果显示，1 h的最大冲刷深度和冲刷面积分别达到了最大值的97.1%和96.0%，1 h后的冲刷增幅已经非常小，故将试验持续时间和模拟时长设置为1 h。
2. 数值仿真验证
为了验证模拟的准确性，对不同工况下桥墩周围流速进行分析，流速测点如图6所示，所有点均位于距河床面1/4水深处。
选取E0和E5工况进行验证，不同位置处试验和数值计算流速如表3所示。结果显示，模拟和试验流速的最大相对误差为8.58%，说明模拟流场与试验流场吻合较好。
表 3 E0和E5工况下试验和模拟的流速及相对误差Table 3. Flow velocities and relative errors under conditions E0 and E5 in experiments and simulations测点 E0工况 E5工况 试验流速/(m/s) 模拟流速/(m/s) 相对误差/% 试验流速/(m/s) 模拟流速/(m/s) 相对误差/% A 0.351 0.332 −5.42 0.233 0.253 8.58 B 0.443 0.417 −5.87 0.336 0.350 4.17 C 0.147 0.144 −2.04 0.121 0.123 1.65 D 0.253 0.254 0.40 0.205 0.206 0.49 选取E3工况对比试验和数值仿真河床结构变化，结果（图7）显示，模拟与试验的沉积区域大致相同，淤积主要集中在拟树桩群与第1个桥墩之间及并线桥墩中轴线上，前者近似呈梯形状，后者呈一条直线，最大淤积高度的误差仅为5.7%。
![]()
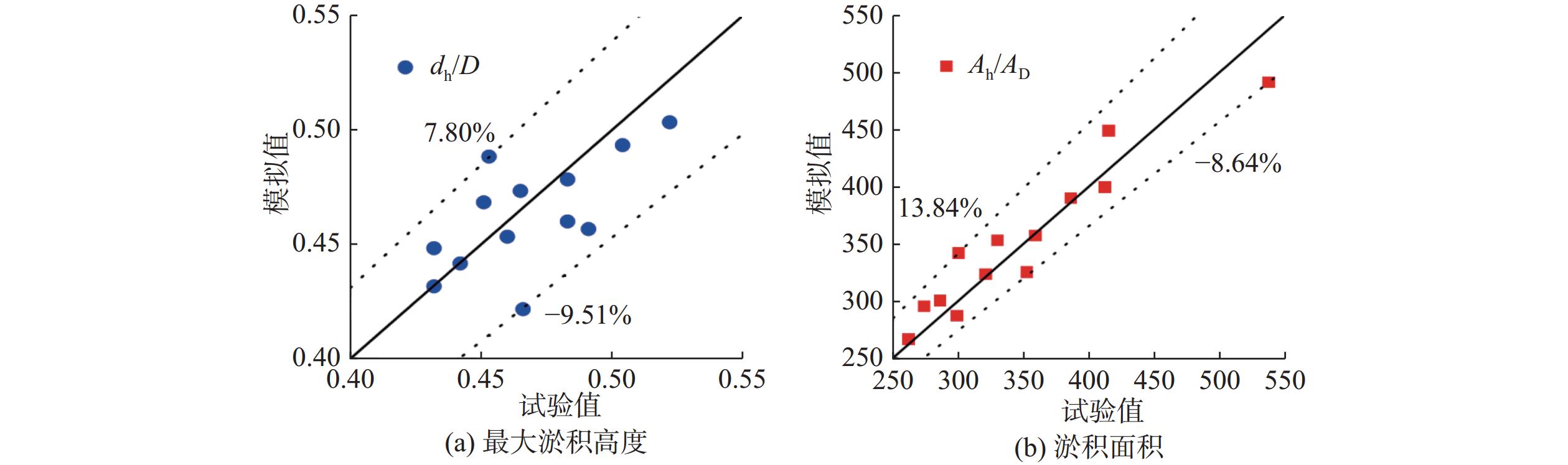
图 7 模拟和试验淤积后的河床对比Figure 7. Comparison of riverbed accretion in simulation and experiment为进一步验证模拟结果的准确性，对淤积高度、淤积面积等指标进行分析对比，本研究中，当淤积高度超过1 mm的区域为淤积区域，当冲刷深度超过1 mm的区域为冲刷区域。淤积高度、淤积面积无量纲式为：Hde=dh/D，Ade=Ah/AD，其中：Hde为无量纲最大淤积高度；Ade为无量纲淤积面积；dh为最大淤积高度；Ah为淤积面积；AD为单个桥墩的横截面面积。E1至E13工况的试验与模拟结果对比如图8所示。可见，Hde试验值与模拟值相对偏差为−9.51%~7.80%，Ade的相对偏差为−8.64%~13.84%。这说明数值模拟结果与试验结果吻合较好。
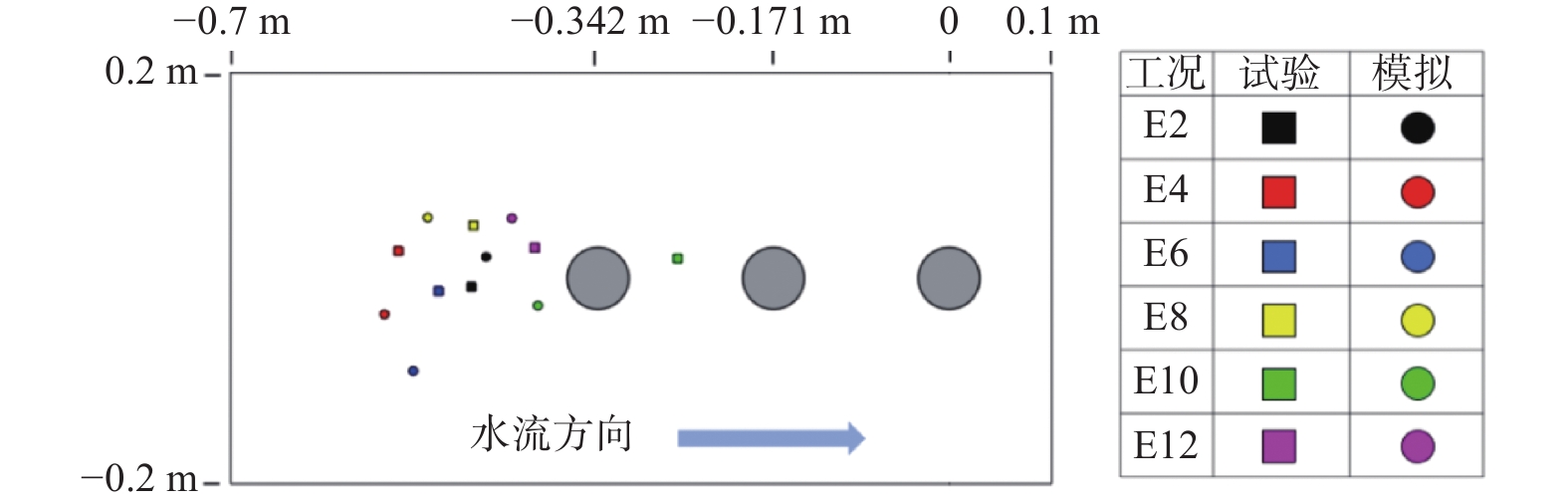
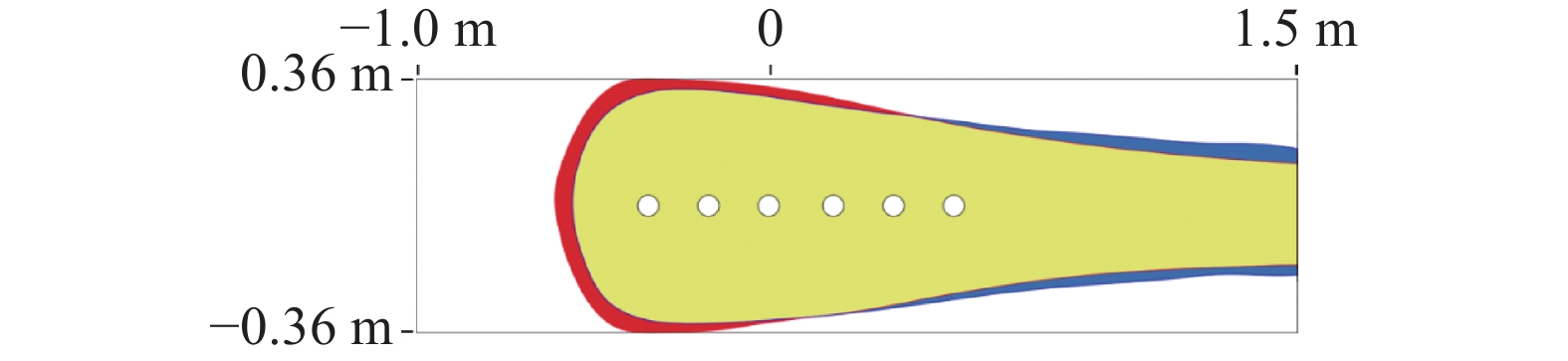
选择E2、E4、E6、E8、E10和E12工况，比较试验和模拟中产生最大沉积高度的位置，其空间分布如图9所示。结果显示，试验和模拟中最高沉积点之间的平均距离为6.70 cm（1.12D），一致性较好。E11工况下的沉积区域分布如图10所示。图10中黄色为模拟与试验重叠的沉积区域，红色和蓝色分别代表数值模拟和试验中沉积的区域。
![]()
图 9 试验和模拟产生最大沉积高度的对比Figure 9. Comparison of maximum deposition height in experiments and simulations![]()
图 10 试验和模拟中沉积区域分布的对比Figure 10. Comparison of deposition area distribution in experiments and simulations3. 结果分析
3.1 防护效果分析
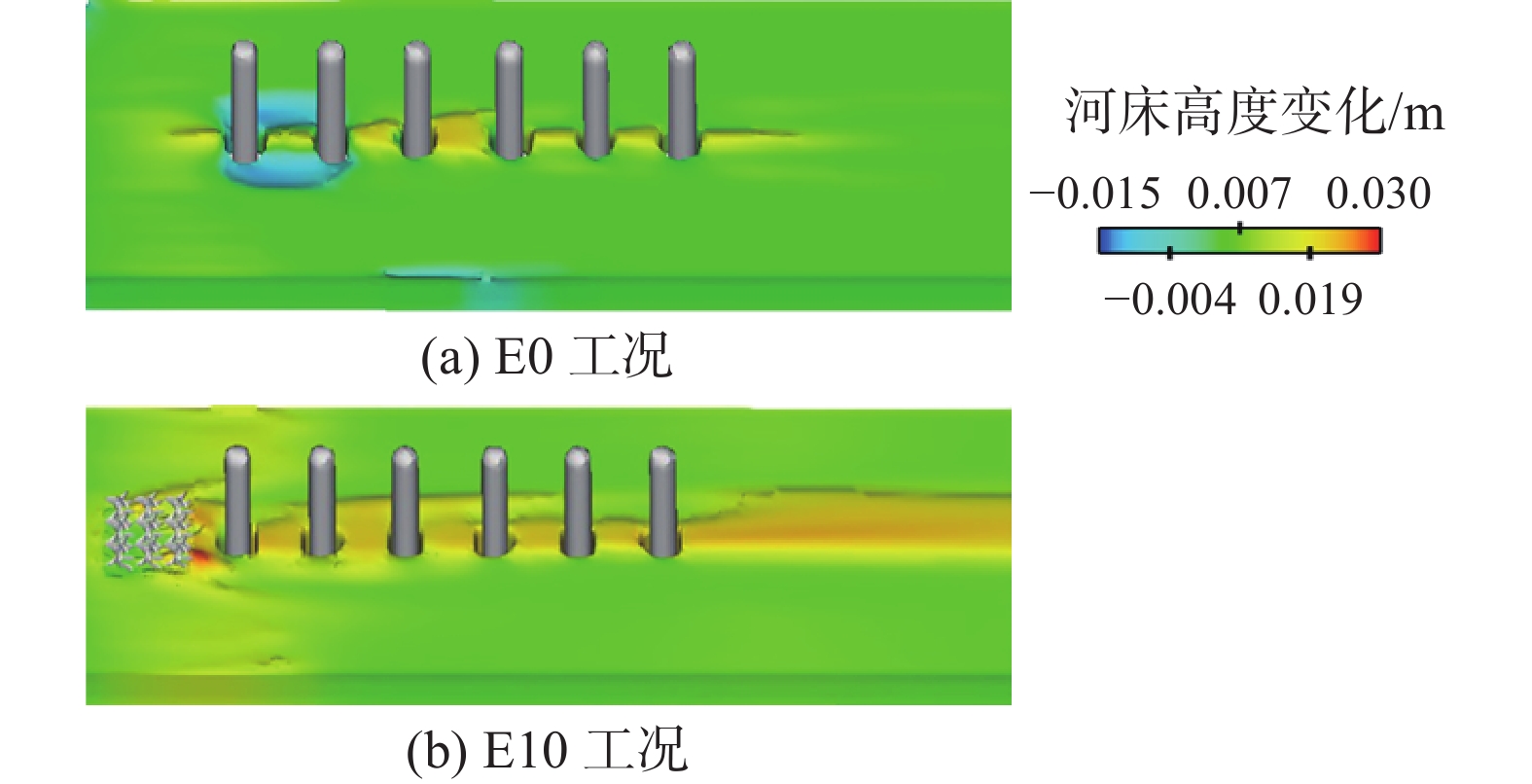
图11为无防护（E0工况）和有防护（E10工况）时的河床冲淤模拟结果。从图11可以看出，在无拟树桩群防护的情况下，上游第1个和第2个桥墩周围河床出现冲刷，设置拟树桩群防护后，冲刷得到有效遏制且形成淤积，并且桥墩中轴线附近淤积加剧。这表明拟树桩群对并线桥墩的局部冲刷具有显著的防护效果。
![]()
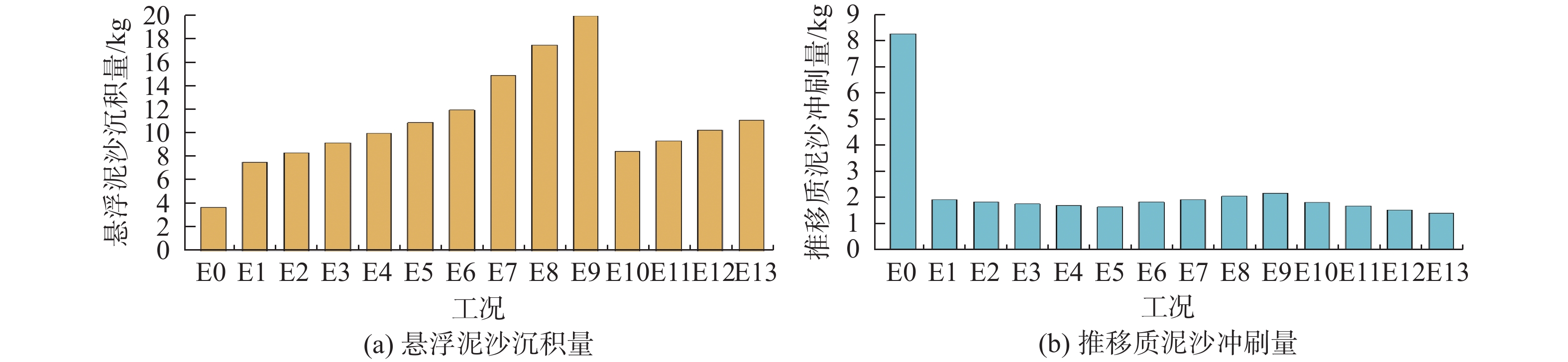
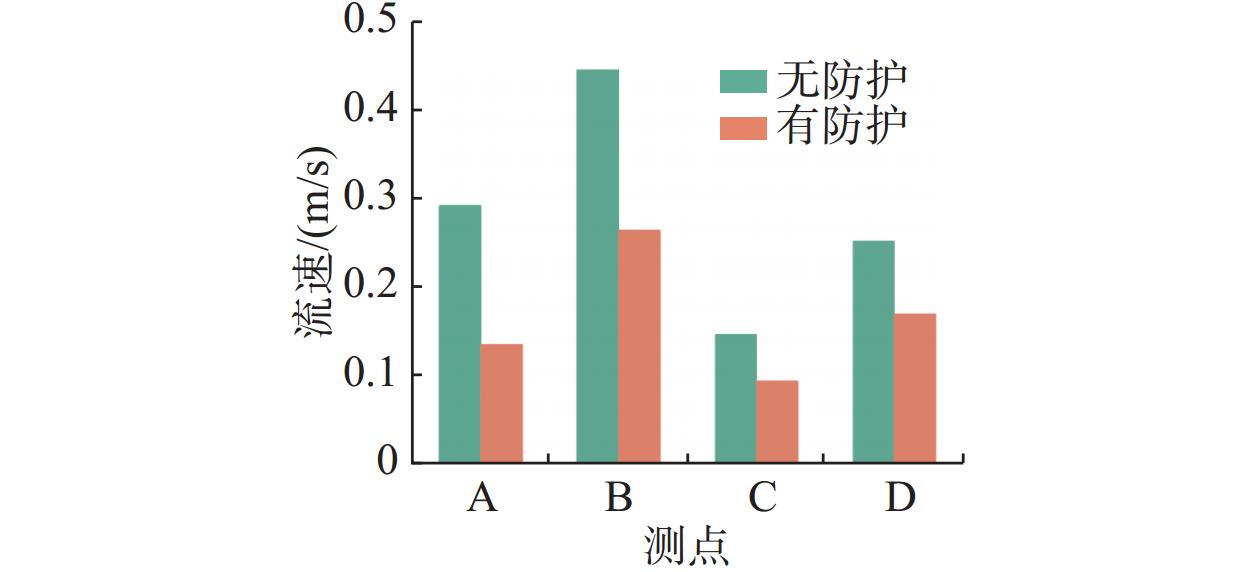
图 11 有无拟树桩群防护时的河床冲淤对比Figure 11. Comparison of scour and deposition with and without the protection of quasi-stumps group为进一步分析拟树桩群防护对悬移质和推移质的影响，对无防护和有防护时的悬浮泥沙沉积量和推移质泥沙冲刷量进行研究（如图12所示）。结果显示，E0工况下的悬浮泥沙沉积量为3.69 kg，E1至E13工况下的悬浮泥沙平均沉积量为11.46 kg，表明拟树桩群促进悬浮泥沙沉积的效果显著。E0工况下的推移质泥沙冲刷量为8.25 kg，E1至E13工况下的推移质泥沙平均冲刷量为1.78 kg，这表明拟树桩群能有效削弱水流对河床的冲刷作用。桥墩周围的流速分布是河床冲淤的主要因素，通过对比E0及E1至E13的流速分布（如图13）可知，在拟树桩群防护下桥墩周围的流速明显降低，有利于悬移质泥沙的沉积。
![]()
图 12 各工况下的悬浮泥沙沉积量和推移质泥沙冲刷量Figure 12. Amount of suspended sediment deposition and the bed-load sediment scour under various conditions![]()
图 13 不同测点流速对比Figure 13. Comparison of flow velocities at different measurement points3.2 拟树桩群布置参数对淤积特性的影响
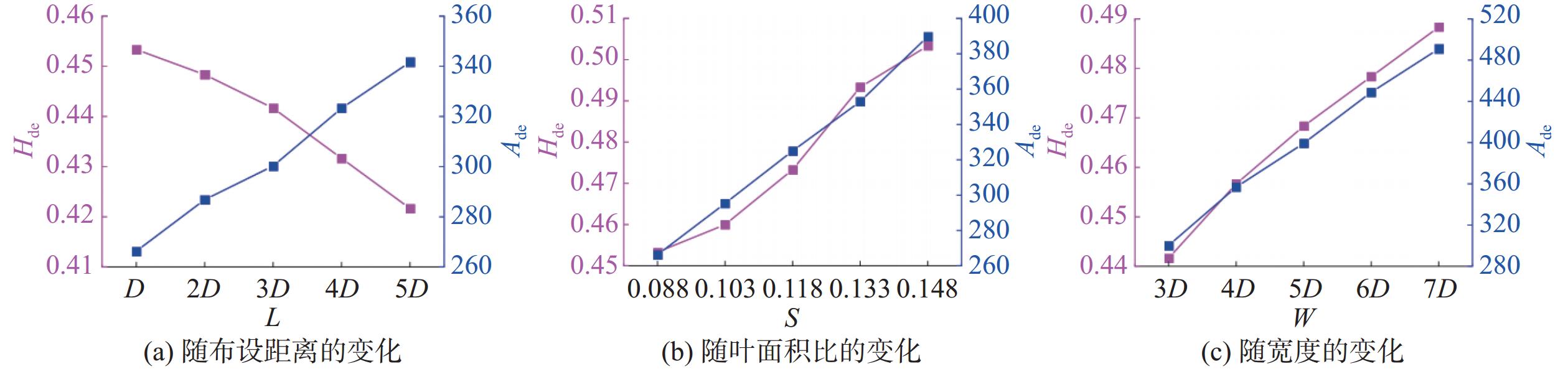
图14为无量纲最大淤积高度Hde和淤积面积Ade随布设参数的变化。从图14可以看出，随着布设间距L的增加，淤积高度逐渐减小，淤积面积逐渐增大；叶面积比S和宽度W对Hde和Ade的影响规律相似，随着S和W的增大，Hde和Ade均呈现增大趋势，而宽度W对淤积面积的影响更为显著。这是因为W越大，被拟树桩群减速的流体区域越大，进而导致更多的悬浮泥沙沉积，淤积面积增大明显。
![]()
图 14 无量纲最大淤积高度和淤积面积随拟树桩群布设参数的变化Figure 14. Variation of dimensionless maximum deposition height and deposition area with simulated quasi-stumps group parameters3.3 布置参数对输沙量的影响
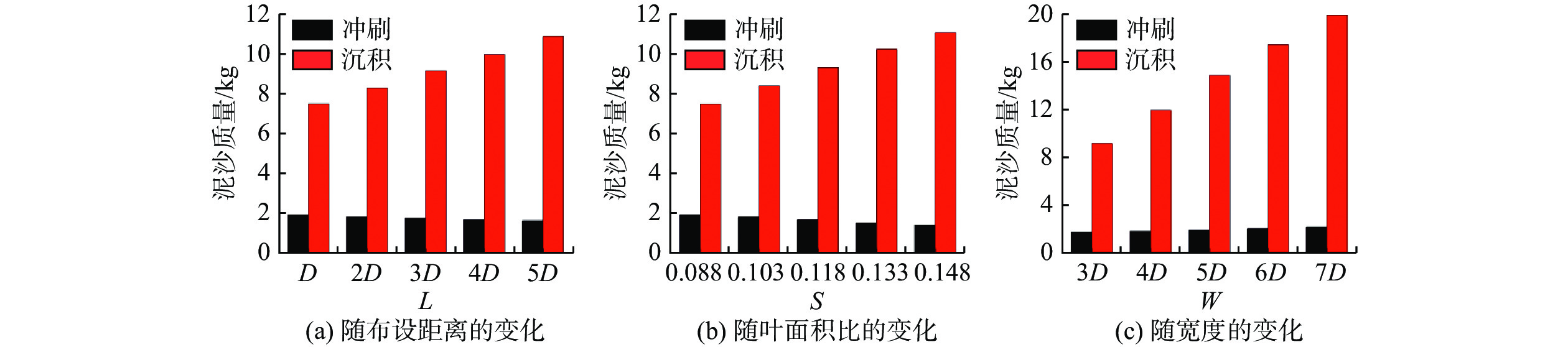
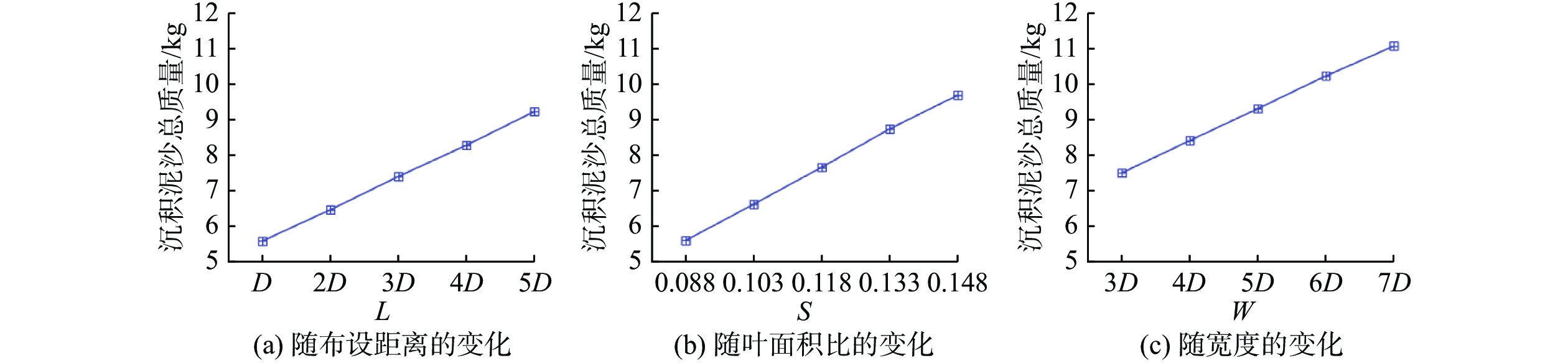
悬浮泥沙沉积量和河床泥沙冲刷量随布设参数的变化如图15所示。可见，随着L的增大，悬浮泥沙的沉积量逐渐增加，河床泥沙的冲刷量逐渐减少。随着S的增加，泥沙沉积量逐渐增加，冲刷量逐渐降低。随着W的增大，悬浮泥沙沉积量和河床泥沙冲刷量均逐渐增加。拟树桩群的宽度对悬浮泥沙沉积的影响最显著，并且悬浮泥沙的沉积量远大于河床泥沙的冲刷量。另外，河床上的泥沙总质量均随L、S和W的增加而增加（图16）。
![]()
图 15 河床泥沙冲刷量和悬浮泥沙沉积量随布设参数的变化Figure 15. Variation of riverbed sediment scour quantity and suspended sediment deposition quantity with layout parameters![]()
图 16 河床上泥沙总质量随布设参数的变化Figure 16. Variation of the total sediment mass on the riverbed with layout parameters3.4 布置参数对并线桥墩中轴线淤积高度的影响
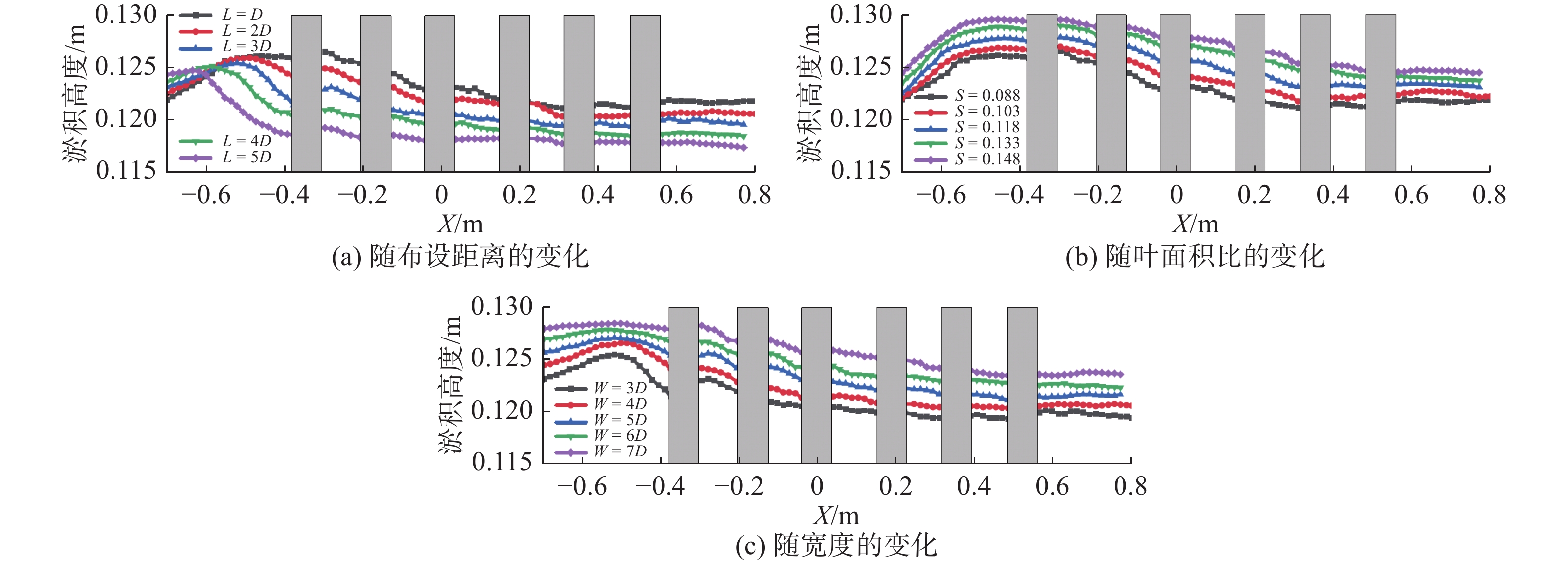
不同布置参数下，桥墩中轴线位置河床冲淤高度变化如图17所示。可见，桥墩上下游的淤积高度随着布设距离L的增加而降低、随着叶面积比S和宽度W的增加而增加。即L越小、S和W越大，拟树桩群的防护效果越好，这与泥沙沉积量随着S和W的增加而增加的变化规律一致，但与泥沙沉积量随L的变化规律相反，这是因为L越大，拟树桩群距离水流入口越近，能使更多的悬浮泥沙沉积在整个河床上，但同时其距离桥墩越远，对桥墩周围河床的防护效果越差。
![]()
图 17 沿并线桥墩中轴线的河床淤积高度随布设参数的变化Figure 17. Variation of the siltation height of riverbed along the centerline of the group piers with layout parameters3.5 布置参数对桥墩周围流速的影响
不同布置参数下各测点流速变化如图18所示。结果表明，随着L的增大，各测点流速均呈增大趋势，其中测点A流速增幅最大；随S的增大，各点流速均逐渐减小，其中A点的变化最为显著，C和D点的变化最小；随W的增加，各点的流速均减小，其中B点的变化最大，A、C、D三点的变化程度基本一致。这是因为W从3D增加到7D的过程中，A、C、D三点始终处于被拟树桩群减速的流体区域内，而B点经历了从处在减速区边缘到处于减速区内的过程。
![]()
图 18 桥墩周围不同测点流速随布设参数的变化Figure 18. Variation of flow velocities at different points around the piers group with layout parameters结合图14和图15可知：随着L的增加，桥墩周围流速增大的同时，河床上的淤积面积和悬浮泥沙沉积量不减反增，造成这种结果的主要原因是L越大，下游受拟树桩群影响造成的流速降低的区域越大，更有利于悬浮泥沙的沉积和淤积面积的增加；随着S和W的增加，桥墩周围的流速逐渐减小，最大淤积高度、淤积面积和悬浮泥沙沉积量均逐渐增加。
4. 结 语
本文采用试验与数值模拟相结合的方法研究了拟树桩群对桥墩局部冲刷的防护效果，同时分析了其布设距离L、叶面积比S和宽度W对桥墩周围泥沙淤积特性的影响。结果表明：数值模拟所得到的结果与试验结果吻合较好；拟树桩群防护不仅有利于悬浮泥沙沉积，还可有效降低桥墩周围河床的泥沙掏蚀现象；L、S和W的变化对河床泥沙冲刷量的影响较小，但对悬浮泥沙的沉积量具有较大的影响，且悬浮泥沙沉积量随L、S和W的增加而增加。根据并线桥墩中轴线上的淤积高度随L、S、W的变化结果可知，在流速为0.48 m/s、含沙量为2.7 kg/m3的条件下，防护效果最优的拟树桩群组合为：L=D，S=0.148，W=7D。
-
![]()
图 7 模拟和试验淤积后的河床对比
Figure 7. Comparison of riverbed accretion in simulation and experiment
![]()
图 9 试验和模拟产生最大沉积高度的对比
Figure 9. Comparison of maximum deposition height in experiments and simulations
![]()
图 10 试验和模拟中沉积区域分布的对比
Figure 10. Comparison of deposition area distribution in experiments and simulations
![]()
图 11 有无拟树桩群防护时的河床冲淤对比
Figure 11. Comparison of scour and deposition with and without the protection of quasi-stumps group
![]()
图 12 各工况下的悬浮泥沙沉积量和推移质泥沙冲刷量
Figure 12. Amount of suspended sediment deposition and the bed-load sediment scour under various conditions
![]()
图 13 不同测点流速对比
Figure 13. Comparison of flow velocities at different measurement points
![]()
图 14 无量纲最大淤积高度和淤积面积随拟树桩群布设参数的变化
Figure 14. Variation of dimensionless maximum deposition height and deposition area with simulated quasi-stumps group parameters
![]()
图 15 河床泥沙冲刷量和悬浮泥沙沉积量随布设参数的变化
Figure 15. Variation of riverbed sediment scour quantity and suspended sediment deposition quantity with layout parameters
![]()
图 16 河床上泥沙总质量随布设参数的变化
Figure 16. Variation of the total sediment mass on the riverbed with layout parameters
![]()
图 17 沿并线桥墩中轴线的河床淤积高度随布设参数的变化
Figure 17. Variation of the siltation height of riverbed along the centerline of the group piers with layout parameters
![]()
图 18 桥墩周围不同测点流速随布设参数的变化
Figure 18. Variation of flow velocities at different points around the piers group with layout parameters
表 1 网格尺寸无关性分析
Table 1 Analysis of mesh size independence
网格尺寸/m 网格数量 数值模拟 模型试验 平均误差/% dm/m da/m dm/m da/m 0.016 249 151 0.017 8 0.015 3 0.015 9 0.013 4 13.1 0.014 351 394 0.017 1 0.014 5 7.9 0.012 562 964 0.016 6 0.014 1 4.8 0.010 946 020 0.016 6 0.014 0 4.5 
下载: 导出CSV
表 2 试验工况
Table 2 Experimental conditions
工况 L W S 工况 L W S E0 无拟树桩群防护 E7 3D 5D 0.088 E1 D 3D 0.088 E8 3D 6D 0.088 E2 2D 3D 0.088 E9 3D 7D 0.088 E3 3D 3D 0.088 E10 D 3D 0.103 E4 4D 3D 0.088 E11 D 3D 0.118 E5 5D 3D 0.088 E12 D 3D 0.133 E6 3D 4D 0.088 E13 D 3D 0.148
下载: 导出CSV
表 3 E0和E5工况下试验和模拟的流速及相对误差
Table 3 Flow velocities and relative errors under conditions E0 and E5 in experiments and simulations
测点 E0工况 E5工况 试验流速/(m/s) 模拟流速/(m/s) 相对误差/% 试验流速/(m/s) 模拟流速/(m/s) 相对误差/% A 0.351 0.332 −5.42 0.233 0.253 8.58 B 0.443 0.417 −5.87 0.336 0.350 4.17 C 0.147 0.144 −2.04 0.121 0.123 1.65 D 0.253 0.254 0.40 0.205 0.206 0.49
下载: 导出CSV
-
[1] SMITH D W. Why do bridges fail[J]. Civil Engineering, 1977, 47: 58-62.
[2] LAGASSE P F, CLOPPER P E, ZEVENBERGEN L W, et al. NCHRP Report 593: Countermeasures to protect bridge piers from scour[R]. Washington: Transportation Research Board, 2007.
[3] ARNESON L A, ZEVENBERGEN L W, LAGASSE P F, et al. Evaluating scour at bridges[M]. 5th Ed. Washington: Federal Highway Administration, 2012.
[4] CHIEW Y M. Scour protection at bridge piers[J]. Journal of Hydraulic Engineering, 1992, 118(9): 1260-1269. doi: 10.1061/(ASCE)0733-9429(1992)118:9(1260)
[5] WANG C, YU X, LIANG F Y. A review of bridge scour: mechanism, estimation, monitoring and countermeasures[J]. Natural Hazards, 2017, 87(3): 1881-1906. doi: 10.1007/s11069-017-2842-2
[6] OSROUSH M, HOSSEINI S A, KAMANBEDAST A A. Countermeasures against local scouring around bridge abutments: combined system of collar and slot[J]. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 2021, 45(1): 11-25. doi: 10.1007/s40996-020-00443-4
[7] 牟献友, 乔春林, 冀鸿兰, 等. 桥墩上环翼型防冲板和开缝组合新型防护试验研究[J]. 水力发电学报,2017,36(4):26-37. (MOU Xianyou, QIAO Chunlin, JI Honglan, et al. Experimental study on anti-scour devices of slotted bridge piers with a semicircular fin[J]. Journal of Hydroelectric Engineering, 2017, 36(4): 26-37. (in Chinese) doi: 10.11660/slfdxb.20170404 MOU Xianyou, QIAO Chunlin, JI Honglan, et al. Experimental study on anti-scour devices of slotted bridge piers with a semicircular fin[J]. Journal of Hydroelectric Engineering, 2017, 36(4): 26-37. （in Chinese） doi: 10.11660/slfdxb.20170404
[8] 齐洪亮, 袁天刚, 陈贵山, 等. 清水条件下淹没式透水桩群减少圆柱桥墩局部冲刷试验[J]. 长安大学学报(自然科学版),2023,43(2):69-79. (QI Hongliang, YUAN Tiangang, CHEN Guishan, et al. Experimental on local scour around cylindrical pier protected by submerged permeable pile group in clear water[J]. Journal of Chang’an University (Natural Science Edition), 2023, 43(2): 69-79. (in Chinese) QI Hongliang, YUAN Tiangang, CHEN Guishan, et al. Experimental on local scour around cylindrical pier protected by submerged permeable pile group in clear water[J]. Journal of Chang’an University (Natural Science Edition), 2023, 43(2): 69-79. （in Chinese）
[9] 王祚, 牟献友, 李春江, 等. 不同流量下环翼型防冲板结构优化试验[J]. 水利水运工程学报,2015(2):44-49. (WANG Zuo, MOU Xianyou, LI Chunjiang, et al. Experimental studies on structure optimization of ring-wing scour plates under different discharges[J]. Hydro-Science and Engineering, 2015(2): 44-49. (in Chinese) WANG Zuo, MOU Xianyou, LI Chunjiang, et al. Experimental studies on structure optimization of ring-wing scour plates under different discharges[J]. Hydro-Science and Engineering, 2015(2): 44-49. （in Chinese）
[10] DEY S, SUMER B M, FREDSØE J. Control of scour at vertical circular piles under waves and current[J]. Journal of Hydraulic Engineering, 2006, 132(3): 270-279. doi: 10.1061/(ASCE)0733-9429(2006)132:3(270)
[11] WU P, BALACHANDAR R, RAMAMURTHY A. Effects of splitter plate on reducing local scour around bridge pier[J]. River Research and Applications, 2018, 34(10): 1338-1346. doi: 10.1002/rra.3363
[12] 齐梅兰, 周马生, 汤改春. 群桩冲刷及抛石级配与厚度对防护效果的影响[J]. 水利学报,2021,52(6):723-730. (QI Meilan, ZHOU Masheng, TANG Gaichun. Scour at pile groups and effects of riprap gradation and thickness on the scour reduction[J]. Journal of Hydraulic Engineering, 2021, 52(6): 723-730. (in Chinese) QI Meilan, ZHOU Masheng, TANG Gaichun. Scour at pile groups and effects of riprap gradation and thickness on the scour reduction[J]. Journal of Hydraulic Engineering, 2021, 52(6): 723-730. （in Chinese）
[13] 陈振宏. 单向流作用下直立圆柱局部冲刷及其防护的实验研究[D]. 大连: 大连理工大学, 2019. (CHEN Zhenhong. Experimental investigation of local scour and scour protection around vertical piles in steady currents[D]. Dalian: Dalian University of Technology, 2019. (in Chinese) CHEN Zhenhong. Experimental investigation of local scour and scour protection around vertical piles in steady currents[D]. Dalian: Dalian University of Technology, 2019. （in Chinese）
[14] 房世龙, 唐洪武, 周宜林, 等. 桥墩附近四面体透水框架抛投防冲效果试验研究[J]. 水科学进展,2006,17(3):354-358. (FANG Shilong, TANG Hongwu, ZHOU Yilin, et al. Experimental study on effect of local scour at piers and protection by tetrahedron frame[J]. Advances in Water Science, 2006, 17(3): 354-358. (in Chinese) FANG Shilong, TANG Hongwu, ZHOU Yilin, et al. Experimental study on effect of local scour at piers and protection by tetrahedron frame[J]. Advances in Water Science, 2006, 17(3): 354-358. （in Chinese）
[15] 吴迪, 冯卫兵, 石麒琳. 柔性植物消浪及沿程阻流特性试验研究[J]. 人民黄河,2014,36(12):79-81, 84. (WU Di, FENG Weibing, SHI Qilin. A physical model study of the effect of the flexible vegetation on wave height attenuation and along the way of flow structure[J]. Yellow River, 2014, 36(12): 79-81, 84. (in Chinese) doi: 10.3969/j.issn.1000-1379.2014.12.025 WU Di, FENG Weibing, SHI Qilin. A physical model study of the effect of the flexible vegetation on wave height attenuation and along the way of flow structure[J]. Yellow River, 2014, 36(12): 79-81, 84. （in Chinese） doi: 10.3969/j.issn.1000-1379.2014.12.025
[16] 庞翠超. 象限分析法分析沉水植物促淤效应[J]. 水利水运工程学报,2016(3):20-26. (PANG Cuichao. Application of quadrant analysis in analyzing sediment transport in flow with submerged plants[J]. Hydro-Science and Engineering, 2016(3): 20-26. (in Chinese) PANG Cuichao. Application of quadrant analysis in analyzing sediment transport in flow with submerged plants[J]. Hydro-Science and Engineering, 2016(3): 20-26. （in Chinese）
[17] ABT S R, CLARY W P, THORNTON C I. Sediment deposition and entrapment in vegetated streambeds[J]. Journal of Irrigation and Drainage Engineering, 1994, 120(6): 1098-1111. doi: 10.1061/(ASCE)0733-9437(1994)120:6(1098)
[18] 唐洪武, 吕升奇, 龙涧川. 刚性植物条件下静水中粗颗粒泥沙沉速研究[J]. 水利学报,2007,38(10):1214-1220. (TANG Hongwu, LÜ Shengqi, LONG Jianchuan. Settling velocity of coarse sediment particles in still water with rigid vegetation[J]. Journal of Hydraulic Engineering, 2007, 38(10): 1214-1220. (in Chinese) TANG Hongwu, LÜ Shengqi, LONG Jianchuan. Settling velocity of coarse sediment particles in still water with rigid vegetation[J]. Journal of Hydraulic Engineering, 2007, 38(10): 1214-1220. （in Chinese）
[19] XIONG W, TANG P B, KONG B, et al. Computational simulation of live-bed bridge scour considering suspended sediment loads[J]. Journal of Computing in Civil Engineering, 2017, 31(5): 4017040. doi: 10.1061/(ASCE)CP.1943-5487.0000689
[20] 熊文, 姚浩, CAI C S, 等. 考虑悬移质效应的桥墩动床冲刷精细化分析方法[J]. 湖南大学学报(自然科学版),2016,43(5):52-60. (XIONG Wen, YAO Hao, CAI C S, et al. Bridge scour simulation in live-bed condition with suspended load[J]. Journal of Hunan University (Natural Sciences), 2016, 43(5): 52-60. (in Chinese) XIONG Wen, YAO Hao, CAI C S, et al. Bridge scour simulation in live-bed condition with suspended load[J]. Journal of Hunan University (Natural Sciences), 2016, 43(5): 52-60. （in Chinese）
[21] 龙庆. 挟沙水流下桥墩局部冲刷数值模拟研究[D]. 合肥: 合肥工业大学, 2020. (LONG Qing. Numerical simulation study on local scour of bridge pier under sand-laden flow[D]. Hefei: Hefei University of Technology, 2020. (in Chinese) LONG Qing. Numerical simulation study on local scour of bridge pier under sand-laden flow[D]. Hefei: Hefei University of Technology, 2020. （in Chinese）
[22] 陈明, 娄厦, 刘曙光, 等. 刚性沉水植物影响下波浪传播及泥沙悬浮数值模拟[J]. 同济大学学报(自然科学版),2022,50(6):861-870. (CHEN Ming, LOU Sha, LIU Shuguang, et al. Numerical simulation of wave propagation and sediment suspension affected by submerged rigid vegetation[J]. Journal of Tongji University (Natural Science), 2022, 50(6): 861-870. (in Chinese) doi: 10.11908/j.issn.0253-374x.21368 CHEN Ming, LOU Sha, LIU Shuguang, et al. Numerical simulation of wave propagation and sediment suspension affected by submerged rigid vegetation[J]. Journal of Tongji University (Natural Science), 2022, 50(6): 861-870. （in Chinese） doi: 10.11908/j.issn.0253-374x.21368
[23] 陈铭, 彭国平, 王浩, 等. 桥墩局部冲刷三维地形及水流结构特性试验研究[J]. 水力发电学报,2021,40(11):13-24. (CHEN Ming, PENG Guoping, WANG Hao, et al. Experimental study on three-dimensional topography and flow structure around bridge piers under local scour[J]. Journal of Hydroelectric Engineering, 2021, 40(11): 13-24. (in Chinese) doi: 10.11660/slfdxb.20211102 CHEN Ming, PENG Guoping, WANG Hao, et al. Experimental study on three-dimensional topography and flow structure around bridge piers under local scour[J]. Journal of Hydroelectric Engineering, 2021, 40(11): 13-24. （in Chinese） doi: 10.11660/slfdxb.20211102
[24] 侯志军, 侯佼建, 伊晓燕. 并线桥墩局部冲刷试验研究[J]. 泥沙研究,2021,46(1):74-80. (HOU Zhijun, HOU Jiaojian, YI Xiaoyan. Experimental study on local erosion of bridge group piers[J]. Journal of Sediment Research, 2021, 46(1): 74-80. (in Chinese) HOU Zhijun, HOU Jiaojian, YI Xiaoyan. Experimental study on local erosion of bridge group piers[J]. Journal of Sediment Research, 2021, 46(1): 74-80. （in Chinese）
[25] 杨元平, 张芝永, 李最森, 等. 跨海桥梁基础冲刷特征研究[J]. 水利水运工程学报,2021(4):131-137. (YANG Yuanping, ZHANG Zhiyong, LI Zuisen, et al. Scour features of sea-crossing bridge piers[J]. Hydro-Science and Engineering, 2021(4): 131-137. (in Chinese) doi: 10.12170/20210105002 YANG Yuanping, ZHANG Zhiyong, LI Zuisen, et al. Scour features of sea-crossing bridge piers[J]. Hydro-Science and Engineering, 2021(4): 131-137. （in Chinese） doi: 10.12170/20210105002
[26] SAGHRAVANI S F, AZHARI A. Simulation of clear water local scour around a group of bridge piers using an Eulerian 3D, two-phase model[J]. Progress in Computational Fluid Dynamics: an International Journal, 2012, 12(5): 333-341. doi: 10.1504/PCFD.2012.049097
[27] VOSKOBOINICK A, VOSKOBOINICK V, TURICK V, et al. Interaction of group of bridge piers on scour[C]∥HU Z, PETOUKHOV S, DYCHKA I, et al. International Conference on Computer Science, Engineering and Education Applications. Cham: Springer, 2021: 3-17.
[28] 李德娟. 沙质河床多排圆柱桥墩间距对局部冲刷影响试验研究[D]. 合肥: 合肥工业大学, 2022. (LI Dejuan. Experimental study on influence of multi-row cylindrical pier spacing on local scour in sandy river bed[D]. Hefei: Hefei University of Technology, 2022. (in Chinese) LI Dejuan. Experimental study on influence of multi-row cylindrical pier spacing on local scour in sandy river bed[D]. Hefei: Hefei University of Technology, 2022. （in Chinese）
[29] DEBNATH K, CHAUDHURI S. Effect of suspended sediment concentration on local scour around cylinder for clay-sand mixed sediment beds[J]. Engineering Geology, 2011, 117(3): 236-245.
[30] OBIED N A, KHASSAF S I. Experimental study for protection of piers against local scour using slots[J]. International Journal of Engineering, 2019, 32(2): 217-222.
[31] MASTBERGEN D R, VAN DEN BERG J H. Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons[J]. Sedimentology, 2003, 50(4): 625-637. doi: 10.1046/j.1365-3091.2003.00554.x
[32] SOUISBY R. Bedload transport[C]∥Dynamics of Marine Sands. Wellington: The Institution of Civil Engineers (ICE) Publishing, 1997: 155-170.
[33] MEYER-PETER E, MULLER R. Formulas for bed-load transport[C]∥Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research. Delft: International Association Hydraulic Research, 1948: 39-64.
[34] VAN RIJN L C. Sediment transport, part I: bed load transport[J]. Journal of Hydraulic Engineering, 1984, 110(10): 1431-1456. doi: 10.1061/(ASCE)0733-9429(1984)110:10(1431)
计量
- 文章访问数: 203
- HTML全文浏览量: 33
- PDF下载量: 203
