Email Alerts
RSS
Ultimate bearing capacity and safety assessment of roller-compacted concrete gravity dams
-
摘要:
大坝安全一直是水利工程重点关注的问题，对坝体极限承载能力的探究和安全评估可更好指导工程设计及维护。结合某碾压混凝土重力坝工程，采用水头超载法、容重超载法和强度折减法进行有限元仿真计算，并进行极限承载能力评估，确定其安全系数。结果表明，水头超载法对碾压混凝土重力坝极限承载能力的影响更加敏感，但在实际工程中应采用强度折减法来确定坝体的安全系数，其取值更加准确。该研究系统阐述了3种评估极限承载能力方法下坝体模型的破坏机理，明确了强度折减法在实际工程中确定重力坝极限承载能力的准确性，可为其他工程极限承载能力评估仿真计算提供借鉴。
Abstract:Dam safety has always been a critical concern in hydraulic engineering. Investigating the ultimate bearing capacity of dam structures and conducting safety assessments provide valuable guidance for engineering design and maintenance. This study examines a roller-compacted concrete gravity dam, employing the head overload method, unit weight overload method, and strength reduction method for finite element simulations. The ultimate bearing capacity is evaluated, and the safety factor is determined. The results reveal that the head overload method is more sensitive in assessing the ultimate bearing capacity of roller-compacted concrete gravity dams. However, the strength reduction method should be prioritized in practical engineering applications for determining the safety factor, as it yields more accurate values. This study systematically elucidates the failure mechanisms of the dam model under the three evaluation methods and highlights the accuracy of the strength reduction method in determining the ultimate bearing capacity of gravity dams in real-world scenarios. These findings provide a reference for simulation-based evaluations of ultimate bearing capacity in other engineering projects.
-
大坝安全一直是水利建设的重中之重，大坝的设计、施工、运行和维护，无一不要求对大坝安全做出严苛的规范。20世纪80年代以来，碾压混凝土重力坝作为一种新型筑坝技术，以其浇筑速度快、施工简单、造价低等优点得到大规模的设计应用，相较于常态混凝土重力坝，具有单位体积胶凝材料用量和单位体积用水量少的特点。随着碾压混凝土坝技术的快速发展，其施工运行的安全性也受到了越来越多的关注。许多学者开展了碾压混凝土坝极限承载能力的研究，并对工程进行安全评估，以保障大坝的运行安全，如朱伯芳[1]院士讨论了混凝土坝安全评估的必要性，并通过强度递减法和超载法的对比分析，明确了工程应采用有限元全程仿真与强度递减法进行安全评估；熊堃等[2]分别采用容重超载法、强度折减法和综合法计算了桑郎拱坝的整体超载系数；赵磊等[3]结合古贤碾压混凝土重力坝，系统阐述了容重超载法和水头超载法对坝体极限承载能力分析的差异；舒建国等[4]利用有限元超载法对重力坝的深层抗滑稳定进行分析，从而确定重力坝的抗滑稳定安全系数；于沭等[5]结合向家坝工程研究将强度折减法用于重力坝深层抗滑稳定性工程分析；李征等[6]采用超载法和综合法对复杂地基上的重力坝进行整体稳定及破坏过程研究，认为两者模拟的大坝破坏失稳过程结果可相互印证，为综合法的应用提供参考；王河等[7]基于有限元超载-折减综合法探究了混凝土重力坝的深层抗滑稳定性分析，结果表明超载-折减综合法计算的安全系数较单独的超载、强度折减法更加安全合理；周伟等[8]结合向家坝研究了高混凝土重力坝复杂坝基稳定安全度及极限承载能力，认为系统的极限承载能力由夹泥层强度控制。
上述研究成果为大坝极限承载能力检测和工程安全评估提供了极大帮助，但这些研究重点关注于重力坝的失稳破坏研究，即将重力坝坝体作为整体分析重力坝的抗滑稳定性，忽略了重力坝作为复杂的坝体结构，其本身的材料特性即局部区域的材料屈服，也没有详细分析3种评估方法对坝体破坏机理表述的差异。本文结合某碾压混凝土重力坝工程，建立能反映坝基地质状况、大坝主要结构的有限元计算模型，采用反演后的材料参数，进行非线性有限元分析，探究不同极限承载力下重力坝的破坏机理，分析讨论大坝的变形状况，并做出安全评估，以寻求更符合实际工程的仿真计算方法。
1. 工程概况
某抽水蓄能电站枢纽工程主要包括上水库、输水系统、发电厂房、下水库等主要建筑物，其下水库挡水坝为碾压混凝土重力坝，下水库总库容为
1248 万m3，坝高108.0 m，坝顶全长225.0 m，所在建基面高程198.0 m，坝顶高程306.0 m，泄洪建筑物包括溢流表孔和泄洪底孔。该抽水蓄能电站地处亚热带海洋性气候，坝区多年平均气温19.3 ℃，坝区月平均气温见表1。表 1 坝区月平均气温Table 1. Monthly average temperature in the dam area月份 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 气温/ ℃ 9.2 10.3 13.6 18.8 22.9 25.3 27.5 27.3 25.0 21.7 18.2 12.0 2. 计算模型及材料参数
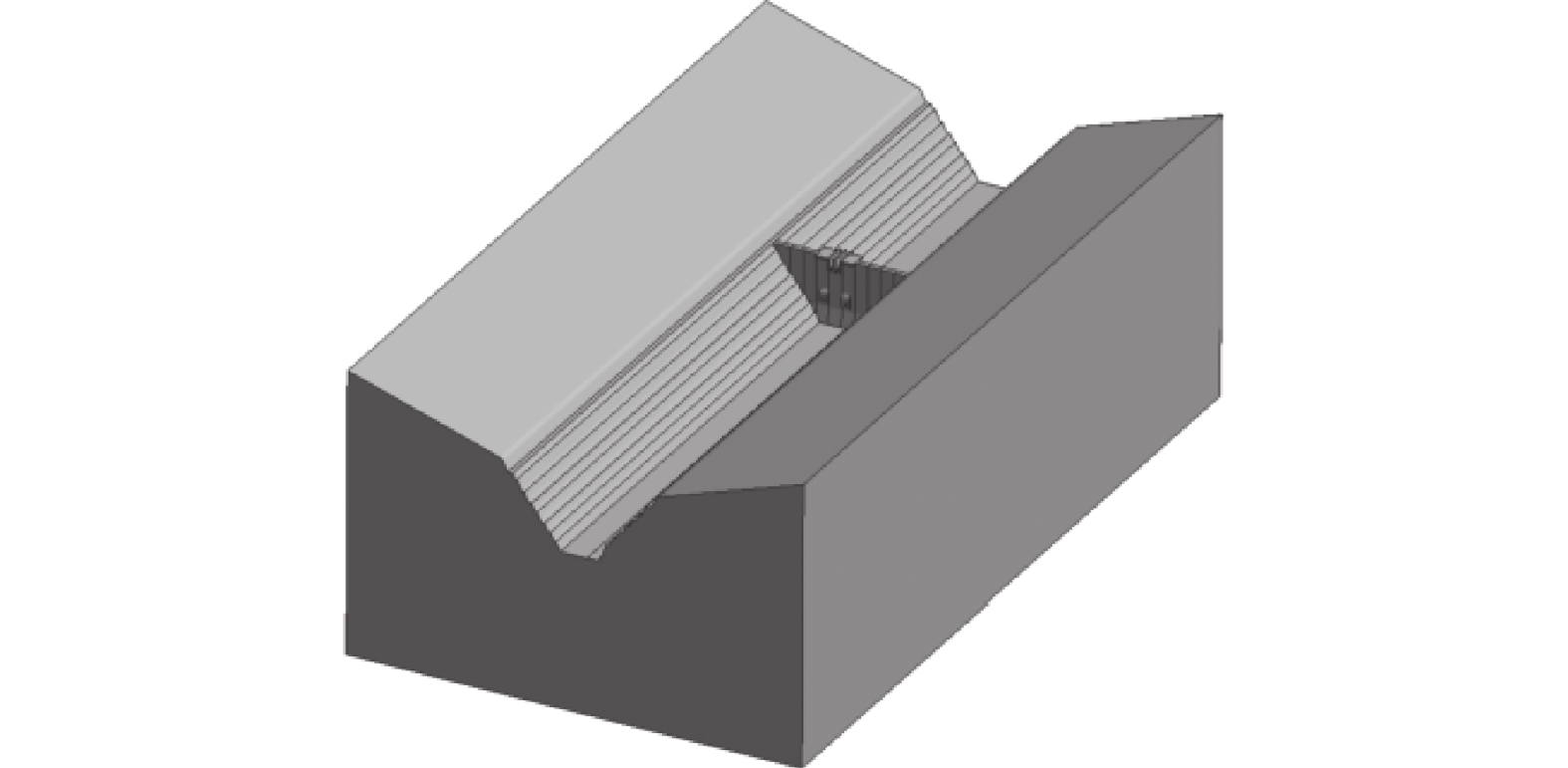
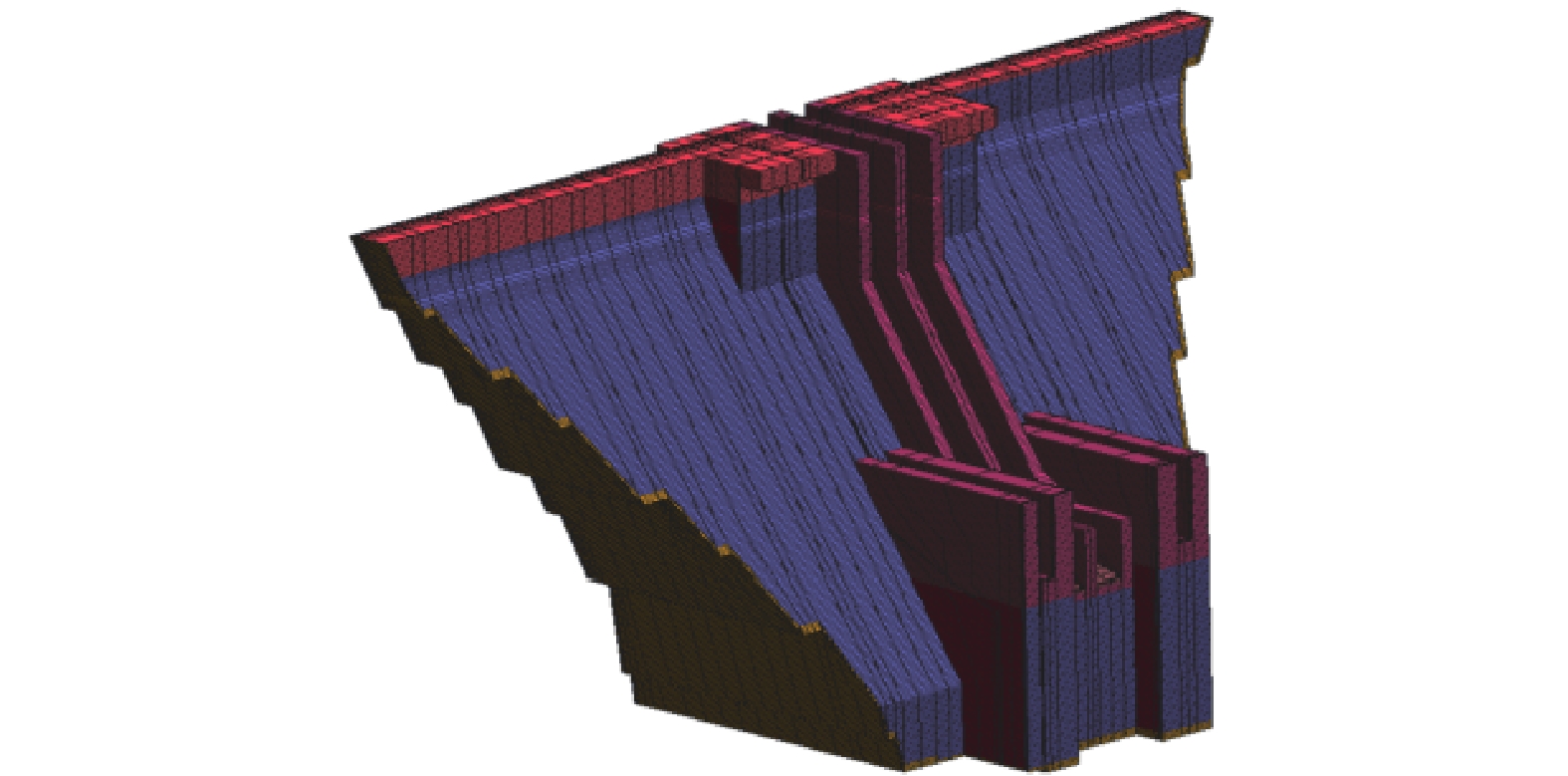
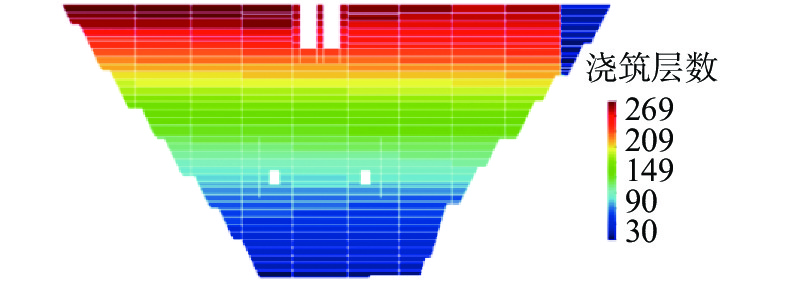
坝体及地基计算模型见图1。对坝体及地基进行网格划分，其中坝体单元数141 937，地基单元数157 886，总单元数299 823，总节点数330 576，模型网格划分见图2。坝体模型以实际工程施工进度进行模型浇筑，浇筑方式为跳仓浇筑，每仓均设置冷却水管，见图3，模型地基部分采用底面全约束和四周法向约束，约束边界图见图4。采用非线性超载进行计算分析，考虑上游水压及坝体自重荷载，上游水位为正常蓄水位299.0 m，下游无水，模型荷载面示意图见图5，模型未考虑渗流和地质断层。坝体材料参数见表2，各材料参数为仿真反演后的参数结果。
表 2 坝体材料的计算参数Table 2. Calculation parameters of dam materials部位 坝体混凝土材料 密度/（kg/m3） 弹性模量/GPa 泊松比 抗拉强度/MPa 抗压强度/MPa Mohr-Coulomb 屈服准则 内摩擦角/( °) 黏聚力/MPa 下游坝面 C15变态三级配 2 390 27.5 0.19 1.92 20.7 45 1.99 坝体内部 C15碾压三级配 2 400 32.8 0.17 2.03 18.4 45 1.89 坝顶及基础垫层 C20常态三级配 2 400 30.0 0.17 2.0 20.0 45 2.00 闸墩、表孔导墙、溢流面 C25常态二级配 2 410 37.4 0.19 2.15 41.8 45 2.00 上游坝面 C25变态二级配 2 390 27.5 0.19 2.53 28.5 45 2.52 上游防渗 C25碾压二级配 2 360 32.2 0.17 2.39 27.8 45 2.24 溢流面抗冲耐磨 C40常态二级配 2 410 37.4 0.19 2.22 23.0 45 2.05 3. 基本原理及方法
3.1 极限承载的评价方法及安全评估
为了对碾压混凝土坝的极限承载能力和安全进行较准确的评估，本文采用3种方法进行计算分析，分别为超载法（水头超载法、容重超载法）和强度折减法。
（1）超载法包括水头超载法和容重超载法。在保证坝体和地基材料特性不变的情况下，增加上、下游水荷载的超载系数，研究坝体和地基破坏过程与超载系数的关系。水头超载法采用逐步增加水位实现超载过程，容重超载法通过逐步增加水容重达到超载效果。
水头超载系数计算公式为：
$$ {K}_{\rm P}=P^{'}/P $$ (1) 式中：KP为水头超载系数；$P^{'} $为超载系数对应的上游水荷载；P为正常蓄水位对应的上游水荷载。
本文以正常蓄水位为起始水头，先以10 m，后以5 m水头为计算步长逐渐累加，直到坝体出现贯通性屈服区时，此时的超载系数即为水头超载安全系数。
容重超载系数计算公式为：
$$ {K}_{\rm g}={\gamma }^{'}/\gamma $$ (2) 式中：Kg为重度超载系数；${\gamma }^{'} $为超载系数对应的水重度；γ为水重度。
本文以正常水荷载（Kg=1.0）为初始超载系数，以步长0.2递增进行计算，直到坝体出现贯通性屈服区时，此时的超载系数为容重超载安全系数。
（2）强度折减法，保持坝体和地基所受荷载不变，降低坝体和地基材料的黏聚力和内摩擦角，研究坝体及地基的极限承载能力及其安全系数[7]。安全系数计算式为：
$$ {K}_{\rm f}=c^{'}/c $$ (3) $$ {\varphi }{^{'}}={\rm arctan}\dfrac{{\rm tan}\varphi }{{K}_{\rm f}} $$ (4) 式中：Kf为强度折减系数；c、φ分别为坝体及地基的黏聚力和内摩擦角；${c }{^{'}} $、${\varphi }{^{'}} $分别为折减后的黏聚力和内摩擦角。
本文初始材料强度系数为1，以步长0.05递减进行计算，当坝体出现贯通性屈服区时，此时的强度折减系数即为强度折减的安全系数。
对于复杂工程，通常在整体结构破坏前，次要结构的破坏早已发生。结构破坏过程一般分为3个阶段，即弹性变形阶段、塑性变形阶段和全面破坏阶段[9-10]。目前常用的评判坝体及地基破坏或失去承载能力的方法有以下几种：有限元解收敛性判据，在迭代求解过程中，计算常常因为结构的位移增量或者荷载增量达到极值后，出现迭代过程不收敛的情况，以此作为结构失稳的判据[11-12]； 屈服区贯通，在不断地加载或降低材料强度的条件下，坝体及地基会逐渐产生屈服，屈服区逐渐扩散直至贯通整个坝体，大坝失去承载能力，结构整体失稳[13]；特征量突变，随着荷载的增大或材料强度的降低，若结构处于安全状态，特征量的变化应该是线性的，当某一特征量出现明显突变时，可认为结构已发生破坏，其所对应的超载系数或强度折减系数作为安全评估的判据[14]。
3.2 本构模型及屈服准则
坝体及地基的本构模型采用非线性的弹塑性模型，该工程的屈服准则为混凝土采用Mohr-Coulomb（简称“M-C”）屈服准则，基岩采用Drucker-Prager（简称“D-P”）屈服准则，Drucker-Prager屈服条件为：
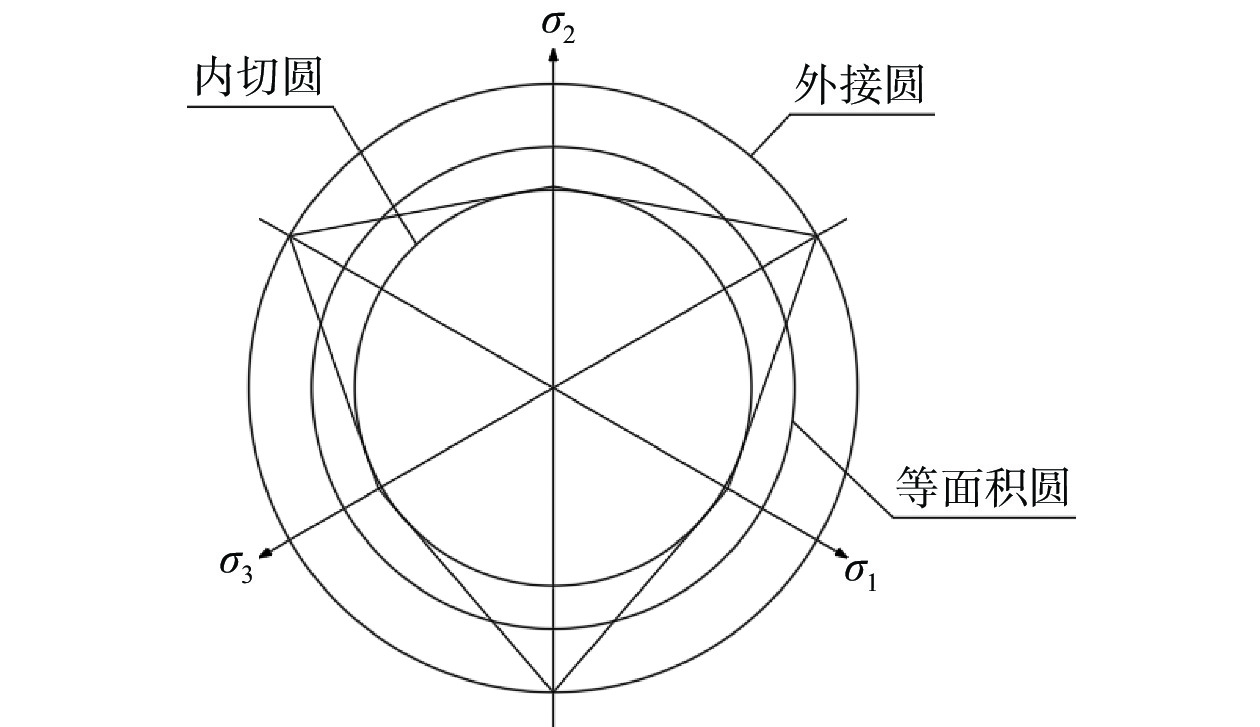
$$ f=\alpha {I}_{1}+\sqrt{{J}_{2}}-k=0 $$ (5) 式中：I1为应力张量的第一不变量；J2为应力偏张量的第二不变量；$ \alpha $、k为与材料摩擦角$\varphi $和黏聚力c有关的常数。在确定参数a和k时，可与Mohr-Coulomb屈服条件相比较。在π平面上，M-C屈服条件是一六边形，D-P屈服条件是一圆形，如图6所示，不同的D-P圆对应不同的$ \alpha $、k参数。
![]()
图 6 摩尔-库伦准则和Drucker-Prager准则Figure 6. Mohr-Coulomb criterion and Drucker-Prager criterion外接圆时：
$$ \left\{\begin{array}{c}\alpha =\dfrac{2\mathrm{sin}\varphi }{\sqrt{3}\left(3-\mathrm{sin}\varphi \right)}\\ k=\dfrac{6c\;\mathrm{cos}\varphi }{\sqrt{3}\left(3-\mathrm{sin}\varphi \right)}\end{array}\right. $$ (6) 内切圆时：
$$ \left\{\begin{array}{c}\alpha =\dfrac{2\mathrm{sin}\varphi }{\sqrt{3}\left(3+\mathrm{sin}\varphi \right)}\\ k=\dfrac{6c\;\mathrm{cos}\varphi }{\sqrt{3}\left(3+\mathrm{sin}\varphi \right)}\end{array}\right. $$ (7) 等面积圆时：
$$ \left\{\begin{array}{c}\alpha =\dfrac{2\sqrt{3}\mathrm{sin}\varphi }{\sqrt{2\sqrt{3}\pi \left(9-{\mathrm{sin}}^{2}\varphi \right)}} \\ k=\dfrac{6\sqrt{3}c\;\mathrm{cos}\varphi }{\sqrt{2\sqrt{3}\pi \left(9-{\mathrm{sin}}^{2}\varphi \right)}}\end{array}\right. $$ (8) 为探究碾压混凝土坝的极限承载能力，本文采用外接圆方式确定Drucker-Prager屈服准则相应参数。
4. 极限承载能力分析及安全评估
本文从坝体顺河向位移、屈服情况和破坏模式三方面分析承载能力，对比3种计算结果的差异，并进行安全评估，为实际工程提供借鉴。
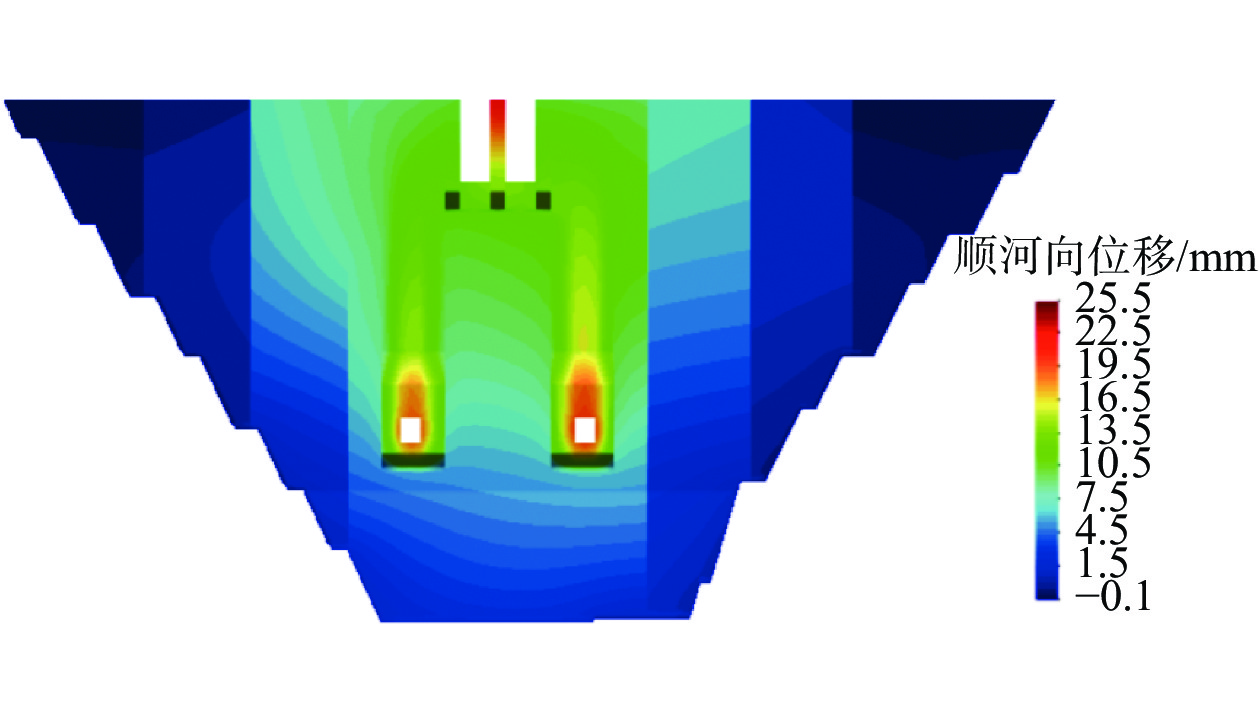
4.1 顺河向位移分析
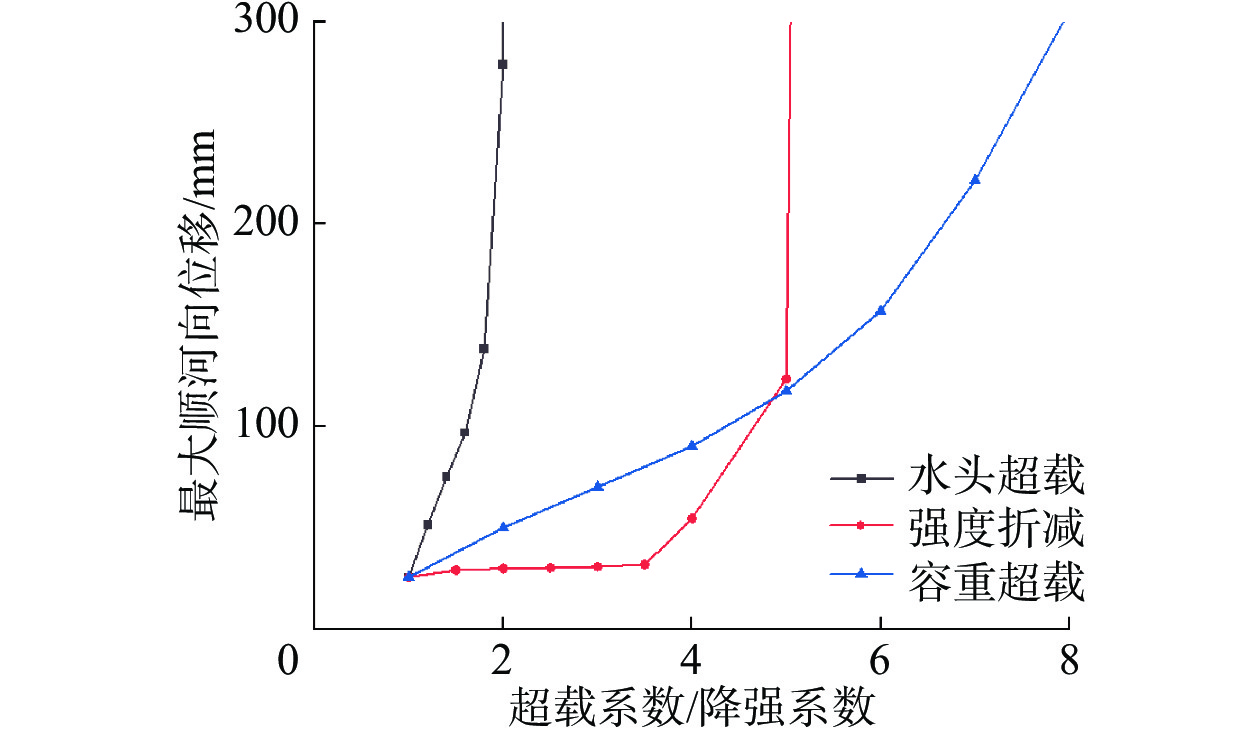
正常蓄水位时坝体上游面顺河向位移云图见图7，3种方式下坝体最大顺河向位移见图8。依据特征量突变评判方法，可见在水头超载方式下，超载系数为1.0~1.6时坝体最大顺河向位移基本呈直线，超过2.0后坝体最大顺河向位移发生突变，结构失稳；强度折减方式下，强度折减系数小于3.5时坝体最大顺河向位移基本呈直线发展，大于3.5后坝体最大顺河向位移发生突变，结构失稳；容重超载方式下，超载系数小于5.0时坝体最大顺河向位移基本呈直线，超载系数大于5.0后坝体最大顺河向位移发生突变，结构失稳。对比3种方式下坝体最大顺河向位移结果，坝体受水头超载影响更加敏感。
![]()
图 7 正常蓄水位（安全系数为1）时的坝体上游面顺河向位移Figure 7. Upstream displacement along the river direction of the dam body at normal reservoir water level (safety factor = 1)![]()
图 8 3种方式下坝体最大顺河向位移过程线Figure 8. Maximum river-oriented displacement of the dam body under three methods4.2 屈服情况及破坏模式分析
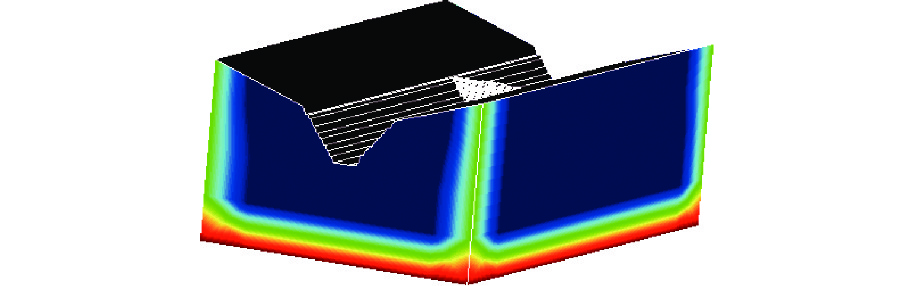
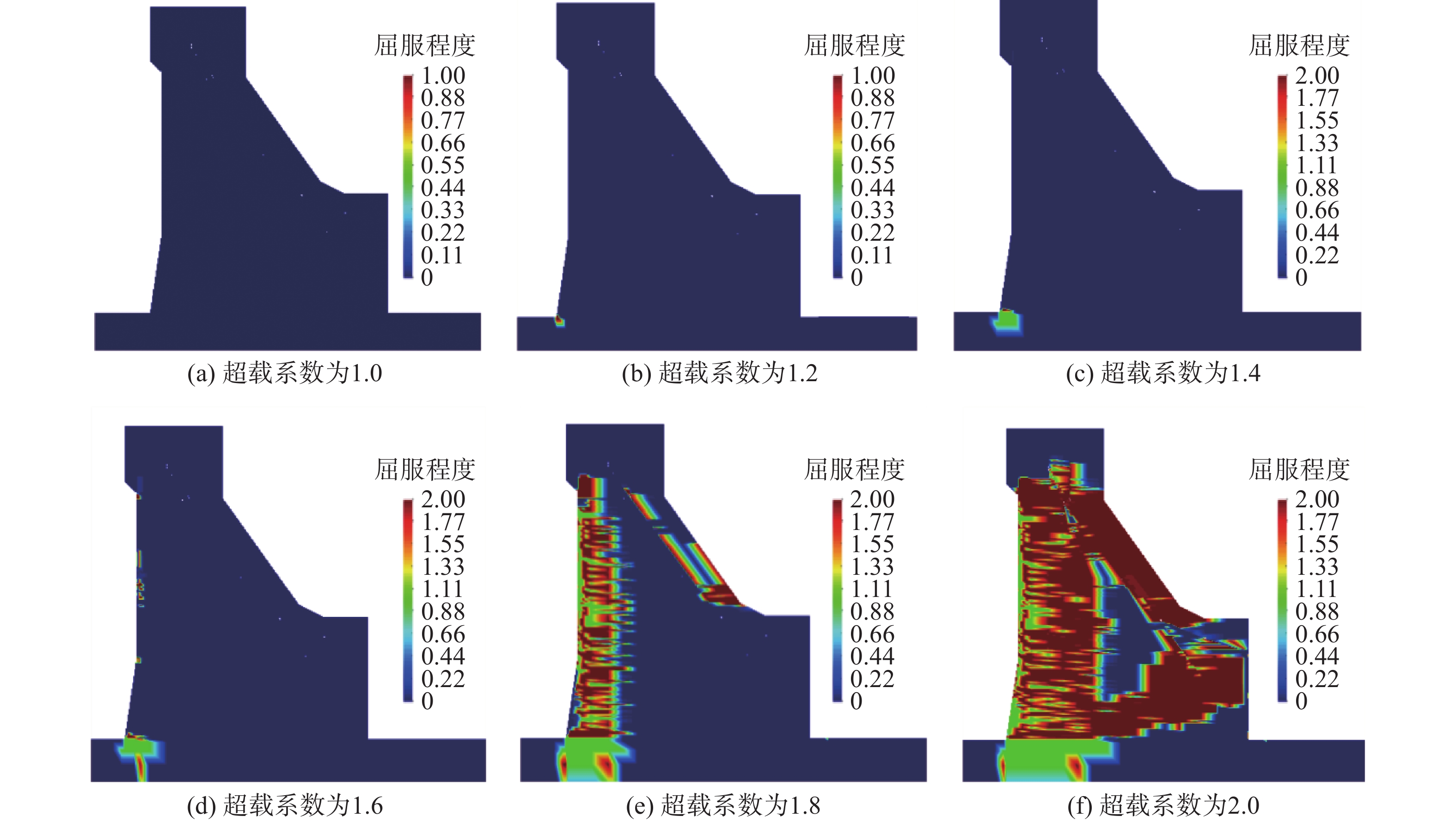
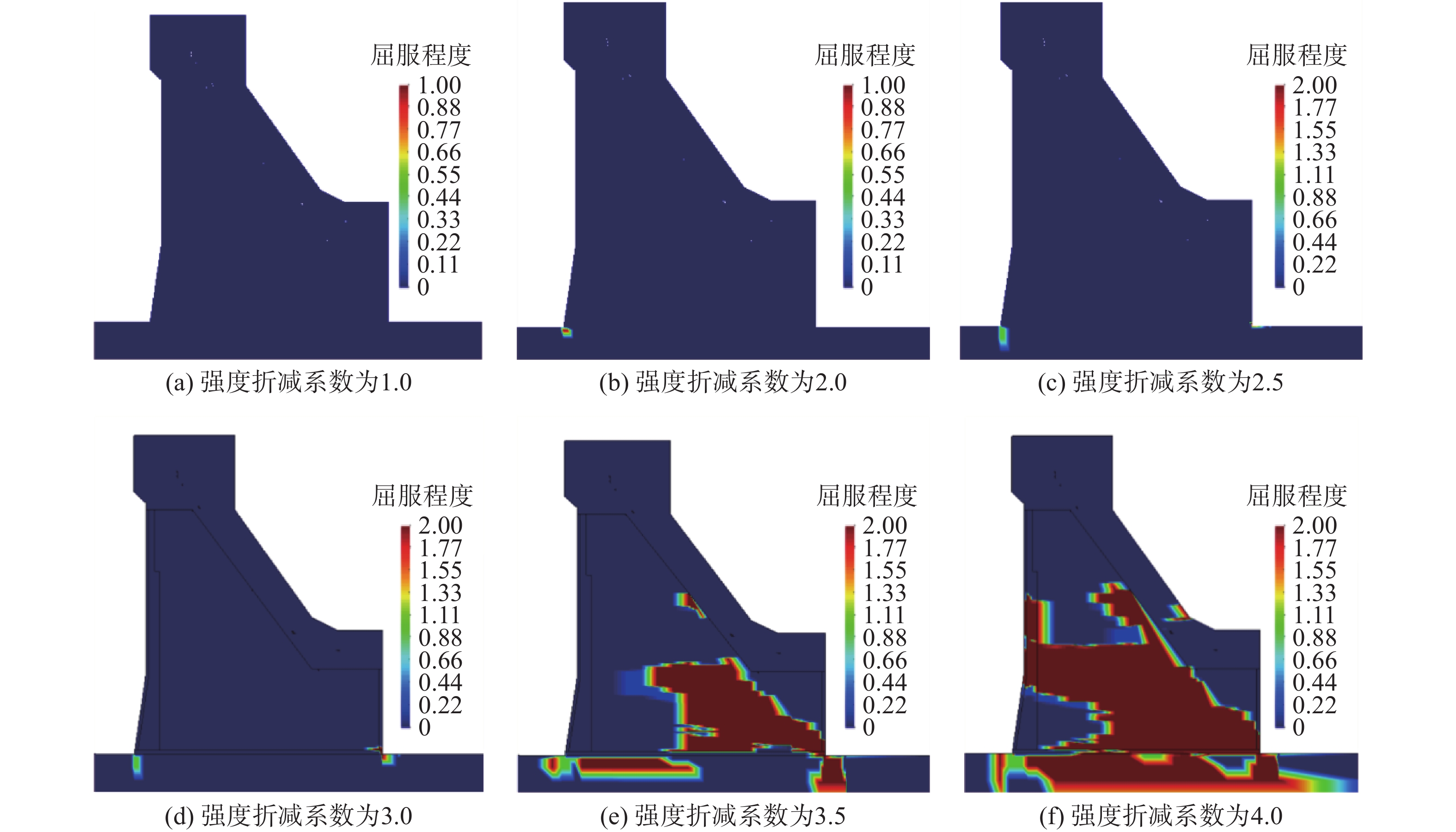
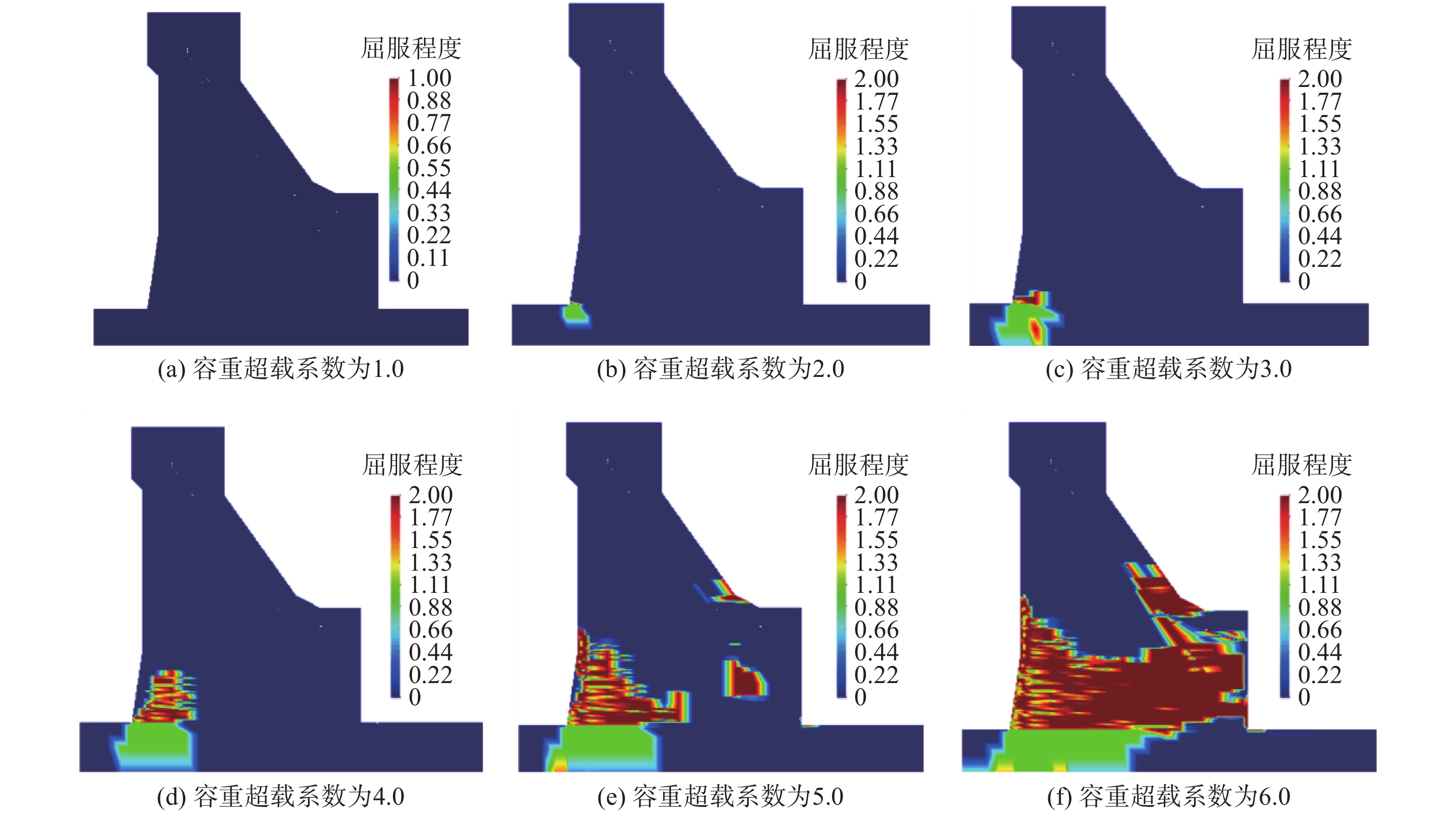
3种方式下坝体典型截面屈服图如图9、图10和图11所示，依据屈服区贯通评判方法，可见在水头超载方式下，超载系数为1.4时开始产生小范围屈服，1.6时屈服区扩大，大于2.0后屈服区贯通，结构失稳；降强方式下，折减系数为2.0时产生屈服，3.0时坝址处产生屈服，3.5时屈服范围逐渐扩大，4.0时坝体屈服区贯通，结构整体失稳；容重超载方式下，超载系数为3.0时坝踵处小范围屈服，5.0时屈服范围扩大，6.0时坝体屈服区贯通，结构整体失稳。
![]()
图 9 不同水头超载系数下坝体典型剖面屈服Figure 9. Yield of typical dam cross-sections under different water head overload coefficients![]()
图 10 不同强度折减系数下坝体典型截面屈服Figure 10. Yield of typical dam cross-sections under different strength reduction coefficients![]()
图 11 不同容重超载系数下坝体典型截面屈服Figure 11. Yield of typical dam cross-sections under different unit weight overload coefficients共性分析，3种方式下最先产生屈服的区域均为坝体及地基结构薄弱区域，在实际工程上应予以重视。由屈服图可知，最先产生屈服的区域为坝踵处地基，说明在超载和强度折减情况下，该部位地基和混凝土易受因拉应力过大产生破坏，这要求坝体选址和施工方面应更加严格，坝踵处尽量避免出现断层、软弱夹层等危险结构，工程上应采取加固或提高材料强度等措施，保证大坝安全性。
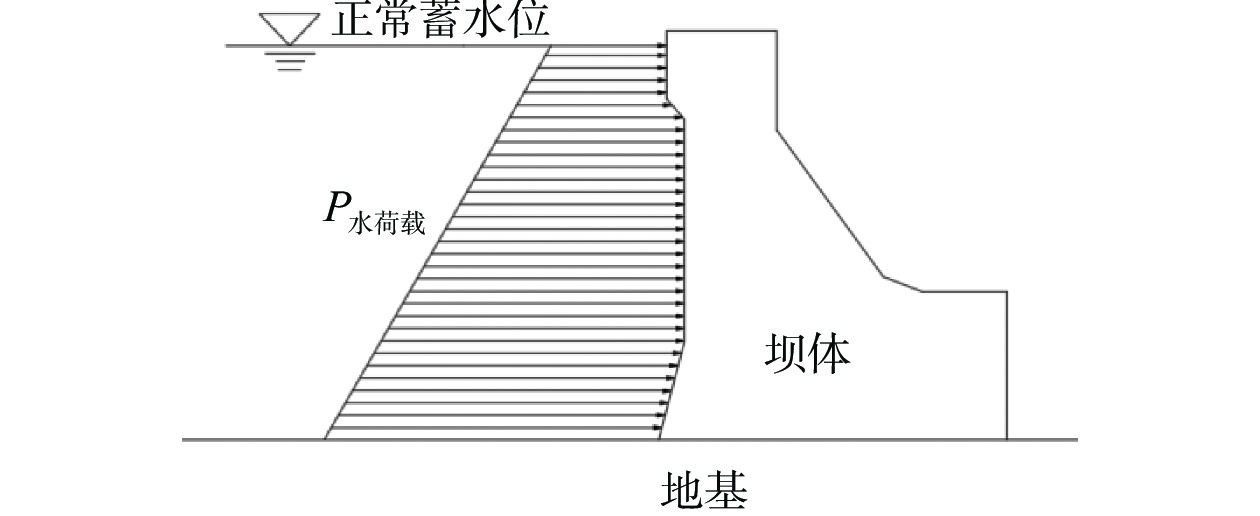
差异性分析，3种方式下大坝虽然都是从坝踵处开始产生屈服，但最后的屈服情况和破坏模式并不完全相同。水头超载的加载方式是通过提高上游水位，其水荷载加载方式为梯形加载（图12），首先产生屈服的是通过悬臂梁作用的坝踵处，随着水荷载的不断增加，导致结构整体的拉应力增大，受拉屈服扩大逐渐延伸至整个上游坝面，再通过坝体应力调整向下游坝面扩大，直至贯通；容重超载仿真计算时水荷载分布方式呈三角形（图13），坝体上部的荷载力较小，上游坝面的屈服集中在其下部，通过应力调整向下游扩大，直至屈服。由于两种超载法都增大了荷载力，导致整体结构拉应力增大，屈服面均呈现出了从上游向下游扩大的趋势。而强度折减法的水荷载分布也呈三角形分布，但强度折减法降低了坝体及地基的强度，导致上游水荷载推力大于坝体与地基间的凝聚力以及坝基面产生的摩擦力，坝体与地基间产生滑动破坏，坝体从下游处开始屈服，且伴有地基的明显屈服，总体上屈服是由下游向上游传递。
4.3 对比评价
对比3种方式下坝体最大顺河向位移和屈服情况，可以看出坝体受水头超载影响更加敏感，其安全系数为坝体未失稳时的最大超载系数为1.6；容重超载的安全度最高，安全系数为屈服区贯通时的最大超载系数为5.0；而降强安全系数介于两者之间，为3.5。
工程经验表明，重力坝失稳破坏的主要形式为滑动破坏，当发生坝体屈服破坏时滑动破坏已经发生，导致坝体不可能有很大的超载能力，故本文计算得到的安全系数比实际重力坝的抗滑稳定安全系数大。对于地基岩石完整性较好的坝体，考虑坝体与地基黏聚力时重力坝的抗滑稳定安全系数要求不得小于3.0[15]，超载法得出的安全系数就不太合理，因为在工程运行过程中水荷载增大的倍数有限，一般不会超出正常设计值太多，并且水荷载的增大会导致坝体拉应力范围增大，这就导致了仿真计算失真[1]。强度折减法得出的安全系数相对合理，且重力坝坝体大多是由始于坝趾并顺着坝基面向上游发展的剪切屈服区造成的[16]，这与强度折减法下的破坏过程相似，故在重力坝的极限承载力计算中可采用强度折减法进行安全系数的确定。
5. 结 语
本文通过仿真模型计算分析，总结了水头超载法、容重超载法和强度折减法的破坏机理，在此基础上，对比了3种方法评估大坝极限承载力的优劣，主要结论如下：
（1）通过位移分析和屈服破坏情况分析重力坝的极限承载能力和安全系数，重力坝的顺河向位移和屈服破坏在水头超载法下更加敏感，安全系数也更低，容重超载法下安全系数最高，强度折减法介于两者之间。
（2）实际工程中重力坝的失稳通常为滑动破坏，在忽略坝体节理、断层等情况下，强度折减法仿真计算得到的安全系数满足规范要求的重力坝抗滑稳定安全系数。
（3）超载法和强度折减法可用来确定坝体及地基结构薄弱区域，由于超载法和强度折减法作用机理的不同，对于重力坝极限承载能力采取强度折减法进行安全评估更加准确。
-
![]()
图 6 摩尔-库伦准则和Drucker-Prager准则
Figure 6. Mohr-Coulomb criterion and Drucker-Prager criterion
![]()
图 7 正常蓄水位（安全系数为1）时的坝体上游面顺河向位移
Figure 7. Upstream displacement along the river direction of the dam body at normal reservoir water level (safety factor = 1)
![]()
图 8 3种方式下坝体最大顺河向位移过程线
Figure 8. Maximum river-oriented displacement of the dam body under three methods
![]()
图 9 不同水头超载系数下坝体典型剖面屈服
Figure 9. Yield of typical dam cross-sections under different water head overload coefficients
![]()
图 10 不同强度折减系数下坝体典型截面屈服
Figure 10. Yield of typical dam cross-sections under different strength reduction coefficients
![]()
图 11 不同容重超载系数下坝体典型截面屈服
Figure 11. Yield of typical dam cross-sections under different unit weight overload coefficients
表 1 坝区月平均气温
Table 1 Monthly average temperature in the dam area
月份 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 气温/ ℃ 9.2 10.3 13.6 18.8 22.9 25.3 27.5 27.3 25.0 21.7 18.2 12.0 
下载: 导出CSV
表 2 坝体材料的计算参数
Table 2 Calculation parameters of dam materials
部位 坝体混凝土材料 密度/（kg/m3） 弹性模量/GPa 泊松比 抗拉强度/MPa 抗压强度/MPa Mohr-Coulomb 屈服准则 内摩擦角/( °) 黏聚力/MPa 下游坝面 C15变态三级配 2 390 27.5 0.19 1.92 20.7 45 1.99 坝体内部 C15碾压三级配 2 400 32.8 0.17 2.03 18.4 45 1.89 坝顶及基础垫层 C20常态三级配 2 400 30.0 0.17 2.0 20.0 45 2.00 闸墩、表孔导墙、溢流面 C25常态二级配 2 410 37.4 0.19 2.15 41.8 45 2.00 上游坝面 C25变态二级配 2 390 27.5 0.19 2.53 28.5 45 2.52 上游防渗 C25碾压二级配 2 360 32.2 0.17 2.39 27.8 45 2.24 溢流面抗冲耐磨 C40常态二级配 2 410 37.4 0.19 2.22 23.0 45 2.05
下载: 导出CSV
-
[1] 朱伯芳. 混凝土坝安全评估的有限元全程仿真与强度递减法[J]. 水利水电技术,2007,38(1):1-6. (ZHU Bofang. Finite element whole course simulation and sequential strength reduction method for safety appraisal of concrete dams[J]. Water Resources and Hydropower Engineering, 2007, 38(1): 1-6. (in Chinese) ZHU Bofang. Finite element whole course simulation and sequential strength reduction method for safety appraisal of concrete dams[J]. Water Resources and Hydropower Engineering, 2007, 38(1): 1-6. （in Chinese）
[2] 熊堃, 何蕴龙, 肖伟. 桑郎拱坝整体稳定安全度数值分析[J]. 武汉大学学报(工学版),2007,40(4):22-30. (XIONG Kun, HE Yunlong, et al. Numerical analysis of stability of Sanglang arch dam[J]. Engineering Journal of Wuhan University, 2007, 40(4): 22-30. (in Chinese) XIONG Kun, HE Yunlong, et al. Numerical analysis of stability of Sanglang arch dam[J]. Engineering Journal of Wuhan University, 2007, 40(4): 22-30. （in Chinese）
[3] 赵磊, 贾金生, Mohamed Ramadan, 等. 古贤碾压混凝土重力坝的坝体极限承载能力研究[J]. 水力发电,2023,49(5):51-57, 70. (ZHAO Lei, JIA Jinsheng, RAMADAN M, et al. Study on the ultimate bearing capacity of Guxian RCC gravity dam[J]. Water Power, 2023, 49(5): 51-57, 70. (in Chinese) doi: 10.3969/j.issn.0559-9342.2023.05.010 ZHAO Lei, JIA Jinsheng, RAMADAN M, et al. Study on the ultimate bearing capacity of Guxian RCC gravity dam[J]. Water Power, 2023, 49(5): 51-57, 70. （in Chinese） doi: 10.3969/j.issn.0559-9342.2023.05.010
[4] 舒建国, 程昌勇. 基于有限元超载法的重力坝深层抗滑稳定分析[J]. 广东水利水电,2021(1):7-12. (SHU Jianguo, CHENG Changyong. Deep anti-sliding stability analysis of gravity dams based on FEM overload method[J]. Guangdong Water Resources and Hydropower, 2021(1): 7-12. (in Chinese) SHU Jianguo, CHENG Changyong. Deep anti-sliding stability analysis of gravity dams based on FEM overload method[J]. Guangdong Water Resources and Hydropower, 2021(1): 7-12. （in Chinese）
[5] 于沭, 陈祖煜, 王玉杰, 等. 用强度折减方法分析重力坝深层抗滑稳定性[J]. 水文地质工程地质,2009,36(3):64-70. (YU Shu, CHEN Zuyu, WANG Yujie, et al. Analysis on the deep anti-sliding stability of concrete gravity dam foundation by FLAC strength reduction method[J]. Hydrogeology & Engineering Geology, 2009, 36(3): 64-70. (in Chinese) doi: 10.3969/j.issn.1000-3665.2009.03.014 YU Shu, CHEN Zuyu, WANG Yujie, et al. Analysis on the deep anti-sliding stability of concrete gravity dam foundation by FLAC strength reduction method[J]. Hydrogeology & Engineering Geology, 2009, 36(3): 64-70. （in Chinese） doi: 10.3969/j.issn.1000-3665.2009.03.014
[6] 李征, 张林, 陈媛, 等. 复杂地基上重力坝的破坏过程及稳定安全度研究[J]. 中国农村水利水电,2016(2):130-133, 138. (LI Zheng, ZHANG Lin, CHEN Yuan, et al. Using different approaches to study the failure mode and stability of the gravity dam on complex foundation[J]. China Rural Water and Hydropower, 2016(2): 130-133, 138. (in Chinese) doi: 10.3969/j.issn.1007-2284.2016.02.033 LI Zheng, ZHANG Lin, CHEN Yuan, et al. Using different approaches to study the failure mode and stability of the gravity dam on complex foundation[J]. China Rural Water and Hydropower, 2016(2): 130-133, 138. （in Chinese） doi: 10.3969/j.issn.1007-2284.2016.02.033
[7] 王河, 王志鹏, 李永刚. 基于有限元超载-折减综合法的重力坝深层抗滑稳定性分析[J]. 水电能源科学,2016,34(2):65-68. (WANG He, WANG Zhipeng, LI Yonggang. Deep stability of gravity dam based on finite element synthetic method of strength reducing and overload[J]. Water Resources and Power, 2016, 34(2): 65-68. (in Chinese) WANG He, WANG Zhipeng, LI Yonggang. Deep stability of gravity dam based on finite element synthetic method of strength reducing and overload[J]. Water Resources and Power, 2016, 34(2): 65-68. （in Chinese）
[8] 周伟, 常晓林. 高混凝土重力坝复杂坝基稳定安全度及极限承载能力研究[J]. 岩土力学,2006,27(增刊1):161-166. (ZHOU Wei, CHANG Xiaolin. Study on stability safety and ultimate bearing capacity of complex dam foundation of high concrete gravity dam[J]. Rock and Soil Mechanics, 2006, 27(Suppl 1): 161-166. (in Chinese) ZHOU Wei, CHANG Xiaolin. Study on stability safety and ultimate bearing capacity of complex dam foundation of high concrete gravity dam[J]. Rock and Soil Mechanics, 2006, 27(Suppl 1): 161-166. （in Chinese）
[9] 苏培芳. 碾压混凝土重力坝安全度评价方法研究[J]. 人民长江,2012,43(2):78-82. (SU Peifang. Study on stability evaluation method for RCC gravity dam[J]. Yangtze River, 2012, 43(2): 78-82. (in Chinese) doi: 10.3969/j.issn.1001-4179.2012.02.018 SU Peifang. Study on stability evaluation method for RCC gravity dam[J]. Yangtze River, 2012, 43(2): 78-82. （in Chinese） doi: 10.3969/j.issn.1001-4179.2012.02.018
[10] 于建忠, 孙斌斌, 孙登峰, 等. 有限元超载法在拱坝整体安全分析中的应用[J]. 江苏水利,2019(2):28-31. (YU Jianzhong, SUN Binbin, SUN Dengfeng, et al. Application of finite element overloads method in the analysis of arch dam overall safety[J]. Jiangsu Water Resources, 2019(2): 28-31. (in Chinese) YU Jianzhong, SUN Binbin, SUN Dengfeng, et al. Application of finite element overloads method in the analysis of arch dam overall safety[J]. Jiangsu Water Resources, 2019(2): 28-31. （in Chinese）
[11] 陈胜宏. 计算岩体力学与工程[M]. 北京: 中国水利水电出版社, 2006. (CHEN Shenghong. Computational rock mechanics and engineering[M]. Beijing: China Water & Power Press, 2006. (in Chinese) CHEN Shenghong. Computational rock mechanics and engineering[M]. Beijing: China Water & Power Press, 2006. （in Chinese）
[12] 任威威, 苏超, 陈丽, 等. 某混凝土高拱坝整体安全度评估[J]. 水力发电,2012,38(4):21-23, 38. (REN Weiwei, SU Chao, CHEN Li, et al. Evaluation on overall safety degree of a high arch dam[J]. Water Power, 2012, 38(4): 21-23, 38. (in Chinese) doi: 10.3969/j.issn.0559-9342.2012.04.007 REN Weiwei, SU Chao, CHEN Li, et al. Evaluation on overall safety degree of a high arch dam[J]. Water Power, 2012, 38(4): 21-23, 38. （in Chinese） doi: 10.3969/j.issn.0559-9342.2012.04.007
[13] REN Q W, LI Q, JIANG Y Z, et al. Theory and methods of global stability analysis for high arch dam[J]. Science China Technological Sciences, 2011, 54(1): 9-17.
[14] 宋鹏, 程琳, 田振华. 高拱坝安全度计算方法对比分析[J]. 水力发电,2012,38(10):36-39, 52. (SONG Peng, CHENG Lin, TIAN Zhenhua. Comparative analysis on calculation methods of safety degree for high arch dam[J]. Water Power, 2012, 38(10): 36-39, 52. (in Chinese) doi: 10.3969/j.issn.0559-9342.2012.10.010 SONG Peng, CHENG Lin, TIAN Zhenhua. Comparative analysis on calculation methods of safety degree for high arch dam[J]. Water Power, 2012, 38(10): 36-39, 52. （in Chinese） doi: 10.3969/j.issn.0559-9342.2012.10.010
[15] 中华人民共和国水利部. 混凝土重力坝设计规范: SL 319—2018[S]. 北京: 中国水利水电出版社, 2018. (Ministry of Water Resources of the People’s Republic of China. Design specification for concrete gravity dams: SL 319—2018[S]. Beijing: China Water & Power Press, 2018. (in Chinese) Ministry of Water Resources of the People’s Republic of China. Design specification for concrete gravity dams: SL 319—2018[S]. Beijing: China Water & Power Press, 2018. （in Chinese）
[16] 蔡黎明, 孙琰. 浅谈对碾压混凝土重力坝失稳破坏机理的认识[J]. 科技与创新,2020(1):84-85. (CAI Liming, SUN Yan. Discussion on the understanding of instability and failure mechanism of RCC gravity dam[J]. Science and Technology & Innovation, 2020(1): 84-85. (in Chinese) CAI Liming, SUN Yan. Discussion on the understanding of instability and failure mechanism of RCC gravity dam[J]. Science and Technology & Innovation, 2020(1): 84-85. （in Chinese）
计量
- 文章访问数: 63
- HTML全文浏览量: 27
- PDF下载量: 31
