Email Alerts
RSS
Optimization of desilting construction scheme for pile foundation wharves considering structural safety
-
摘要:
中国沿海粉砂质海岸桩基码头下方普遍存在的严重泥沙回淤问题，导致码头桩基受损和高昂泥沙清淤成本。将桩基受力的有限元分析方法与港口运营管理的运筹学方法相结合，以大型沿海桩基码头泥沙清淤工程为原型，开展桩基码头的清淤施工方案优化研究，分别建立码头桩基-岸坡土体结构体系的有限元数值模型，以及综合考虑清淤成本、安全、效率的港口清淤施工方案优化数学模型，并应用基于强化学习改进的遗传算法求解得到最优清淤方案。方案在充分考虑结构安全的前提下，有效降低了清淤成本，可为港口清淤提供依据。
Abstract:The severe issue of sediment redeposition under pile foundation wharves along China’s silty coastal shores leads to damage to the pile foundations and high silt dredging costs. By integrating the finite element analysis method of pile foundation stress with operational research methods of port management, and taking large coastal pile foundation wharf silt dredging projects as prototypes, this study undertakes an optimization research on desilting construction strategies for pile foundation wharves. It establishes a finite element numerical model for the wharf pile foundation-slope soil structure system, as well as an optimization mathematical model for port dredging construction strategies that comprehensively considers dredging costs, safety, and efficiency. The optimal dredging scheme was obtained using a genetic algorithm improved by reinforcement learning (DDQN-GA). The scheme effectively reduces dredging costs while fully considering structural safety, providing scientifically sound and rational dredging project recommendations for port management.
-
高桩码头以其独特的适应性在中国沿海区域得到广泛应用，特别是在淤泥和粉砂质海岸区域的港口（如上海港、宁波港、天津港）。然而，因桩基应用环境恶劣及使用工况复杂，码头桩基的受损现象十分常见，其中不少是因码头下方泥沙回淤导致的桩基受损，这使得相应港口不得不定期进行清淤。桩基码头下方的清淤工程涉及面大，清淤成本高昂。因此，深入分析高桩码头的泥沙回淤问题，探讨有效的清淤施工方案，对降低清淤成本并保障码头的安全运营具有重要意义。对桩基受力特性的研究，Modak等[1]通过三维数值分析，评估了桩数、桩间距、桩长和桩径对黏土中大型桩筏基础沉降的影响，揭示了复杂的筏板-土壤-桩相互作用和荷载分担行为；Indraratna等[2]提出了一种新的离散元素-有限差分耦合方法，用于分析软土中单个石柱的荷载-变形行为，通过PFC2D和FLAC模拟石柱与周围黏土的相互作用，模型能够较好捕捉接触力分布和剪切应力轮廓；Souri等[3]使用大型离心机测试数据，评估了桩基码头数值模型和土壤本构模型的建模假设、方法及模型的适用性；Zhou等[4]研究发现预制混凝土桩与水泥土界面的摩擦能力显著依赖于水泥土的强度，并通过剪切试验分析了两者的关系。对清淤施工方案的研究主要有两类，一是基于泥沙回淤情况和环境条件建立模型，实现清淤工程的模拟和预测；二是综合考虑清淤工程和港口的运营情况建立模型以实现清淤工程方案的优化。前者如Dahl等[5]通过分析美国陆军工程兵团（USACE）提供的历史清淤费用数据，构建统计模型预测五大湖地区两个邻近大流域的淤泥量与其流域出口处的清淤成本；Williams[6]采用逐步线性回归技术开发预测模型，依据最低投标价格、政府成本估算和工程清淤量估计来预测工程的完工成本。后者如Kaizer等[7]开发了辅助港口清淤项目规划、组织、执行的计算模型，该模型可全面评估清淤效率和时效的影响因素，有助于降低成本并缩短清淤时间；Kaizer等[8]开发了港口清淤方案的优化模型，重点考虑清淤船舶的交通流量及多艘清淤船同时作业可能引起的相互干扰，从而实现对港口清淤活动的有效管理和优化；Souf Aljen等[9]开发了基于排队论的仿真程序，通过对港口吞吐量的模拟，进一步探讨了清淤作业对港口吞吐能力的影响；Mitchell等[10]开发了整数规划模型，探讨在固定总预算约束下，如何选择最优的维护性清淤项目；Tang等[11]提出了考虑清淤成本、通航安全性和效率的仿真优化框架，在有限清淤预算内综合优化航道尺寸。
但上述研究独立性较强，并没有建立系统性的框架来综合研究在泥沙回淤影响下桩基码头的结构安全和清淤施工方案的优化。本文在前人研究的基础上，综合考虑码头桩基受力特性、码头下方泥沙回淤、清淤工程成本优化等多个研究内容，通过基于实测数据构建的有限元模型，对桩基码头结构受力进行计算分析，在确保码头安全的前提下，以清淤工程的总成本最低为目标，构建码头清淤方案优化模型，最后通过基于强化学习改进的遗传算法进行模型求解。
1. 桩基码头清淤与结构安全
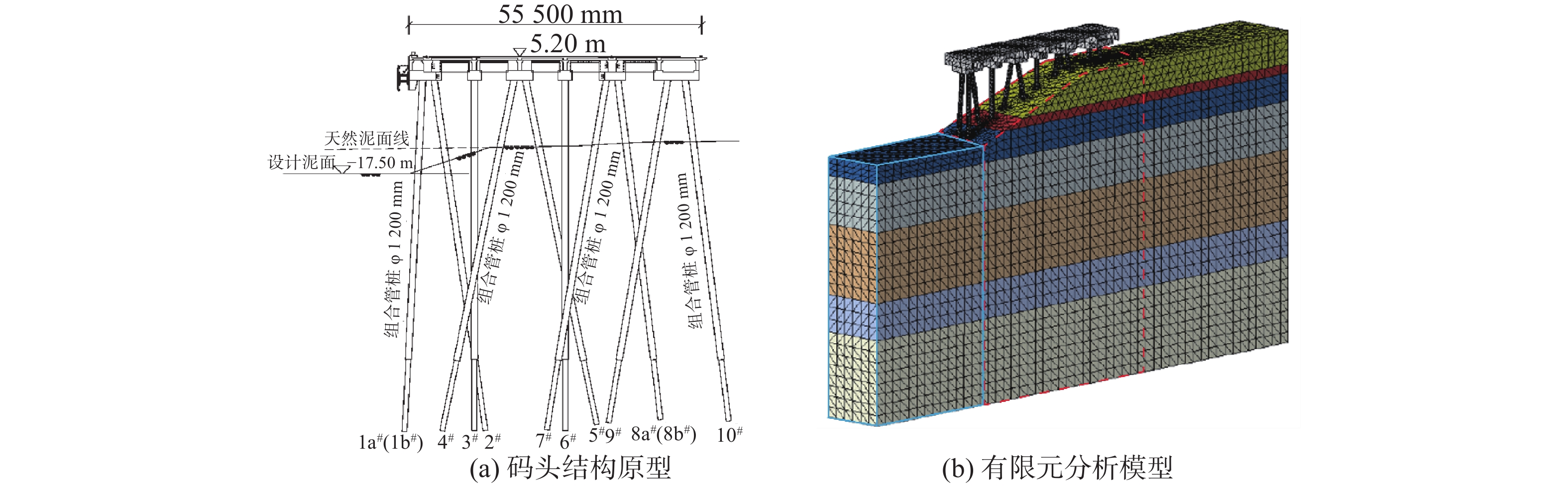
以某高桩码头为原型，其淤泥质海岸地区高桩码头总长1 500 m，包含3个10万t级集装箱泊位、1个7万t级集装箱泊位，码头顶面高程为5.20 m，前沿设计底高程为−17.50 m，码头宽55.5 m。码头结构采用高桩梁板式结构，排架间距10.5 m，上部结构均为现浇桩帽节点，预制横梁和纵向梁系，预制现浇叠合面板结构。排架结构及岸坡土体均使用改进的四面体单元C3D10M进行网格划分[12]。桩体和上部结构均为实体结构，采用线弹性模型[13] 。土体采用Mohr-Coulomb破坏准则的理想弹塑性模型[14]，在该模型中假定土体连续均匀，具有各向同性。土体的侧面在法向方向上受约束，底面在各个方向上均受约束。设置桩基与土体的接触对，其中强度较大的桩面设置为主面，强度较小的土体表面为从面。接触面的法向设置为“硬接触”，不可以互相穿透，切向允许滑动变形[4]。
现结合实测地质数据，选取其典型断面建立叉桩排架码头结构-地基土体有限元模型，开展泊位下方淤积高度对桩基受力特性影响的数值模拟。码头结构原型和有限元分析模型如图1所示，图1(b)中，实线框区域表示码头前沿，虚线框区域表示码头下方。
![]()
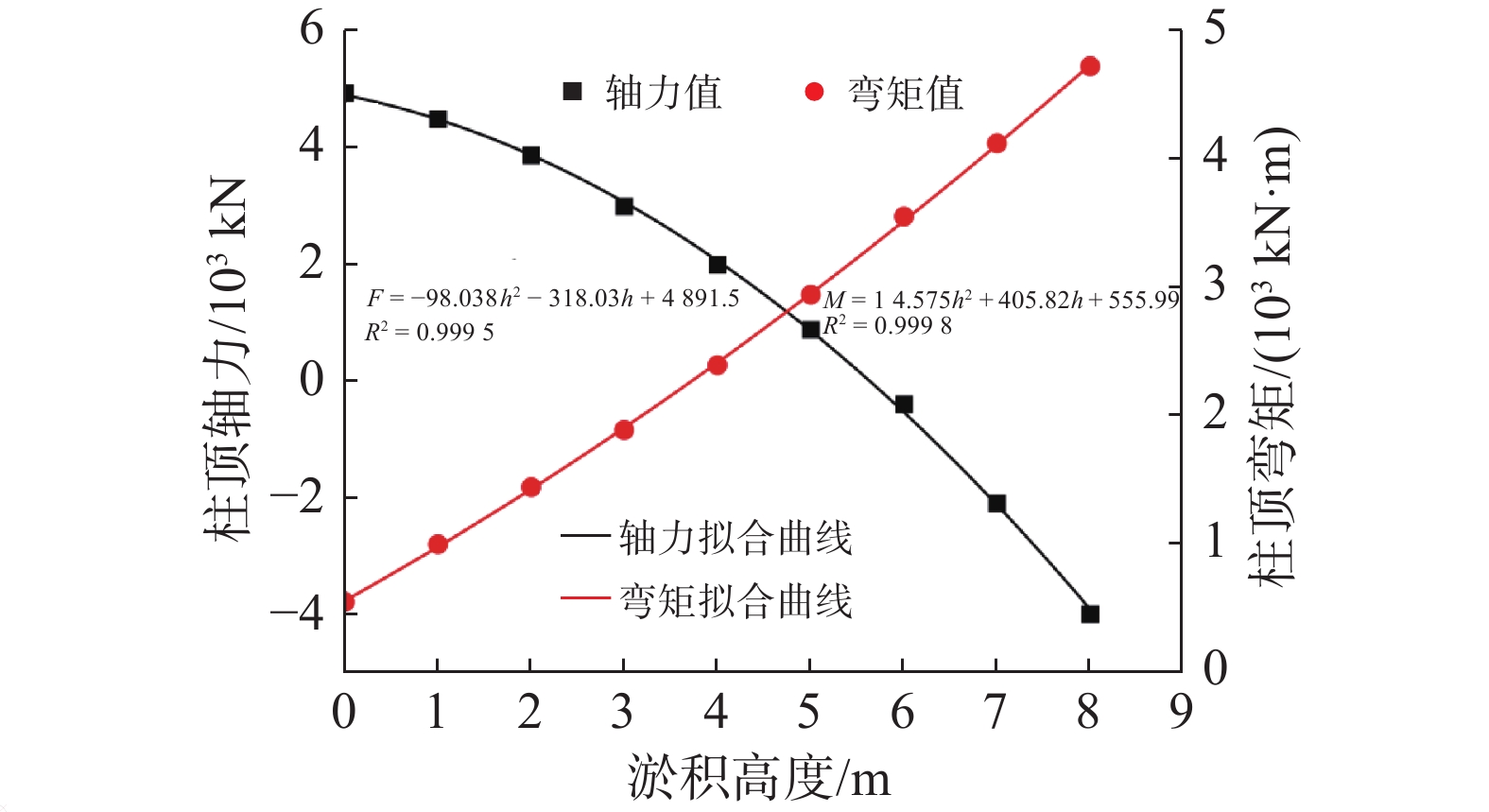
图 1 码头结构原型及其有限元分析模型Figure 1. Prototype of wharf structure and its finite element analysis model基于桩基受力特性影响机理分析，选取发生破损可能性最大的向岸侧桩基进一步开展定量分析，收集试验数据并建立淤积高度与桩顶轴力、桩顶弯矩的关系曲线（图2）。用二次函数拟合如下：
![]()
图 2 淤积高度与桩顶轴力、弯矩关系曲线Figure 2. Relationship curves between accumulation height and pile top axial force, bending moment$$ F=-98.038h^2-318.03h+4\ 891.5 $$ (1) $$ M = 14.575{h^2} + 405.82h + 555.99 $$ (2) 式中：F为不同淤积厚度下的轴力值(kN)；M为不同淤积厚度下的弯矩值（kN·m）；h为淤积厚度（m）。在预应力混凝土大管桩中，预应力钢束的张力大小、数量和分布形式都会影响管桩的抗弯承载力，进而影响其抗裂弯矩，同时轴力的大小也会影响管桩的受力状态和性能。在参考相关行业标准和研究文献[15-16]的基础上，得到码头下方广泛运用的1 200 mm预应力混凝土大管桩的抗裂弯矩$ {M}_{\mathrm{f}} $与轴力关系为：
$$ {M}_{\mathrm{f}}=0.24F+1\; 160 $$ (3) 结合式（1）~（3）和图2可以看出，在桩基码头下方淤积超过3 m后，其顶部实际弯矩值大于抗裂弯矩，将导致桩基码头结构顶部发生破损，这意味着该桩基码头有必要定期开展清淤工作，将码头下方的泥沙淤积控制在3 m以内，即清淤方案优化模型中的泥沙淤积厚度$ {H}_{\text{max}}^{1} $应设置为3 m。
2. 码头清淤方案优化模型
根据数值模拟的桩基码头安全运营的最大泥沙回淤厚度，并综合考量清淤工程中各类关键要素及成本，建立决策变量及目标函数，构建考虑桩基码头清淤工程总成本与结构安全的清淤方案优化模型。
码头泊位清淤需综合考虑码头运营安全、成本、工期等多方面因素。本文旨在制定出满足约束条件的泊位最优清淤方案，包括单次清淤深度、清淤频次、工期、清淤船型等要素。基于本文的工程背景，以泊位$ i $下方和前沿的第$ j $次清淤深度$ {h}_{ij}^{1} $和$ {h}_{ij}^{2} $、清淤船型$ {s}_{ij} $、清淤工程的开始时间$ {T}_{ij} $、清淤工程减少的工期时间$ {d}_{ij} $为决策变量。
清淤工程具有工程量大、成本高的特点，清淤工程占用泊位会导致码头工作能力下降，延长到港船舶的等待时间。因此，清淤工程的总成本应包括两个方面：清淤工程的直接工程成本$ {C}_{\mathrm{d}} $和清淤工程占用泊位带来的间接管理成本$ {C}_{\mathrm{r}} $。目标函数表示如下：
$$ f=\mathrm{min}({C}_{\mathrm{d}}+{C}_{\mathrm{r}}) $$ (4) （1）直接工程成本计算：根据产生工程成本的不同方式，清淤工程直接成本的计算可以概括为与工程量相关的可变成本$ {C}_{ij}^{\mathrm{v}} $、与清淤船型相关的固定成本$ {C}_{ij}^{\mathrm{f}} $及与工程工期相关的缩期成本$ {C}_{ij}^{\mathrm{s}} $的总和。
$$ {C}_{\mathrm{d}}=\displaystyle\sum _{i=1}^{{I}}\displaystyle\sum _{j=1}^{{J}}\left({C}_{ij}^{\mathrm{v}}+{C}_{ij}^{\mathrm{f}}+{C}_{ij}^{\mathrm{s}}\right) $$ (5) $$ C_{ij}^{\mathrm{v}}=Q_{ij}^1p_{ij}^1+Q_{ij}^2p_{ij}^2 $$ (6) $$ {C}_{ij}^{\mathrm{f}}=C\left({s}_{ij}\right) $$ (7) $$ {C}_{ij}^{\mathrm{s}}=\left({C}_{ij}^{\mathrm{v}}+{C}_{ij}^{\mathrm{f}}\right)({{d}_{ij}^{0}-{d}_{ij}})/{{d}_{ij}^{0}} $$ (8) 式中：I和J分别表示泊位总数和清淤工程开展的总次数；$ {Q}_{ij}^{1} $和$ {Q}_{ij}^{2} $分别表示泊位$ i $下方和前沿第$ j $次清淤的工程量；$ {p}_{ij}^{1} $和$ {p}_{ij}^{2} $分别表示泊位$ i $下方和前沿第$ j $次清淤的工程单价，$ p_{ij}=p_0(s_{ij})+\Delta h_{ij}k(s_{ij}) $，其中$ {p}_{0}({s}_{ij}) $表示使用船舶$ {s}_{ij} $时的基础挖深单价，$ k({s}_{ij}) $表示使用船舶$ {s}_{ij} $时的超挖单价系数，$ \Delta {h}_{ij} $表示泊位$ i $第$ j $次清淤工程的超挖深度，$ \Delta {h}_{ij}=\mathrm{max}(0,{h}_{ij}-{h}_{0}({s}_{ij})) $，其中${h}_{0}({s}_{ij} $)表示船舶$ {s}_{ij} $的基础挖深深度，$ {h}_{ij} $为泊位$ i $第$ j $次清淤工程的实际挖深深度，h0(Sij)表示泊位i第j次清淤工程中使用的清淤船舶Sij的基础挖深深度；$ {d}_{ij}^{0} $表示清淤工程的基本工期，是正常情况下清淤作业的最长工期，$ {d}_{ij} $表示在基本工期基础上减少的工期时间，$ {d}_{ij}^{0}=({{Q}_{ij}^{1}+{Q}_{ij}^{2}})/{\eta ({s}_{ij})} $，其中$ \eta ({s}_{ij}) $表示清淤作业效率。
（2）间接管理成本计算：清淤工程占用泊位产生的间接管理成本$ {C}_{\mathrm{r}} $包括两部分，一部分是疏浚船舶施工期间占用泊位，使码头整体服务能力下降，在船舶到达率不变的情况下会增加船舶等待时间成本$ {C}_{ij}^{\mathrm{w}} $；另一部分是泊位利用率下降带来的泊位使用成本$ {C}_{ij}^{\mathrm{b}} $。
$$ {C}_{\mathrm{r}}=\sum _{i=1}^{{I}}\sum _{j=1}^{{J}}\left({C}_{ij}^{\mathrm{w}}+{C}_{ij}^{\mathrm{b}}\right) $$ (9) $$ {W}_{ij}=\left({\dfrac{\rho }{1-\rho }-\dfrac{\left(N+1\right){\rho }^{N+1}}{1-{\rho }^{N+1}}}\right)/\left({u-\left(1-\dfrac{1-\rho }{1-{\rho }^{N+1}}\right)}\right) $$ (10) $$ {C}_{ij}^{\mathrm{w}}=\sum _{i=1}^{{I}}\sum _{j=1}^{{J}}\left(\Delta {W}_{ij}\times \lambda \times 24\times {d}_{ij}\times {c}^{\mathrm{w}}\right) $$ (11) $$ C_{ij}^{\mathrm{b}}=\sum_{i=1}^{{I}}\sum_{j=1}^{{J}}\left(c_i^{\mathrm{b}}d_{ij}\right) $$ (12) 式中：$ {W}_{ij} $为排队法计算得到的船舶平均等待时间[17]；$ \rho ={\lambda }/{\mu } $，$ \lambda $为船舶到达率，仅与季度相关，$ \mu $为泊位服务率，仅与泊位相关；N为当前可正常工作的泊位数量；$ \Delta {W}_{ij} $为$ {W}_{ij} $的增加量；$ {c}^{\mathrm{w}} $和$ {c}_{i}^{\mathrm{b}} $分别为船舶等待时间和泊位使用的单位成本。
泊位前沿及下方的回淤是一个长期的过程，开展清淤工程也对淤积高度产生直接影响，关注码头前沿及下方淤积高度的变化，建立针对码头前沿和下方淤积高度的安全约束：
$$ H\left(t\right)_i^1=H\left(0\right)_i^1+v_i^1t-\sum_{j=1}^{\mathrm{\it J}}h_{ij}^1x_{ij}\left(t\right)\leqslant H_{\mathrm{m}\mathrm{a}\mathrm{x}}^1 $$ (13) $$ H\left(t\right)_i^2=H\left(0\right)_i^2+v_i^2t-\sum_{j=1}^{\mathrm{\it J}}h_{ij}^2x_{ij}\left(t\right)\leqslant H_{\mathrm{m}\mathrm{a}\mathrm{x}}^2 $$ (14) $$ {x}_{ij}\left(t\right)=\left\{\begin{array}{c}0,\text{}t\leqslant {T}_{ij}\\ 1,\text{}t > {T}_{ij}\end{array}\right. $$ (15) 式中：$ H{\left(t\right)}_{i}^{1} $和$ H(t{)}_{i}^{2} $分别表示泊位$ i $下方和前沿在第t天的淤积高度，$ H{\left(0\right)}_{i}^{1} $和$ H{\left(0\right)}_{i}^{2} $分别表示泊位$ i $下方和前沿的初始淤积高度；$ {v}_{i}^{1} $和$ {v}_{i}^{2} $分别表示泊位$ i $下方和前沿的回淤速度；$ {h}_{ij}^{1}、{h}_{ij}^{2} $分别为泊位$ i $下方和前沿第$ j $次的清淤深度；$ {T}_{ij} $为泊位$ i $第$ j $次清淤工程的开始时间；$ {H}_{\text{max}}^{1} $为依据有限元分析结果进行计算的泊位下方桩基抗裂允许最大淤积高度；$ {H}_{\text{max}}^{2} $为根据泊位设计船型确定的泊位前沿允许最大淤积高度，泊位前沿淤积高度须低于$H_{{\text{max}}}^2$。
3. 基于DDQN-GA的算法设计
鉴于遗传算法具有并行处理、自适应进化、遗传信息不确定性及良好的兼容性等特点，本文选择遗传算法进行求解。但是，遗传算法在求解复杂问题时，也存在着局部搜索能力较弱、早熟收敛等问题。为此，又引入了DDQN (Double Deep Q-Network)来优化遗传算法，增强其局部搜索能力，在避免陷入局部最优的同时，加快收敛速度。
3.1 遗传算法
遗传算法是一种经典有效的优化算法，其核心内容主要包括种群编码方式、适应度函数及由选择、交叉、变异三部组成的种群更新方法。
3.1.1 编码方式
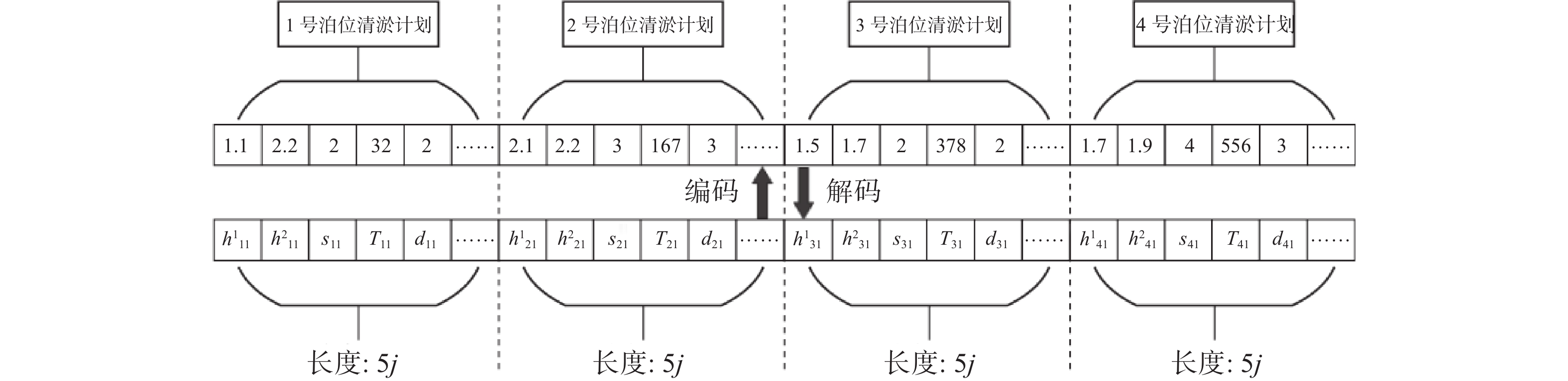
在考虑桩基码头清淤工程总成本与结构安全的清淤方案优化模型中，核心任务是为码头各个泊位制定满足约束条件下目标函数最小的清淤方案，在优化模型中，需要对i个泊位开展j次清淤工程，其中泊位数量固定为4，清淤工程次数j并不固定。因此将单个泊位的清淤方案（$ {h}_{ij}^{1} $、$ {h}_{ij}^{2} $、$ {s}_{ij} $、$ {T}_{ij} $、$ {d}_{ij} $）编码为1个基因，长度为5j，j为正整数，但值不固定，满足式（5）~（15）的约束条件即可。染色体由4个基因组成，交叉过程发生在不同染色体的相同位置的基因之间，同一个泊位的清淤方案相互交叉，变异过程针对单个基因进行，即重新生成单个泊位新的清淤方案。整个编码过程中采用实数编码的方式，种群中包含N个染色体，单个染色体编解码过程如图3所示。
3.1.2 适应度函数
本文优化模型的目标函数为最小化清淤工程总成本，将由式（4）计算得到的清淤工程总成本作为算法中的适应度函数，此时，种群中个体适应度的大小也反映着个体的优劣。
3.1.3 种群更新方式
遗传算法的种群通过选择、交叉、变异进行更新。选择操作分为以下三步：先计算种群中所有个体的适应度总和；再计算个体的被选择参数，对于每个个体，其选择参数大小等于该个体的适应度除以总适应度；最后，选择出个体参数大于交叉概率参数的个体，作为交叉种群。交叉操作主要发生在高适应度的种群间，先将选择操作确定的交叉个体两两分组作为父代个体，再选择父代个体同一位置的基因（同一泊位清淤方案）进行交换，产生新的子代个体（清淤方案）。
变异操作与适应度无关，所有个体都有相同概率发生变异。具体来说，变异过程先随机对每一个体都生成1个（0,1）区间内的随机数，然后选择出随机数小于变异概率参数的个体作为变异种群，变异种群将随机生成新的所有泊位的清淤计划。
3.2 强化学习
尽管通过遗传算法可以实现码头清淤方案的优化，但考虑到同一泊位前后清淤方案具有强关联性，不同泊位清淤方案也存在相互影响，且清淤次数不确定，仅使用遗传算法进行求解过于困难，遗传算法的变异操作很难进行有效扰动，算法易陷入局部最优。因此，本文采用DDQN方法对遗传算法的变异过程进行改进，通过定向变异实现有效全局扰动，使遗传算法能够更好更快地完成收敛。DDQN方法是DQN(Deep Q-Network)算法的改进版，通过两个神经网络使目标Q值的选择和目标Q值的计算进行解耦，有效解决了算法过拟合问题，同时加快了训练的收敛速度[18]。
本文将遗传算法的更新过程作为环境，通过与网络环境的交互实现模型训练，输出遗传算法的定向变异方案。DDQN与环境之间的交互过程可以用四元组S、A、R、γ表示，其中S表示状态，A表示动作，R表示奖励回报，γ为未来奖励的折扣因子。在参考其他文献[15-16]的基础上，结合本文研究的具体问题，给出如下的S、A、R的具体计算方法。
3.2.1 状态空间
状态空间S由4个连续实数组成，$ {S}_{1}、{S}_{2}、{S}_{3}、{S}_{4} $分别表示4个泊位的状态。令$ {\boldsymbol{Z}}_{it}^{1} $、$ {\boldsymbol{Z}}_{it}^{2} $分别表示第t次迭代后种群中所有个体在泊位$i$下方、前沿所有清淤工程清淤深度的集合；$ {\boldsymbol{Z}}_{it}^{\mathrm{c}} $表示第t次迭代后种群中所有个体对泊位$i$清淤的工程成本集合。每个泊位的状态都综合考虑了种群多样性和平均适应度，状态可以表示成如下形式：
$$ {S}_{i}=\sigma \left({\boldsymbol{Z}}_{it}^{1}\right)/\sigma \left({\boldsymbol{Z}}_{i0}^{1}\right)+\sigma \left({\boldsymbol{Z}}_{it}^{2}\right)/\sigma \left({\boldsymbol{Z}}_{i0}^{2}\right)+\sum \left({\boldsymbol{Z}}_{it}^{\mathrm{c}}\right)/\sum \left({\boldsymbol{Z}}_{i0}^{\mathrm{c}}\right),\quad i=\mathrm{1,2},\mathrm{3,4} $$ (16) 式中：$ \sigma $ 表示求集合的标准差；$ \sigma \left({\boldsymbol{Z}}_{it}^{1}\right)/\sigma \left({\boldsymbol{Z}}_{i0}^{1}\right)+\sigma \left({\boldsymbol{Z}}_{it}^{2}\right)/\sigma \left({\boldsymbol{Z}}_{i0}^{2}\right) $用以表示种群的多样性；$ \sum \left({\boldsymbol{Z}}_{it}^{\mathrm{c}}\right)/\sum \left({\boldsymbol{Z}}_{i0}^{\mathrm{c}}\right) $用以表示种群的平均适应度变化
3.2.2 动作空间
动作空间A由4个离散实数组成，$ {A}_{1}、{A}_{2}、{A}_{3}、{A}_{4} $分别表示4个泊位采取的动作，${A_i} \in \left[ {0,0.25,0.50} \right],i = 1,2,3,4$。令$ {T}_{\left(\mathrm{max},i\right)} $和$ {T}_{\left(\mathrm{min},i\right)} $分别表示泊位$i$单次清淤时间的上限和下限；令$ {h}_{\left(\mathrm{max},i\right)}^{1} $和$ {h}_{\left(\mathrm{min},i\right)}^{1} $分别表示泊位$i$的泊位下方单次清淤深度的上限和下限；令$ {h}_{\left(\mathrm{max},i\right)}^{2} $和$ {h}_{\left(\mathrm{min},i\right)}^{2} $分别表示泊位$i$的泊位前沿单次清淤深度的上限和下限。考虑到两次清淤工程间应间隔一定时间，同时为了减少清淤频次，单次清淤深度下限也应适当提升。因此，使用强化学习的动作调整清淤时间和清淤深度的下限，具体如下：
$$T_{(\min , i)}=\left\lceil T_{(\min , i)}+\left(T_{(\max , i)}-T_{(\min , i)}\right) \ A_i\right\rceil $$ (17) $$ {h}_{\left(\mathrm{min},i\right)}^{1}=\left\lceil {h}_{\left(\mathrm{min},i\right)}^{1}+\left({h}_{\left(\mathrm{max},i\right)}^{1}-{h}_{\left(\mathrm{min},i\right)}^{1}\right)\ {A}_{i}\right\rceil $$ (18) $$ {h}_{\left(\mathrm{min},i\right)}^{2}=\left\lceil {h}_{\left(\mathrm{min},i\right)}^{2}+\left({h}_{\left(\mathrm{max},i\right)}^{2}-{h}_{\left(\mathrm{min},i\right)}^{2}\right)\ {A}_{i}\right\rceil $$ (19) 式中：$\left\lceil \right\rceil$为向上取整操作，确保增加的下限值仍在合理范围内。
3.2.3 奖励回报
奖励回报$ R $为单个连续实数，令$ {\boldsymbol{C}}^{{t}} $表示t次迭代后种群中所有个体总成本的集合。本文使用强化学习优化遗传算法的目的是为了更好地指导遗传算法进行变异，取得更优的目标函数并提高收敛速度。因此，奖励函数综合考虑种群多样性变化和最优适应度变化，设置如下：
$$ r1=\left(\sigma \left({\boldsymbol{C}}^{{t}+1}\right)-\sigma \left({\boldsymbol{C}}^{{t}}\right)\right)/\sigma \left({\boldsymbol{C}}^{{t}}\right) $$ (20) $$ r2=\left(\text{min}\left({\boldsymbol{C}}^{{t}}\right)-\text{min}\left({\boldsymbol{C}}^{{t}+1}\right)\right)/\text{min}\left({\boldsymbol{C}}^{{t}}\right) $$ (21) $$ R=r1+r2 $$ (22) 3.3 基于DDQN-GA的优化算法
本文采用DDQN-GA的算法求解清淤优化方案问题，基于DDQN-GA优化算法框架，将遗传算法更新过程作为环境，首先观察当前环境状态，然后进行动作的选取并将动作应用到环境中，环境根据动作进行状态更新，并反馈更新后的状态、奖励等。DDQN通过与环境不断交互获得训练数据，对网络模型进行训练。
本文使用ε-greety策略进行动作${A_t}$的选择，具体选择方式如下：
$$ A_t=\left\{\begin{array}{ll}\text{argma}\text{x}_{\mathrm{a}}Q\left(\boldsymbol{S},\boldsymbol{A}\right), & P=1-\varepsilon_t \\ \mathrm{随}\mathrm{机}\mathrm{动}\mathrm{作,} & P=\varepsilon_t\end{array}\right. $$ (23) $$ {\varepsilon }_{t}={\varepsilon }_{t}\times \left(1-\delta \right) $$ (24) 式中：$ \text{argma}{\text{x}}_{{\mathrm{a}}}Q\left(\boldsymbol{S},\boldsymbol{A}\right) $表示依据策略a选择使$ Q\left(\boldsymbol{S},\boldsymbol{A}\right) $值最大的动作；$ {\varepsilon }_{t} $是一个介于0和1之间的参数，代表采取随机探索行为的概率；$ \delta $为衰减率。每次迭代后$ {\varepsilon }_{t} $都将通过式（24）进行更新。ε-greety动作选择策略能够引入随机性，以更好地探索环境并学到更多有用信息。在迭代初期，智能体对环境了解较少，此时较大的$ {\varepsilon }_{t} $能够帮助智能体更有效地进行探索。随着迭代推移，智能体对环境的了解增加，$ {\varepsilon }_{t} $不断减小，有助于智能体选择已知的高价值动作[19]。
DDQN通过当前的评价网络寻找具有最大Q值的动作，然后利用目标网络计算该动作的Q值，实现动作选择和动作评价的分离，从而有效缓解高估问题。DDQN的损失函数表示如下：
$$ L={\left(R+\gamma \widehat{Q}\left({\boldsymbol{S}}^{{'}},\text{argmax}\left(Q\left({\boldsymbol{S}}^{{'}},{\boldsymbol{A}}^{{'}}\right)\right);{\theta }^-\right)-Q\left(\boldsymbol{S},\boldsymbol{A};\theta \right)\right)}^{2} $$ (25) 式中：$ R+\gamma \widehat{Q}\left({\boldsymbol{S}}^{{'}},\text{argmax}\left(Q\left({\boldsymbol{S}}^{{'}},{\boldsymbol{A}}^{{'}}\right)\right);{\theta }^{-}\right) $为目标网络输出的目标值；$ Q\left(\boldsymbol{S},\boldsymbol{A};\theta \right) $为评价网络的估计值；$ \theta $和$ {\theta }^{-} $分别为评价网络和目标网络的网络参数。在计算得到网络损失后，网络通过Adam优化器，使用梯度下降方式完成网络的参数更新[19]。
4. 仿真结果与分析
4.1 实例数据
疏浚船型的选取是制定清淤方案的重要步骤，不同疏浚船型的基础挖深、疏浚单价、固定成本及施工效率等参数不同，依据工程实例和国家标准[20]，设置5种疏浚船型以供选取，具体参数如表1所示。
表 1 不同疏浚船型的清淤参数Table 1. Dredging parameters for different types of dredging ships疏浚船型 基础挖深/m 基础挖深单价/（元/m3） 超挖单价系数 其他固定成本/（万元） 工作效率/（万m3/d） A 10 5.72 0.11 14 1.9 B 10 5.65 0.11 13 1.8 C 9 5.58 0.11 12 1.7 D 8 5.55 0.11 11 1.6 E 8 5.51 0.11 10 1.5 依据码头设计资料，充分考虑清淤方案的成本和安全目标，优化模型中需要的泊位基础参数见表2。
表 2 桩基码头泊位相关参数Table 2. Relevant parameters of pile foundation wharf berths泊位编号 泊位长度/m 前沿清淤宽度/m 下方清淤宽度/m 船舶最大吃水/m 泊位管理成本/（万元/d） 平均服务时间/h 泊位1 330 45 55 13 5 15.5 泊位2 360 45 55 13 6 16.5 泊位3 450 45 55 13 6 16.5 泊位4 360 45 55 13 5 15.5 码头前沿设计底高程D为−17.50 m，依据相关标准和研究[21-22]，得到相应的码头前沿淤积限制高度：
$$ {H}_{\text{max}}^{2}=\left|D\right|-\alpha -\beta -\zeta$$ (26) 式中：$ \alpha $为靠泊船舶的最大吃水；$ \beta $为船舶龙骨下最小富裕深度，取0.5 m；$\zeta$为考虑各种因素的其他富裕深度，取0.5 m。根据式（26）可得码头前沿淤积高度限制$ {H}_{\text{max}}^{2} $为3.5 m。
根据码头的经营数据及船舶到达情况，船舶的到达过程为泊松分布[23]，考虑到不同季度港口泊位繁忙度存在差异，将全年的到达率分季度取值。参考港口泊位到达船型及同类研究对单位船舶的平均等待成本进行量化，第1、2、3、4季度的船舶平均达到时间$ 1/\lambda $分别为8.5、7.5、10.5、6.5 h，单位等待成本为1.25万元/h。依据泥沙回淤机理研究及码头实测底高程数据，将泊位前沿及下方初始淤积高度和不同季度回淤速率量化为具体的数值（表3）。
表 3 桩基码头回淤模型相关参数Table 3. Parameters related to the pile foundation wharf sedimentation model泊位编号 泊位前沿
初始淤高/m泊位下方
初始淤高/m泊位前沿夏秋季
回淤速率/(m/d)泊位前沿冬春季
回淤速率/(m/d)泊位下方夏秋季
回淤速率/(m/d)泊位下方冬春季
回淤速率/(m/d)泊位1 2.2 1.4 0.012 0.018 0.008 0.012 泊位2 2.4 1.5 0.013 0.019 0.009 0.013 泊位3 2.6 1.5 0.014 0.020 0.010 0.014 泊位4 2.7 1.6 0.015 0.021 0.011 0.015 基于上述实例数据开展试验研究，遗传算法参数设种群数N=100、交叉变异概率参数设置为0.6、0.4，迭代次数设置为500。DDQN的评价网络和目标网络均设为两层全连接层，折扣因子$ \gamma $设为1。ε-greety策略的初始$ {\varepsilon }_{t} $设为0.5，衰减率$ \delta $设为0.05。经验回放池的大小设置为100，学习率设置为0.001。
4.2 最优清淤方案
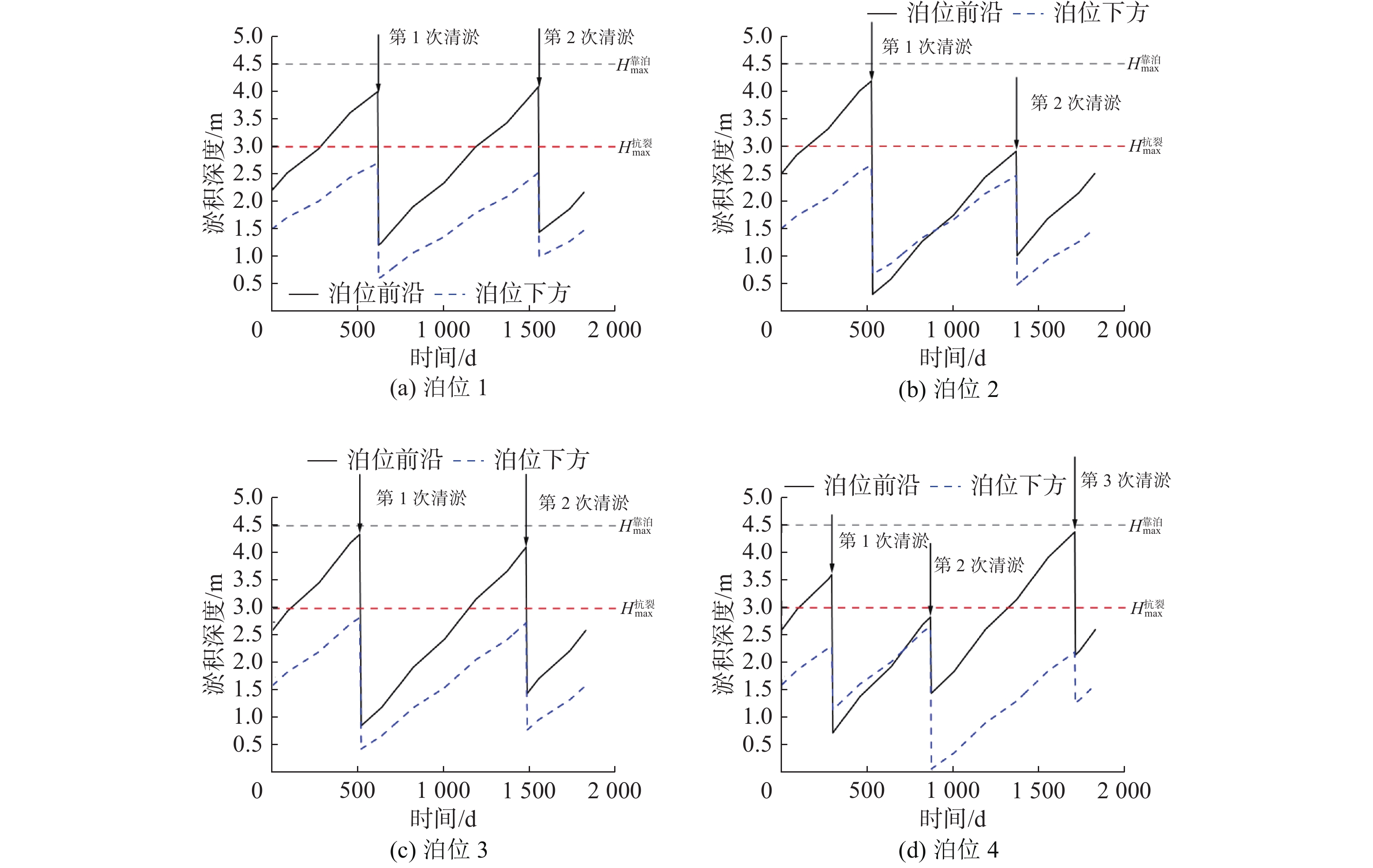
基于实例数据开展多次实验均在180次左右收敛，在最优清淤方案中，最低综合清淤成本为901.72万元、最优清淤方案下各个泊位参数变量的取值见表4（其中清淤工程以2019年1月1日作为记时起点）。依据求解结果，绘制计划期间内泊位下方、前沿的淤积高度变化线如图4所示。
表 4 桩基码头泊位清淤方案Table 4. Desilting scheme for pile foundation wharf berths泊位 清淤方案 下方清淤
深度/m前沿清淤
深度/m清淤船型 开始时间 工程工期/d 直接成本/万元 间接成本/万元 泊位1 第1次清淤 2.8 2.1 C 第618天 4 127.40 48.15 第2次清淤 2.7 1.5 A 第1 552天 4 泊位2 第1次清淤 3.9 2.0 B 第526天 6 142.13 67.87 第2次清淤 1.9 2.0 C 第1369天 4 泊位3 第1次清淤 3.5 2.4 C 第510天 7 191.46 83.10 第2次清淤 2.7 2.0 B 第1478天 5 泊位4 第1次清淤 2.9 1.2 C 第292天 5 170.68 70.93 第2次清淤 1.4 2.6 D 第866天 4 第3次清淤 2.2 0.9 A 第1706天 3 ![]()
图 4 桩基码头泊位前沿及下方淤积高度变化Figure 4. Changes in accumulation height in front of and below the pile foundation wharf berths由图4可见，计划期间泊位前沿和泊位下方淤积高度始终控制在安全范围以内，说明约束条件设置合理，清淤计划满足安全要求，实现了约束优化模型的安全目标。
在清淤计划制定及直接工程成本计算中，清淤工程开展次数和单次清淤深度高度相关，且这二者又存在明显的负相关关系，在回淤总量固定的情况下，应平衡好单次清淤深度与清淤次数的关系。根据试验求解结果，在计划期间（5年）每个泊位开展2~3次清淤工程较合适。
4.3 算法求解能力分析
为验证DDQN对GA算法定向变异改进的有效性，使用3组不同交叉变异概率参数的标准遗传算法进行对比，标准遗传算法的交叉概率参数依次设置为0.8、0.6、0.4，变异概率参数依次设置为0.2、0.4、0.6，迭代次数均设置为500，基于同样的实例数据进行运算，结果表明本文的DDQN-GA相比其他3种算法更快收敛，收敛结果也最优。将4种算法重复运行10次，目标函数最优值及收敛代数的对比结果见表5。结果再次表明DDQN-GA算法的可行性和优越性。
表 5 算法性能对比Table 5. Algorithm performance comparison算法 目标函数最优值/万元 收敛代数 最大值 最小值 平均值 标准差 最大值 最小值 平均值 标准差 SGA1 945.45 927.36 938.87 6.3 449 42 277 109.4 SGA2 939.51 926.78 934.34 4.3 469 69 252 136.1 SGA3 940.74 917.30 930.25 5.6 420 76 229 108.0 DDQN-GA 913.83 901.72 906.75 3.7 319 74 182 76.0 4.4 敏感性分析
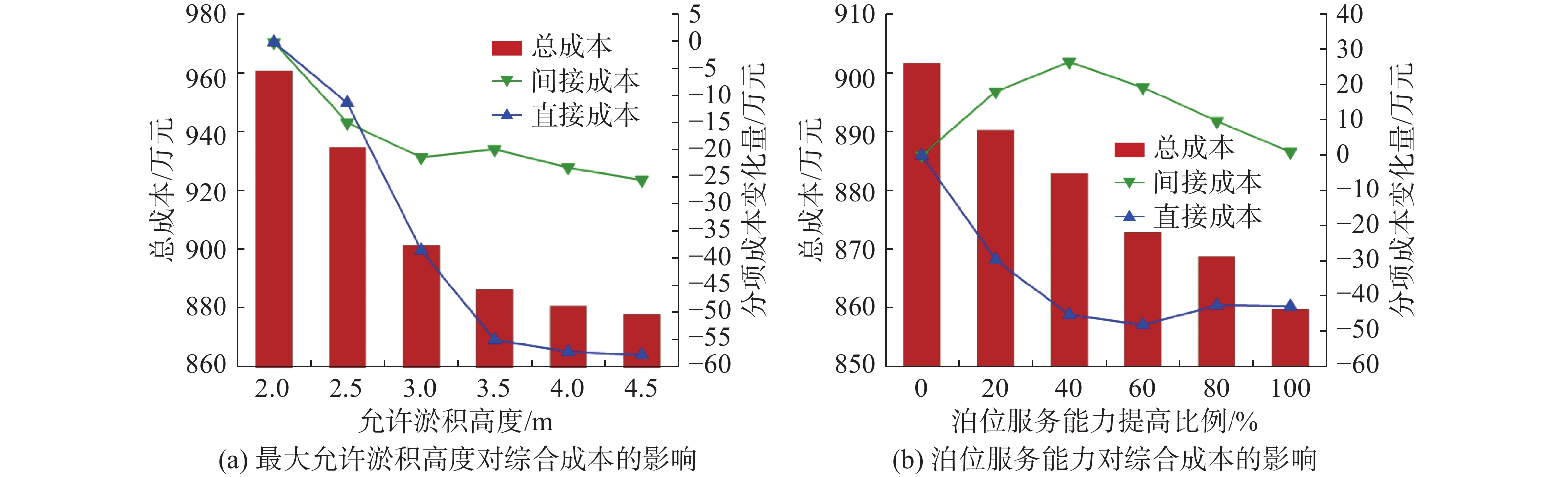
为分析桩基承载能力对清淤成本的影响，以泊位下方允许的最大淤积高度$ {H}_{\text{max}}^{2} $分别为3.00、3.25、3.50、3.75、4.00、4.25、4.50 m进行试验，并将成本绘制于图5(a)。
从图5(a)可以看出，随着$ {H}_{\text{max}}^{2} $的增加，清淤工程的总成本和直接成本都呈下降趋势。这主要是因为$ {H}_{\text{max}}^{2} $提高后，泊位下方淤积高度达到安全控制线的速度更慢，反映到清淤计划中，会减小清淤工程的频次，降低成本。此外，随着$ {H}_{\text{max}}^{2} $的增加，泊位下方单次清淤的超挖深度可能减少，清淤工程的直接成本也会进一步降低。虽然从整体趋势上看，清淤工程的总成本随着$ {H}_{\text{max}}^{2} $的增加而减少，但边际值逐渐下降，这主要是因为随着$ {H}_{\text{max}}^{2} $的提升，清淤的主要决定因素逐渐由单一的泊位下方淤积转至泊位前沿和泊位下方淤积。因此，为了最小化码头总成本，需综合考虑不同泊位下方允许最大淤积高度下的清淤成本和加固桩基的成本，在合适的时间加固桩基，提高桩基承载能力和最大允许淤积高度。
泊位服务能力是影响港口繁忙程度的重要参数，而清淤工程间接成本的核算与港口繁忙程度高度相关。为分析泊位服务能力对清淤成本的影响，将当前泊位服务能力分别提高5%、10%、15%、20%、25%、30%进行试验，并将成本绘制于图5(b)。
从图5(b)可以看出，随着泊位服务能力的提高，直接成本呈下降趋势，间接成本呈先升后降的趋势。在特定的清淤规划下，随着泊位服务能力的提升，船舶在港的平均等待时间会下降，清淤的直接成本不受影响，间接成本将会下降。这是因为缩短工期带来的成本降幅大于增加的间接成本。随着泊位服务能力的提升，清淤工程的总成本不断降低。因此，在综合考虑提升泊位服务能力成本和收益的基础上，适当提高泊位服务能力可降低清淤工程综合成本。
5. 结 语
因粉砂质海岸桩基码头下方普遍存在泥沙淤积，造成桩基受损及高昂的清淤成本问题，开展清淤施工方案优化研究，研究桩基码头清淤与结构安全的相关性，以泥沙淤积高度为自变量开展数值模拟试验，分析码头桩基受力特性的变化；基于第一层面的研究结论，结合成本目标和清淤工程中的各类参数变量，建立考虑桩基码头清淤工程总成本与结构安全的清淤计划优化模型，并设计基于强化学习改进的遗传算法求解模型，依据模型求解结果指导清淤计划的制定。
研究结果表明：码头下方的淤积厚度是影响码头安全营运及清淤成本的重要要素；清淤直接工程成本受到清淤次数和深度的影响，更少的单次清淤深度意味着更高频次的清淤，建议每个泊位5年内开展2~3次清淤；为实现清淤工程综合成本最小化的目标，可采取加固桩基方法，以提高桩基承载能力、泊位下方允许的最大淤积高度和泊位服务能力，从而弱化清淤工程对港口经营产生的影响。
-
![]()
图 1 码头结构原型及其有限元分析模型
Figure 1. Prototype of wharf structure and its finite element analysis model
![]()
图 2 淤积高度与桩顶轴力、弯矩关系曲线
Figure 2. Relationship curves between accumulation height and pile top axial force, bending moment
![]()
图 4 桩基码头泊位前沿及下方淤积高度变化
Figure 4. Changes in accumulation height in front of and below the pile foundation wharf berths
表 1 不同疏浚船型的清淤参数
Table 1 Dredging parameters for different types of dredging ships
疏浚船型 基础挖深/m 基础挖深单价/（元/m3） 超挖单价系数 其他固定成本/（万元） 工作效率/（万m3/d） A 10 5.72 0.11 14 1.9 B 10 5.65 0.11 13 1.8 C 9 5.58 0.11 12 1.7 D 8 5.55 0.11 11 1.6 E 8 5.51 0.11 10 1.5 
下载: 导出CSV
表 2 桩基码头泊位相关参数
Table 2 Relevant parameters of pile foundation wharf berths
泊位编号 泊位长度/m 前沿清淤宽度/m 下方清淤宽度/m 船舶最大吃水/m 泊位管理成本/（万元/d） 平均服务时间/h 泊位1 330 45 55 13 5 15.5 泊位2 360 45 55 13 6 16.5 泊位3 450 45 55 13 6 16.5 泊位4 360 45 55 13 5 15.5
下载: 导出CSV
表 3 桩基码头回淤模型相关参数
Table 3 Parameters related to the pile foundation wharf sedimentation model
泊位编号 泊位前沿
初始淤高/m泊位下方
初始淤高/m泊位前沿夏秋季
回淤速率/(m/d)泊位前沿冬春季
回淤速率/(m/d)泊位下方夏秋季
回淤速率/(m/d)泊位下方冬春季
回淤速率/(m/d)泊位1 2.2 1.4 0.012 0.018 0.008 0.012 泊位2 2.4 1.5 0.013 0.019 0.009 0.013 泊位3 2.6 1.5 0.014 0.020 0.010 0.014 泊位4 2.7 1.6 0.015 0.021 0.011 0.015
下载: 导出CSV
表 4 桩基码头泊位清淤方案
Table 4 Desilting scheme for pile foundation wharf berths
泊位 清淤方案 下方清淤
深度/m前沿清淤
深度/m清淤船型 开始时间 工程工期/d 直接成本/万元 间接成本/万元 泊位1 第1次清淤 2.8 2.1 C 第618天 4 127.40 48.15 第2次清淤 2.7 1.5 A 第1 552天 4 泊位2 第1次清淤 3.9 2.0 B 第526天 6 142.13 67.87 第2次清淤 1.9 2.0 C 第1369天 4 泊位3 第1次清淤 3.5 2.4 C 第510天 7 191.46 83.10 第2次清淤 2.7 2.0 B 第1478天 5 泊位4 第1次清淤 2.9 1.2 C 第292天 5 170.68 70.93 第2次清淤 1.4 2.6 D 第866天 4 第3次清淤 2.2 0.9 A 第1706天 3
下载: 导出CSV
表 5 算法性能对比
Table 5 Algorithm performance comparison
算法 目标函数最优值/万元 收敛代数 最大值 最小值 平均值 标准差 最大值 最小值 平均值 标准差 SGA1 945.45 927.36 938.87 6.3 449 42 277 109.4 SGA2 939.51 926.78 934.34 4.3 469 69 252 136.1 SGA3 940.74 917.30 930.25 5.6 420 76 229 108.0 DDQN-GA 913.83 901.72 906.75 3.7 319 74 182 76.0
下载: 导出CSV
-
[1] MODAK R, SINGH B. Numerical study on settlement-dependent variation of raft-soil-pile interactions for large piled raft in clay soil[J]. Ocean Engineering, 2023, 281: 115011. doi: 10.1016/j.oceaneng.2023.115011
[2] INDRARATNA B, NGO N T, RUJIKIATKAMJORN C, et al. Coupled discrete element-finite difference method for analysing the load-deformation behaviour of a single stone column in soft soil[J]. Computers and Geotechnics, 2015, 63: 267-278. doi: 10.1016/j.compgeo.2014.10.002
[3] SOURI M, KHOSRAVIFAR A, DICKENSON S, et al. Numerical modeling of a pile-supported wharf subjected to liquefaction-induced lateral ground deformations[J]. Computers and Geotechnics, 2023, 154: 105117. doi: 10.1016/j.compgeo.2022.105117
[4] ZHOU J J, YU J L, GONG X N, et al. The effect of cemented soil strength on the frictional capacity of precast concrete pile–cemented soil interface[J]. Acta Geotechnica, 2020, 15(11): 3271-3282. doi: 10.1007/s11440-020-00915-x
[5] DAHL T A, KENDALL A D, HYNDMAN D W. Impacts of projected climate change on sediment yield and dredging costs[J]. Hydrological Processes, 2018, 32(9): 1223-1234. doi: 10.1002/hyp.11486
[6] WILLIAMS T P. Modeling dredging project cost variations[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2003, 129(6): 279-285. doi: 10.1061/(ASCE)0733-950X(2003)129:6(279)
[7] KAIZER A, NEUMANN T. The model of support for the decision-making process, while organizing dredging works in the ports[J]. Energies, 2021, 14(9): 2706. doi: 10.3390/en14092706
[8] KAIZER A, SMOLAREK L. Methodology of creating a work schedule for dredging a port area[J]. Scientific Journals of the Maritime University of Szczecin, 2016, 45(117): 202-206.
[9] SOUF ALJEN A S, MAIMUN A, RAHIMUDDIN R, et al. Port capacity forecasting and the impact of the dredging works on port sea operations using discrete event simulation[J]. Journal Teknologi, 2016, 78(9-4): 31-40.
[10] MITCHELL K N, WANG B X, KHODAKARAMI M. Selection of dredging projects for maximizing waterway system performance[J]. Transportation Research Record: Journal of the Transportation Research Board, 2013, 2330(1): 39-46. doi: 10.3141/2330-06
[11] TANG G L, WANG W Y, GUO Z J, et al. Simulation-based optimization for generating the dimensions of a dredged coastal entrance channel[J]. Simulation, 2014, 90(9): 1059-1070. doi: 10.1177/0037549714540954
[12] EARIJ A, ALFANO G, CASHELL K, et al. Nonlinear three–dimensional finite–element modelling of reinforced–concrete beams: computational challenges and experimental validation[J]. Engineering Failure Analysis, 2017, 82: 92-115.
[13] ISBUGA V. Modeling of pile-soil-pile interaction in laterally loaded pile groups embedded in linear elastic soil layers[J]. Arabian Journal of Geosciences, 2020, 13: 1-17. doi: 10.1007/s12517-019-5007-7
[14] ZHAO L, CHENG X, DAN H, et al. Effect of the vertical earthquake component on permanent seismic displacement of soil slopes based on the nonlinear Mohr–Coulomb failure criterion[J]. Soils and Foundations, 2017, 57(2): 237-251. doi: 10.1016/j.sandf.2016.12.002
[15] 李荣庆, 侯永为. 考虑泥沙淤积影响的高桩码头三维有限元分析[J]. 水运工程,2016(10):95-99. (LI Rongqing, HOU Yongwei. Three-dimensional finite element analysis of pile-supported wharf considering sediment deposition[J]. Port & Waterway Engineering, 2016(10): 95-99. (in Chinese) doi: 10.3969/j.issn.1002-4972.2016.10.018 LI Rongqing, HOU Yongwei. Three-dimensional finite element analysis of pile-supported wharf considering sediment deposition[J]. Port & Waterway Engineering, 2016(10): 95-99. （in Chinese） doi: 10.3969/j.issn.1002-4972.2016.10.018
[16] 中华人民共和国交通运输部. 水运工程桩基设计规范: JTS 147-7—2022[S]. 北京: 人民交通出版社, 2023. (Ministry of Transport of the People’s Republic of China. Code for design of pile foundation on port and waterway engineering: JTS 147-7—2022[S]. Beijing: China Communications Press, 2023. (in Chinese) Ministry of Transport of the People’s Republic of China. Code for design of pile foundation on port and waterway engineering: JTS 147-7—2022[S]. Beijing: China Communications Press, 2023. （in Chinese）
[17] 何众颖. 基于排队论的岑港港区锚地需求计算与优化研究[D]. 舟山: 浙江海洋大学, 2019. (HE Zhongying. Research on calculation and optimization of anchorage demand in Cengang Port area based on queuing theory[D]. Zhoushan: Zhejiang Ocean University, 2019. (in Chinese) HE Zhongying. Research on calculation and optimization of anchorage demand in Cengang Port area based on queuing theory[D]. Zhoushan: Zhejiang Ocean University, 2019. （in Chinese）
[18] 朱雪琼, 胡成博, 杨景刚, 等. 基于DDQN的电力传感网资源分配算法[J]. 中国电力,2023,56(11):60-66. (ZHU Xueqiong, HU Chengbo, YANG Jinggang, et al. DDQN based resource allocation algorithm for power sensor networks[J]. Electric Power, 2023, 56(11): 60-66. (in Chinese) ZHU Xueqiong, HU Chengbo, YANG Jinggang, et al. DDQN based resource allocation algorithm for power sensor networks[J]. Electric Power, 2023, 56(11): 60-66. （in Chinese）
[19] CHEN R H, YANG B, LI S, et al. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem[J]. Computers & Industrial Engineering, 2020, 149: 106778.
[20] 中华人民共和国交通运输部. 疏浚工程船舶艘班费用定额: JTS/T 278-2—2019[S]. 北京: 人民交通出版社, 2019. (Ministry of Transport of the People’s Republic of China. Unit expense quota for ships of dredging engineering: JTS/T 278-2—2019[S]. Beijing: China Communications Press, 2019. (in Chinese) Ministry of Transport of the People’s Republic of China. Unit expense quota for ships of dredging engineering: JTS/T 278-2—2019[S]. Beijing: China Communications Press, 2019. （in Chinese）
[21] 中华人民共和国交通运输部. 河港工程总体设计规范: JTJ 212—2006[S]. 北京: 人民交通出版社, 2007. (Ministry of Transport of the People’s Republic of China. Code for master design of river port engineering: JTJ 212—2006[S]. Beijing: China Communications Press, 2007. (in Chinese) Ministry of Transport of the People’s Republic of China. Code for master design of river port engineering: JTJ 212—2006[S]. Beijing: China Communications Press, 2007. （in Chinese）
[22] 郭华. 乐山港老江坝作业区一期工程通航水流条件及泥沙淤积研究[D]. 重庆: 重庆交通大学, 2012. (GUO Hua. Study on navigable flow conditions and sediment deposition of the first phase project of Laojiangba operation area in Leshan Port[D]. Chongqing: Chongqing Jiaotong University, 2012. (in Chinese) GUO Hua. Study on navigable flow conditions and sediment deposition of the first phase project of Laojiangba operation area in Leshan Port[D]. Chongqing: Chongqing Jiaotong University, 2012. （in Chinese）
[23] 张怀慧, 蒋大煌. 船舶到港分布律的研究及合理泊位数的计算[J]. 水运工程,2014(9):51-56. (ZHANG Huaihui, JIANG Dahuang. Distribution law of ships to port and calculation of reasonable number of berths[J]. Port & Waterway Engineering, 2014(9): 51-56. (in Chinese) doi: 10.3969/j.issn.1002-4972.2014.09.010 ZHANG Huaihui, JIANG Dahuang. Distribution law of ships to port and calculation of reasonable number of berths[J]. Port & Waterway Engineering, 2014(9): 51-56. （in Chinese） doi: 10.3969/j.issn.1002-4972.2014.09.010
计量
- 文章访问数: 118
- HTML全文浏览量: 43
- PDF下载量: 32
